1. Множини, їх види, операції над множинами та їх властивості. Числові множини. Точна верхня і точна нижні межі множин

Під множиною розуміється будь-яка сукупність об’єктів, що називаються елементами множини, об’єднаних за якоюсь ознакою.

Запис означає, що об’єкт є елементом множини (належить множині А), у противному випадку .

Види множин:

1. Множина що не містить жодного елемента називається порожньою і позначається .

2. Запис (А міститься в В) означає, що кожний елемент множини А є елементом множини В, у цьому випадку множина А називається підмножиною множини В.

3.Множини А і В рівними (А = В), якщо і .

4. Якщо підмножина деякої універсальної множини , то різниця позначається і називається доповненням множини (до множини Е)

5. Розглядаються множини елементи яких містяться в деяких фіксованих множинах (лін простори, дійсні числа). Така множина називається універсальною

6. За кількістю елементів:

а) скінченні,

б) нескінченні (зчисленні і незчисленні)

Існують два основних задання множини:

1. множина А визначається безпосереднім перерахуванням всіх елементів , тобто записується у вигляді

2. множина А визначається як сукупність тих і тільки тих елементів із деякої основної (універсальної) множини Е, які мають загальну властивість . У цьому випадку використовується позначення де запис означає, що елемент 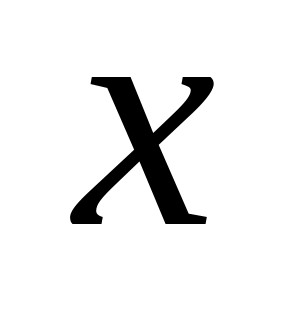має властивість .

Операції над множинами

1. Об’єднання. Об’єднанням множин А і В називається множина

2. Перетином множин А і В називається множина

3. Різницею множин А і В називається множина

4. Прямим або декартовим добутком множин А і В називається множина

Властивості операцій над множинами

1. комутативність операції і

2. асоціативність

3. дистрибутивність

4. закони двоїстості

5.

6.

Операції і природно узагальнюються на випадок довільної сім’ї множин. Нехай, наприклад, задана сім’я множин , , де I – індексна (скінченна або нескінченна) множина. Тоді визначимо і

Числові множини – множини, елементами яких є числа:

1. Множина натуральних чисел

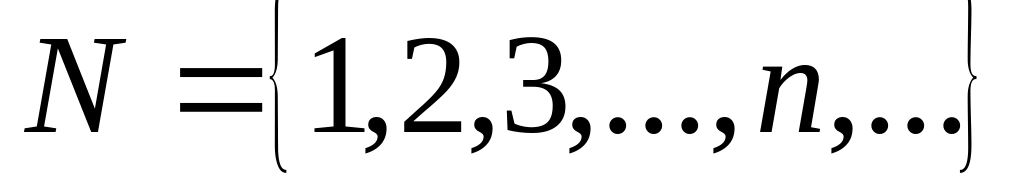
2. Множина цілих чисел

– множина цілих додатних чисел.

3. Множина раціональних чисел , де – ціле число, ; – натуральне число, .

Між цими множинами існує зв'язок

4. Множина ірраціональних чисел:

Множина раціональних чисел разом з множиною ірраціональних чисел утворюють множину дійсних чисел R

5. Множина комплексних чисел С.

Точна верхня і точна нижня межі множини

Виз. Множина М обмежена зверху Число с називається верхньою межею множини М.

Виз. Найменша серед усіх верхніх меж обмеженої зверху множини називається точною верхньою межею. Позначення: . Інакше кажучи:

Умова 1) означає, що – верхня межа, а умова 2) означає, що – найменша з усіх верхніх меж.

Або на мові епсілон :

Виз. Множина М – обмежена знизу с називається нижньою межею множини М.

Виз. – найбільша серед усіх нижніх меж, тобто

Або на мові епсілон:

Якщо , то кажуть, що супремум досягається і пишуть . Якщо інфімум досягається і .

Th: всяка обмежена зверху (знизу) числова множина має точну верхню (нижню) грань.

Виз. необмеж. Зверху

Виз. необмеж. Знизу