
- •2) Электростатическое поле и его силовые характеристики.
- •3) Поток напряженности электрического поля
- •2) Потенциал и его связь с напряженностью электростатического поля.
- •3) Основные уравнения электростатики.
- •6) Проводники в электрическом поле.
- •7) Энергия электрического поля в конденсаторе.
- •6) Закон Джоуля-Ленца в дифференциальной и интегральной форме.
- •7) Правило Кирхгофа.
- •2) Закон Био-Савара-Лапласа.
- •2) Намагниченность.
- •3) Магнитные восприимчивость и проницаемость.
- •4) Температура Кюри. Домены.
- •5) Магнетизм горных пород. Палеомагнетизм.
- •5) Индуктивность длинного соленоида и Энергия магнитного поля.
- •6) Взаимоиндукция
- •7) Трансформация токов и напряжений.
- •8) Сейсмографы.
- •3) Мощность переменного тока.
- •2) Дифференциальное уравнение собственных электромагнитных колебаний в контуре.
- •3) Затухающие колебания.
- •2) Основные положения теории Максвелла.
- •3) Вихревое электрическое и потенциальное магнитное поле.
- •5) Уравнения Максвелла в интегральной форме.
- •6) Электромагнитные волны и их свойства.
- •7) Шкала электромагнитных волн.
- •2) Излучение и поглощение света.
- •3) Спектры. Основы спектрального анализа.
- •8) Принцип действия лазера.
- •4) Распределение интенсивности света в интерференционном поле.
- •5) Интерференция в тонких пластинах. Интерферометры.
- •2) Принцип Гюйгенса-Френеля.
- •3) Дифракция Френеля и Фраунгофера.
- •4) Дифракционная решетка.
- •5) Дифракционные спектры и спектрографы.
- •6) Дифракция рентгеновских лучей в кристаллах.
- •7) Формула Вульфа-Брэггов.
- •2) Закон Малюса. Закон Брюстера.
- •3) Двойное лучепреломление в одноосных кристаллах.
- •4) Вращение плоскости поляризации.
- •5) Методы поляризационного анализа горных пород.
- •6) Нормальная и аномальная дисперсия света.
- •4) Гипотеза де Бройля.
- •6) Квантовые числа.
- •9) Энергия связи нуклонов в ядре и дефект массы.
- •10) Взаимные превращения нуклонов.
- •13) Термоядерный синтез и проблема управляемых термоядерных реакций.
3) Вихревое электрическое и потенциальное магнитное поле.
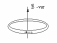
Пусть
какой-либо проводящий контур находится
в меняющемся со временем магнитном поле
и равен
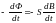 .
(S-const)
.
(S-const)
В проводнике в этом случае существует электрическое поле, вызывающее движение электрических зарядов, т.е. индукционный ток. Гипотеза Дж.Максвелла предполагает, что электрическое поле возникает в пространстве при изменении магнитного поля независимо от того, расположен ли в этом месте проводник или его нет. Наличие проводника лишь позволяет убедиться в существовании такого электрического поля.
Постоянное магнитное поле (поле постоянных токов, текущих по неподвижным относительно друг друга проводникам, или поле неподвижных относительно друг друга магнитов) действует только на токи, но на неподвижные заряды не влияет. Но меняющееся со временем магнитное поле создает электрическое поле, действующее и на неподвижные заряды
Электрическое поле, возникающее в пространстве, где есть меняющееся магнитное поле, существенно отличается от электростатического поля:
оно не связано с наличием электрических зарядов;
линии вектора напряженности в нем замкнуты;
циркуляция вектора напряженности по замкнутому контуру не равна нулю, т.е.
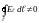 (для электростатического
поля
(для электростатического
поля
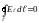 во всех случаях).
во всех случаях).
Покажем, что , если контур пересекается переменным магнитным полем.
Разность
потенциалов V1
- V2
между двумя точками поля связана с
напряженностью поля: V1
- V2
=
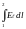 .
.
 Если
интеграл распространить на весь контур,
то вместо V1
- V2
надо ввести
ЭДС индукции: и
=
Если
интеграл распространить на весь контур,
то вместо V1
- V2
надо ввести
ЭДС индукции: и
=
 ,
но и
= -
,
но и
= -
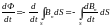 ,
т.о.
,
т.о.
=
-
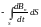 .
Если
.
Если
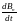
0, то
.
Это означает, что возникающее электрическое
поле вихревое.
0, то
.
Это означает, что возникающее электрическое
поле вихревое.
4) Ток смещения
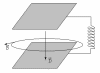
Токи проводимости на всех участках цепи, где они существуют, создают магнитное поле. При изменении электрического поля в конденсаторе также возникает магнитное поле. Оно ничем не отличается от поля, создаваемого токами проводимости. Дж.Максвелл предложил считать, что в конденсаторе существует особый вид электрического тока, не связанный с направленным перемещением заряда, и предложил называть его током смещения. Ток смещения существует между пластинами конденсатора и тогда, когда между ними нет диэлектрика (вакуумный конденсатор), он не сопровождается выделение тепла.
Если сила тока проводимости определяется зарядом, проходящим в секунду через поперечное сечение проводника: I проводимости = , где dQ заряд, проходящий через поперечное сечение проводника за время dt. Аналогично сила тока смещения определяется той же формулой: I смещения = , но в этом случае dQ - изменение заряда конденсатора за время dt.
Поскольку
Q
= CU,
где U
- напряжение на конденсаторе емкости
C,
то dQ
= C
dU,
но для
однородного поля между пластинами
конденсатора
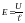 ,
где
,
где
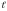 -
расстояние между пластинами конденсатора,
отсюда dU
=
-
расстояние между пластинами конденсатора,
отсюда dU
=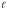 dE,
тогда dQ
= C
dE.
Ток смещения в этом случае определится
как I
смещения
=
=
С
dE,
тогда dQ
= C
dE.
Ток смещения в этом случае определится
как I
смещения
=
=
С
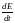 (Обратите внимание: ток проводимости
пропорционален напряженности
электрического поля I
проводимости,
= SE,
то ток смещения
пропорционален первой производной от
напряженности электрического поля по
времени)
(Обратите внимание: ток проводимости
пропорционален напряженности
электрического поля I
проводимости,
= SE,
то ток смещения
пропорционален первой производной от
напряженности электрического поля по
времени)
Преобразуем
полученную формулу, учитывая, что для
плоского конденсатора
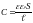 ,
электрическое смещение D
= -E,
поток вектора электрического смещения
=DS,
тогда имеем
I
смещения
=
=
С
=
,
электрическое смещение D
= -E,
поток вектора электрического смещения
=DS,
тогда имеем
I
смещения
=
=
С
=
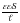 =
=
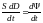 ,
т.е. сила тока смещения пропорциональна
скорости изменения потока вектора
электрического смещения.
,
т.е. сила тока смещения пропорциональна
скорости изменения потока вектора
электрического смещения.
В конденсаторе колебательного контура ток смещения достигает наибольшего значения в те моменты, когда напряжение на конденсаторе и поток вектора электрического смешения равны нулю. В этот момент и ток проводимости в подводящих проводах имеет максимальное значение.
Дж.Максвелл ввел понятие полного тока, плотность которого определяется геометрической суммой плотностей тока проводимости и тока смещения. Полный ток в цепи всегда замкнут.
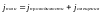 где
где
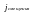 =
=
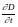
Теорема о циркуляции вектора напряженности магнитного пля по замкнутому контурку с учетом полного тока должна быть записана в виде:
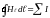 ,
т.е.
,
т.е.
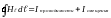 или
или
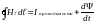 .
.
Ток смещения имеется всюду, где есть меняющееся электрическое поле, следовательно, он существует и в проводниках, по которым течет переменный электрический ток (при не очень высоких частотах ток смещения мал по сравнению с током проводимости).
