3) Затухающие колебания.

Любая реальная электрическая цепь обладает активным (омическим) сопротивлением (R  0). В таком контуре энергия электрического и магнитного поля постепенно убывают за счет перехода в тепло – колебания затухают.

Можно получить уравнения, описывающие процессы в контуре на основе закона сохранения энергии: тепло в активном сопротивлении образуется за счет уменьшения энергии электрического поля в конденсаторе и энергии магнитного поля в катушке.

dW_R + dW_L + dW_C = 0 (сумма всех изменений энергии равна нулю).

Энергия электрического поля W_C = , изменение энергии dW_C;= ;

энергия магнитного поля W_L, =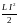 , изменение энергии dW_L = ;

тепловая энергия W_R = I² R t, изменение энергии dW_R = I² R dt.

I² R dt + + = 0 или + I² R + 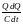=0. Учитывая, что =I, можно провести сокращение. Оставив первое слагаемое без множителя и введя обозначения: Q’’ = , Q’= I = , , , получим дифференциальное уравнение для затухающих колебаний в стандартной форме записи:

Q’’ + 2 Q’+ ₀³ Q = 0. решение которого Q = Q₀ e ^{-  t} sin( t + ),

где  = = .

Как и для механических колебаний:

0. показатель затухания  = , где  - время релаксации, т.е. время, за которое амплитуда колебаний убывает в е раз;

1. логарифмический декремент затуханий  = , где N - число колебаний, за которые амплитуда убывает в е раз;

4) Добротность контура.

Добротность контура – характеризует качество колебательного контура, обозначается Q. Определяется как отношение реактивной энергии в колебательной системе - колебательном контуре к энергии активных потерь в нем за период колебаний.

Понятие добротности Q колебательной системы определяется по формуле:

где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

Для RLC-контура добротность Q выражается формулой

5) Вынужденные колебания.

Если оказывать на контур внешние периодические воздействия, подзаряжая конденсатор, то колебания в контуре не будут затухать. Такие колебания в контуре с активным сопротивлением называют вынужденными. Осуществить это можно несколькими способами, например:

1. включив параллельно с конденсатором источник переменной ЭДС;

2. включив последовательно с другими элементами контура источник переменной ЭДС.

В обоих случаях за счет работы сторонних сил происходит восполнение энергии колебательного контура. В соответствии с законом сохранения энергии:

dW_ист = dW_L + dW_R + dW_C . После подстановки значений получаем уравнение:

. После введения стандартных обозначений получаем дифференциальное уравнение:: Q’’ + 2Q’ + _oQ = sin  t, решение которого состоит из двух частей:

первое слагаемое Q₀ e ^-t sin ( t + ) содержит экспоненциальный множитель и быстро убывает со временем (если не рассматривать начало процессов в контуре, это слагаемое можно не учитывать);

второе слагаемое Q = А sin ( t + ), где А = Q_A = 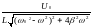и

tg  = . Подставляя и , имеем tg  = .

А = .

Ток в контуре можно определить, дифференцируя заряд конденсатора по времени. Амплитудное значение силы тока:

I₀ = 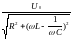, где L - индуктивное сопротивление:

емкостное сопротивление;

К - активное сопротивление.

- полное сопротивление.

6) Резонанс напряжений и токов.

Резонанс

При приближении частоты вынужденных колебаний к частоте собственных колебаний контура _o резко возрастает амплитуда колебаний. Это явление называют резонансом

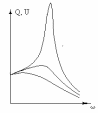
Резонансная частота для заряда Q и напряжения на конденсаторе U определяется при исследовании на экстремум амплитуды:

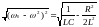
_р =  _о

При _о=0 резонансные кривые сходятся в точке, соответствующей напряжению (соответственно заряду) на пластинах конденсатора при подключении к нему источника постоянного напряжения U₀. При уменьшении  максимум становится более резким. При 0 _р_о.

Резонансные кривые силы тока имеют иную форму, что связано с тем, что резонансное значение силы тока независимо от  достигается при _р = _о.

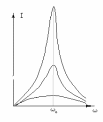
Действительно, поскольку I₀ = , то максимум тока достигается при 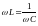, т.е. _р = _о.

Резонанс напряжений

В цепи, изображенной на схеме, при резонансной частоте изменения тока и напряжения происходят синфазно. При этом падение напряжения на конденсаторе и катушке индуктивности авны и противоположны по фазе. В этом случае падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи. Это явление называется резонансом напряжений.

При резонансе напряжений сопротивление цепи оказывается чисто активным и имеет наименьшее значение при данных параметрах цепи.

Резонанс токов

Если цепь с пренебрежимо малым активным сопротивлением собрана по схеме, приведенной на рисунке, то при резонансной частоте токи на участке конденсатора и катушки индуктивности могут быть очень велики, но они противоположны по фазе, поэтому ток в подводящих проводах близок к нулю. Это явление называют резонансом токов.

При резонансе токов сопротивление цепи чисто активное и имеет наибольшее значение при данных параметрах.

10.Электромагнитное поле. Основные положения теории Максвелла. Вихревое электрическое и потенциальное магнитное поле. Ток смещения. Уравнения Максвелла в интегральной форме. Электромагнитные волны и их свойства. Шкала электромагнитных волн.

1) Электромагнитное поле.

Электромагнитное поле - это особая форма материи, посредством которой осуществляется взаимодействие между заряженными частицами. Представляет собой взаимосвязан­ные переменные электрическое поле и магнитное поле. Взаимная связь электрического Е и магнитного Н полей заключается в том, что всякое изменение одного из них приводит к появ­лению другого: переменное электрическое поле, порождаемое уско­ренно движущимися зарядами (источником), возбуждает в смежных областях пространства переменное магнитное поле, которое, в свою очередь, возбуждает в прилегающих к нему областях пространства переменное электрическое поле, и т. д. Таким образом, электромагнитное поле распространяется от точки к точке простран­ства в виде электромагнитных волн, бегущих от источника. Благодаря конечности скорости распространения электромагнитное поле может существовать автономно от породившего его источ­ника и не исчезает с устранением источника (например, радио­волны не исчезают с прекращением тока в излучившей их антенне).

Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла.