Раздел 1. Встроенные функции.

Для построения графика данной функции на заданном отрезке с интервалом 0,1 нужно построить таблицу значений X и Y на этом интервале. Я ввожу начальное значение Х=0 в ячейку A3. В ячейку А4 ввожу формулу «=А3+0,1» . . В ячейку B3 ввожу формулу «=ЕСЛИ(A3<0,4;ASIN((A3)^2+0,1);ЕСЛИ(A3>0,6;COS(A3+0,5)/SIN(A3+0,5);EXP(A3+1)))»

Копирую ячейки A4 и B3 пока в столбце А не получится число 1.

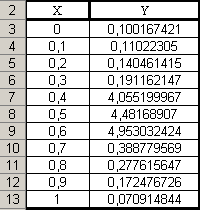
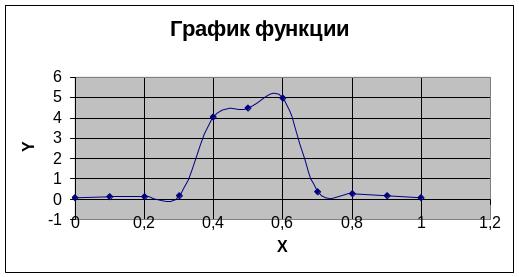
Дальше выделяю полученную таблицу, выбираю «мастер диаграмм» и строю точечную диаграмму со значениями, соединёнными сглаживающими линиями, без легенды.

Раздел 2. Поиск корней нелинейных уравнений.

Построим таблицу значений X и Y , повторив действия, описанные в первом задании.

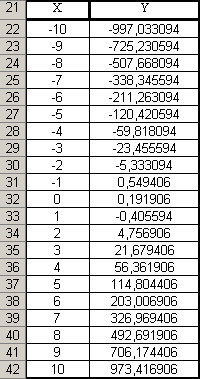
Значение Y вычисляется по формуле

«=A22^3-0,12*A22^2-1,4775*A22+0,191906»

Аналогично первому заданию строю график функции на заданном интервале.

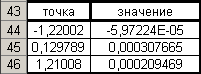
По графику видны точки близкие к 0. Это точки -5, 0 и 5. Ввожу в ячейки А44-А46 значения -5, 0 и 5 соответственно. Далее выбираю Сервис – подбор параметра.

Установить в ячейке: В44

Значение: 0

Изменяя значение ячейки: А44

Аналогично подбираю значение Х для двух других точек.

Результат:

Раздел 3. Операции над матрицами.

Для ввода матрицы А я выделяю ячейки B50-G55, ввожу « ={1;-5;3;-5;-1;-3:4;0;3;3;2;3:3;0;3;1;0;4:-5;0;0;3;-5;-2:-2;-4;-3;-1;-1;2:-4;-2;2;0;-2;-4}» и нажимаю Shift+Ctrl+Enter.

Для того, чтобы найти обратную матрицу, я выделяю столько же ячеек, сколько в данной матрице, ввожу строку «=МОБР(matrica)» и нажимаю Shift+Ctrl+Enter (Где matrica – присвоенное имя матрице А: «Вставка «Имя» «Присвоить» Указание имени и диапазона).

Ввожу вектор свободных членов B виде матрицы аналогично A.

Для того, чтобы найти решение системы линейных уравнений нужно A^-1*В

я выделяю столько же ячеек, сколько в данной матрице В, ввожу строку «=МУМНОЖ(b;obratnaia)» и нажимаю Shift+Ctrl+Enter (Где b – матрица В, obratnaia – матрица, обратная А)

Раздел 4. Построение графиков и диаграмм.

Создаю таблицу согласно заданию и заполняю незаполненные ячейки.

В А6 и В6 ввожу соответственно «1» и «Товар 1», растягиваю эти ячейки вниз до получения нужных значений. Столбцы «Количество» и «Цена» заполняю обычным способом. В ячейку F6 для подсчета суммы ввожу формулу «=C6*(D6+0,01*E6)» и копирую ее вниз. Множитель 0,01 необходим для того, чтобы перевести значения в копейках в дроби от рублей. В ячейку F18 ввожу формулу для подсчета автосуммы «=СУММ(F6:F17)» столбца «Сумма», выделенного голубым.

Для построения диаграммы я выделяю ячейки F6:F17 , выбираю «мастер диаграмм» и строю график зависимости суммы от количества. В качестве названия используется первая строка таблицы—«Накладная», в качестве значений Х задаю диапазон B6:B17—столбец «Количество».

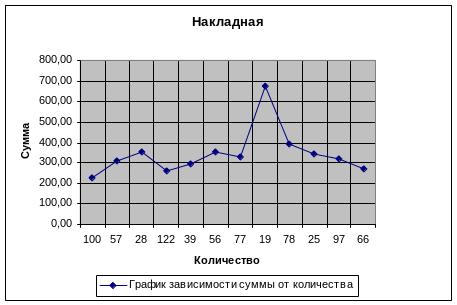
Раздел 5. Поиск решения.

Заполняю искомую таблицу:

Добавляю ещё несколько дополнительных строк и столбцов:

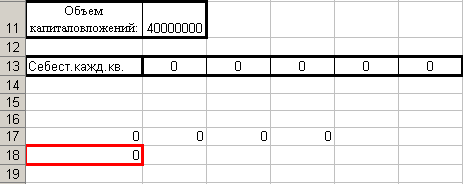
Строка «Себест.кажд.кв.» будет в дальнейшем изменяться, поэтому для начала заполним все ячейки нулями.

В ячейках A17:В17—расчет плановой себестоимости домов как суммы произведений себестоимости каждой квартиры на кол-во квартир каждого вида в разных домах: «=B3*B13+B4*B13+B5*B13+B6*B13+B7*B13», «=C3*C13+C4*C13+C5*C13+C6*C13+C7*C13», «=D3*D13+D4*D13+D5*D13+D6*D13+D7*D13», «=E3*F13+E4*F13+E5*F13+E6*F13+E7*F13»

В ячейке A18: «=B13*G3+C13*G4+D13*G5+E13*G6+F13*G7»--расчёт предположительных капиталовложений как суммы произведений себестоимости каждой квартиры на их плановое общее количество.

Затем СервисПоиск решения

В параметрах устанавливаю метки в окошке «Неотрицательные значения»Выполнить.

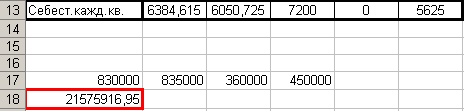
Значения в ячейках A17, B17, C17 и D17 совпали с соответствующими значениями в исходных данных ячеек B8, C8, D8 и E8. Что говорит о правильности найденного решения.

Вычислив разность между 40 млн. и значением в красной рамке я нахожу сумму, которая может быть потрачена на расширение сети коммунальных предприятий города--18424083,05.