Математический маятник.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

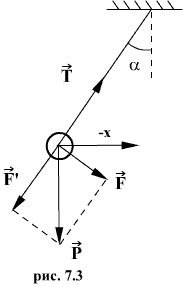
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: , и момент инерции:M = FL Момент инерции J в данном случае Угловое ускорение:

С учетом этих величин имеем: или

Его решение

,где и

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Физический маятник.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

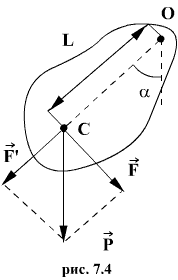
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

Решение этого уравнения

Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. или

.Из этого соотношения определяем

Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда Откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы называется резонансом.

Если затухание существует то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого , где - называют резонансной частотой. обозначает то значение циклической частоты ω вынуждающей силы, при котором .

Из последней формулы следует, что для консервативной системы , а для диссипативной системы несколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец при исчезает совсем.

Явление резонанса используется для усиления колебаний, например, электромагнитных. Однако при конструировании различных машин и сооружений необходимо учитывать даже самую небольшую периодическую силу с тем, чтобы предотвратить нежелательные последствия резонанса.