
- •Взаимодействие проводников о током
- •Закон Фарадея
- •Векторная форма
- •Дифференциальная форма
- •Интегральная форма
- •Материальные уравнения
- •Мощность в цепи переменного тока
- •Векторные и топографические диаграммы
- •Последовательная цепь переменного тока. Резонанс напряжений
- •Параллельная цепь переменного тока. Резонанс токов
- •Математический маятник.
- •Физический маятник.
Параллельная цепь переменного тока. Резонанс токов
В отличие от последовательных цепей переменного тока, где ток, протекающий по всем элементам цепи, одинаков, в параллельных цепях одинаковым будет напряжение, приложенное к параллельно включенным ветвям цепи. Рассмотрим параллельное включение емкости и ветви, состоящей из индуктивности и активного сопротивления
Обе ветви находятся под одним и тем же приложенным напряжением U Построим векторную диаграмму для этой цепи. В качестве основного вектора выберем вектор приложенного напряжения U
По
ветви с индуктивностью и активным
сопротивлением течет ток
![]() Длину
этого вектора найдем из соотношения
Длину
этого вектора найдем из соотношения
![]() и
отложим этот вектор по отношению к
вектору под углом
и
отложим этот вектор по отношению к
вектору под углом
![]() ,
который определяется по формуле
,
который определяется по формуле
![]()
Полученный
таким образом вектор тока
![]() разложим
на две составляющие: активную
разложим
на две составляющие: активную
![]() и
реактивную
и
реактивную
![]()
Величину
вектора тока
![]() текущего
по ветви с емкостью, находим из соотношения
текущего
по ветви с емкостью, находим из соотношения
![]()
и откладываем этот вектор под углом 90' против часовой стрелки относительно вектора приложенного напряжения .
Общий
ток в цепи
![]() равен
геометрической сумме токов
равен
геометрической сумме токов
![]() и
и
![]() или
геометрической сумме реактивного тока
или
геометрической сумме реактивного тока
![]() и
активного тока
и
активного тока
![]() Длина
вектора
Длина
вектора
![]() равна
равна
![]()
Сдвиг
по фазе между общим током
![]() и
приложенным напряжением
можно
определить из соотношения
и
приложенным напряжением
можно
определить из соотношения
![]()
Из
векторной диаграммы (рис. 4.21) видно, что
длина и положение вектора общего тока
зависят от соотношения между реактивными
токами
![]() и
и
![]() В
частности, при
>
,.
общий ток отстает по фазе от приложенного
напряжения, при
<
-
опережает его, а при
=
-
совпадает с ним по фазе. Последний случай
(
В
частности, при
>
,.
общий ток отстает по фазе от приложенного
напряжения, при
<
-
опережает его, а при
=
-
совпадает с ним по фазе. Последний случай
(![]() .)
называется резонансом токов.
При резонансе токов общий ток равен
активной составляющей тока в цепи, т.
е. происходящие в цепи процессы таковы,
как будто в ней содержится только
активное сопротивление (в этом случае
=
0 и
=1).
При резонансе общий ток в цепи принимает
минимальное значение и становится чисто
активным, тогда как реактивные токи в
ветвях не равны нулю и противоположны
по фазе.
.)
называется резонансом токов.
При резонансе токов общий ток равен
активной составляющей тока в цепи, т.
е. происходящие в цепи процессы таковы,
как будто в ней содержится только
активное сопротивление (в этом случае
=
0 и
=1).
При резонансе общий ток в цепи принимает
минимальное значение и становится чисто
активным, тогда как реактивные токи в
ветвях не равны нулю и противоположны
по фазе.
Гармоническими колебаниями называют такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса:
|
(7.1) |
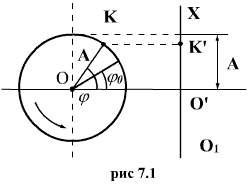
Для
иллюстрации физического смысла
![]() рассмотрим
окружность, и будем вращать радиус ОК
с угловой скоростью ω против часовой
(7.1) стрелки. Если в начальный момент
времени ОК лежал в горизонтальной
плоскости, то через время t он сместится
на угол
рассмотрим
окружность, и будем вращать радиус ОК
с угловой скоростью ω против часовой
(7.1) стрелки. Если в начальный момент
времени ОК лежал в горизонтальной
плоскости, то через время t он сместится
на угол
![]() .
Если начальный угол отличен от нуля и
равен φ0,
тогда угол поворота будет равен
.
Если начальный угол отличен от нуля и
равен φ0,
тогда угол поворота будет равен
![]() Проекция
Проекция
![]() на
ось ХО1
равна
на
ось ХО1
равна
![]() .
По мере вращения радиуса ОК изменяется
величина проекции, и точка
.
По мере вращения радиуса ОК изменяется
величина проекции, и точка
![]() будет
совершать колебания относительно точки
будет
совершать колебания относительно точки
![]() -
вверх, вниз и т.д. При этом максимальное
значение х равно А и называется амплитудой
колебаний; ω - круговая или циклическая
частота;
-
вверх, вниз и т.д. При этом максимальное
значение х равно А и называется амплитудой
колебаний; ω - круговая или циклическая
частота;
![]() -
фаза колебаний;
-
фаза колебаний;
![]() –
начальная фаза. За один оборот точки К
по окружности ее проекция совершит одно
полное колебание и вернется в исходную
точку.
–
начальная фаза. За один оборот точки К
по окружности ее проекция совершит одно
полное колебание и вернется в исходную
точку.
Кинетическая энергия:
|
|
Потенциальная энергия:
![]()
Учитывая
то, что
![]() т.е.
т.е.
![]() ,
последнее выражение можно записать в
виде:
,
последнее выражение можно записать в
виде:
|
|
Полная энергия колеблющегося тела равна сумме кинетической и потенциальной энергий
|
