§ 14. Окружность

Рассмотрим окружность с центром С(х₀, у₀) и радиусом R.

Уравнение (х – х₀)² + (у – у₀)² = R² представляет собой уравнение окружности радиуса R с центром в точке С(х₀, у₀). Это уравнение называют нормальным уравнением окружности.

Полагая х₀ = 0 и у₀ = 0, получим уравнение окружности с центром в начале координат: х² + у² = R².

Общее уравнение второго порядка для окружности имеет вид: Ах² + Ау² + Dx + Ey + F = 0.

Кривая второго порядка является окружностью тогда и только тогда, когда: 1) коэффициенты при квадратах текущих координат равны между собой и 2) отсутствует член, содержащий произведение текущих координат.

§ 15. Центральные кривые второго порядка

Рассмотрим уравнение кривой второго порядка:

А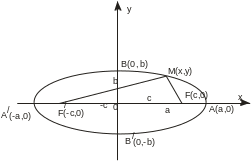 х² + Су² + Dx + Ey + F = 0. Кривая второго порядка называется эллипсом, если коэффициенты А и С имеют одинаковые знаки, т.е. А∙С > 0. Уравнение называется каноническим уравнением эллипса с полуосями а и b. Точки А(а, 0), В(0, b), А^/(-а, 0), B^/(0, -b) называются вершинами эллипса, а отрезки А^/A = 2a и B^/В = -2b – его осями. Из уравнения эллипса при а = b получаем уравнение окружность х² + у² = а².

В результате равномерной деформации окружности вдоль одного из ее диаметров получаем эллипс.

К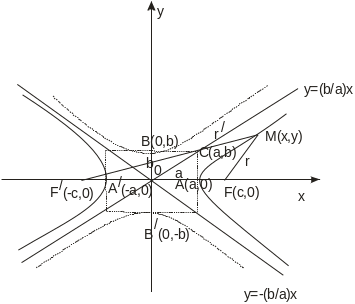 ривая второго порядка называется гиперболой, если коэффициенты А и С имеют противоположные знаки, т. е. А∙С < 0.

Каноническое уравнение гиперболы: ,

где а - действительная полуось, b = - мнимая полуось. Точки А(а, 0) и А^/(-а, 0) называются вершинами гиперболы.

Гипербола с полуосями а^/ и b^/ называется сопряженной к гиперболе , ее вершины будут B(0, b) и B^/(0, -b).

Ветви гиперболы сколь угодно близко подходят к прямых у = ± х, которые носят название асимптот гиперболы.

Пример. Определить вид и расположение кривой

х² + 2у² – 2х + 3у = 0.

Дополняя члены, содержащие х и у соответственно, до полных квадратов, будем иметь

(х – 1)² + 2(у + )² = 1 + . Отсюда получим

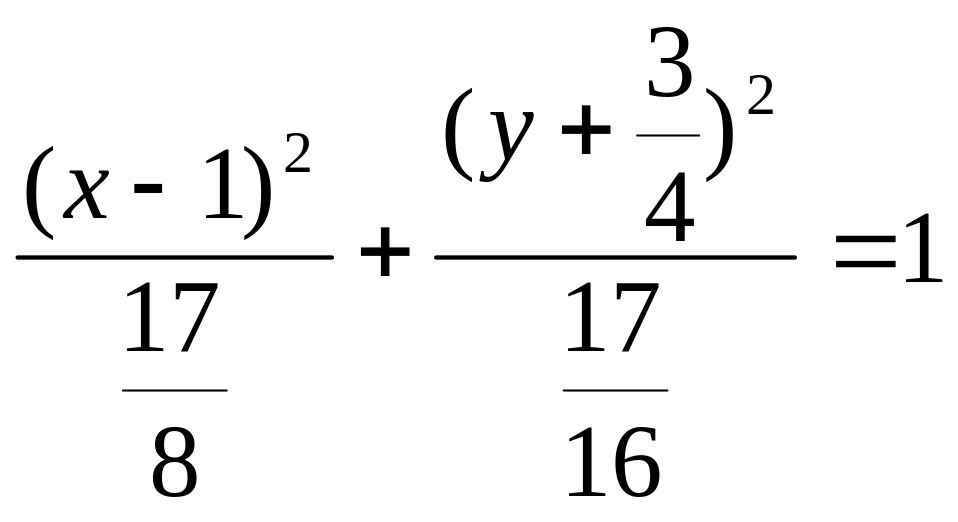. Следовательно, исходная кривая представляет собой эллипс с полуосями а = и b = , центр которого находится в точке О(1, - ).

§ 16. Фокальные свойства центральных кривых второго порядка

Точки F(c, 0) и F^/(-c, 0), где с = , называются фокусами, соответственно, эллипса, заданного каноническим уравнением (знак -), и гиперболы, заданной каноническим уравнением (знак +). Отношение ε = называется эксцентриситетом центральной кривой второго порядка.

Для эллипса 0 ≤ ε < 1, для гиперболы 1 < ε < +∞. Для окружности ε = 0.

Для любой точки эллипса сумма ее фокальных радиусов есть величина постоянная (характеристическое свойство эллипса). Это свойство часто принимают для определения эллипса.

Для любой точки гиперболы модуль разности ее фокальных радиусов есть величина постоянная (характеристическое свойство гиперболы).

§ 17. Нецентрические кривые второго порядка

Кривая второго порядка называется нецентрической, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии.

Рассмотрим кривую второго порядка вида: Ах² + Су² + Dx + Ey + F = 0, где А∙С = 0 и А² + С² ≠ 0. Для определенности будем считать, что А = 0, С ≠ 0. Кроме того, предположим, что D ≠ 0.

У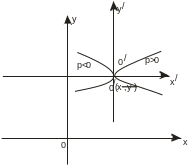 равнение (у – у₀)² = 2р(х – х₀) описывает кривую, которая называется параболой. Точка О^/(х₀, у₀) - вершина параболы, а число р называется параметром параболы. Прямая у = у₀ является осью симметрии параболы (ось параболы). Центра симметрии парабола не имеет.

Если вершина параболы находится в начале координат, а ее осью является ось Ох, то получаем к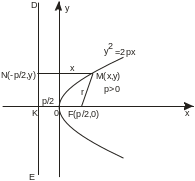 аноническое уравнение параболы вида: у² = 2рх. Причем параметр р здесь обычно считается положительным. Если поменять местами оси Ох и Оу, то каноническое уравнение параболы примет вид: х² = 2ру. Это уравнение параболы с вертикальной осью.

Рассмотрим параболу у² = 2рх (p > 0). Точка F(p/2,0) называется фокусом параболы, а прямая х = -р/2 называется директрисой параболы.

Парабола представляет множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это есть характеристическое свойство параболы.

Пример 1. Определить координаты фокуса и уравнение директрисы параболы у = х².

Сравнивая это уравнение с уравнением х² = 2ру, получим 2р = 1, отсюда р = ½. Следовательно, фокус параболы имеет координаты (0, ¼), а уравнение директрисы есть у = -1/4.

Пример 2. Привести уравнение у = х² – 4х + 3 к каноническому виду и построить соответствующую параболу.

Перенося свободный член в левую часть уравнения и дополняя правую часть до полного квадрата, будем иметь у – 3 +4 = х² -4х + 4 или у + 1 = (х – 2)².

Полагая х – 2 = х^/, у + 1 = у^/, получим у^/ = x^/2. Таким образом, заданное уравнение есть уравнение параболы с вершиной в точке 0^/(2, -1) и осью симметрии О^/у^/, параллельной оси Оу.