2

Аналитическая геометрия на плоскости

Задачей аналитической геометрии является исследование методами математического анализа формы, расположения и свойств линий.

§ 1. Расстояние между двумя точками на плоскости

.

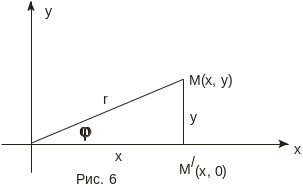Расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки.

Пусть даны две точки А(х₁, у₁) и В(х₂, у₂), тогда

d = .

Расстояние между двумя точками плоскости равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

Последняя формула дает также длину отрезка АВ.

d_x = x₂ – х₁, d_y = у₂ – y₁ называются проекциями отрезка АВ на оси координат Оху. Отсюда получаем

§ 2. Деление отрезка в данном отношении

Пусть отрезок АВ, соединяющий точки А(х₁, y₁) и В (х₂, y₂), разделен точкой С на два отрезка АС и СВ, причем отношение АС к СВ равно l (l > 0), т. е. .

К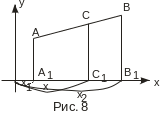 оординаты точки С(х, у), делящей отрезок АВ в отношении l(считая от А к В), определяются по формулам:

х = ; у = .

Если точка С делит отрезок АВ пополам, т.е. АС = СВ и, следовательно, l = . Тогда получим

х = ; у = .

Координаты середины отрезка равны полусуммам соответствующих координат его концов.

§ 3. Площадь треугольника

Площадь S треугольника ABC с вершинами A(x₁, у₁), В(х₂, у₂), С(х₃, у₃) определяется по формуле:

S = |((х₂ – х₁)(у₃ – у₁) – (x₃ – x₁)(y₂ – y₁))|.

Используя понятие определителя второго порядка

= ad - bc

формулу для площади треугольника можно записать в более удобной форме:

S = ± .

Формула для площади треугольника упрощается, если точка А(х_1, у₁) находится в начале координат. А именно, полагая х₁ = 0, у₁ = 0, получим

S = |(x₂y₃ – x₃y₂)|.

УПРАЖНЕНИЯ

Пример. Вычислить координаты точки С(х, у), делящей отрезок АВ между точками А(-5, -3) и В(4, -6) в отношении АС/СВ = 3/2.

Решение. В этом случае l = 3/2 и, следовательно,

x = , y = .

Пример. Вспаханное поле имеет форму треугольника с вершинами А(-2, -1), В(3, 5) и С(-1, 4) (размеры даны в километрах). Определить площадь S этого поля.

Решение:

S = ± ± = 9.5 км²,

1. На оси Ох найти точку, расстояние от которой до точки А (3, 4) равно 5.

2. Отрезок АВ, где А(2, 5) и В(4, 8), делится точкой С в отношении 2:3. Найти координаты точки С.

3. Точка С(2, 3) делит отрезок АВ в отношении 1:2. Найти координаты точки В, если известно, что точка А имеет координаты х = 1, у = 2.

4. Вершины треугольника суть А(-2, 0), В(6, 6) и С(1, -4). Найти длину биссектрисы, проведенной из вершины А.

5. В точках А(-2, 1) и В(7, 4) помещены соответственно m₁ = 10 г и m₂ = 20 г. Определить координаты центра масс этой системы.

6. Найти координаты центра масс N треугольника ABC с вершинами: А(-2, 1), В(2, -1), С(4, 3). (Центр масс треугольника совпадает с точкой пересечения его медиан, которая, как известно, делит каждую из медиан в отношении 2:1, считая от вершины).

7. Отрезок между точками А(x₀, у₀) и В(х, у) разделен на n равных частей. Определить координаты x_i, y_i (i = 1, 2, ..., n - 1) точек деления.

8. Вычислить площадь треугольника с вершинами А(-2, -2), В(-1,3) и С(3,-1).

9. Показать, что точки А(-7, -3), В(-1, 1) и С(2, 3) лежат на одной прямой.

10. Площадь треугольника ABC с вершинами А(-2, 1); В(2, 2) и С (4, y) равна 15. Определить ординату вершины С.