30. Плотность распределения

            Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток.  По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

             Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

            Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

            Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

            После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

             Определение.  Случайная величина Х называется непрерывной, если ее функция распределенияF(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.

             Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

             Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.

             Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.

№31. Равномерное распределение НСВ: ф-я распр-я, плотность расп-я, график, мат ожидание, дисперсия

Понятие НСВ,  функция ее распределения

Случайной непрерывной  величиной является величина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим воз­можных значений случайной величины.  

Случайной непрерывной  величиной является величина, функция распределения F(x) которой, непрерывна на всей числовой оси.

Функция распределения HСВ F(x) есть кусочно-дифференцируемая функция с не­прерывной производной.

Вероятность того, что случайная величина примет значение, заключенное в некотором интервале (а, b), равна приращению функции распределения на этом ин­тервале;P(a ≤ X ≤b) = F (b) - F (а).

При рассмотрении функции распределения, числовой промежуток записывается так же в виде [x₁; x₂], тогда вероятность того, что случайная величина примет значение, заключенное в этом интервале равна:

p(x₁≤ x ≤ x₂) = F (x₂) - F (x₁).-  что более понятно и привычно.

Вероятность того, что случайная непрерывная величина X примет одно определенное значение, равна нулю.

 Понятие плотности распределения, функция плотности НСВ

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (х) - первую производную от функции распределения F (х): f (х)= F'(х)

Из этого определения следует, что функция распре­деления F(х) является первообразной для плотности распре­деления f (х):  F(х)= f (х).

Функцию f (х) можно называть дифференциальной функцией

Таким образом, зная интегральную функцию (функцию распределения) можно найти дифференциальную функцию(функцию плотности) и наоборот по формулам:f (х)= F'(х)                               F(х)= f (х).

Математическим ожиданием  непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

            Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

            При этом, конечно, предполагается, что несобственный интеграл сходится. Свойства математического ожидания НСВ аналогичны свойствам математического ожидания ДСВ.

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

            По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

№32    Нормальное расп-е

Это такое расп-е случ.велечины Х, плотность Р которого опис. Формулой f(x)=(1/(x)*2)*exp(-(x-M(x)² )/(2²(x), где (х)- сред.квадрат.отклонение, М(х)-матем.ожидание

№33 Нормальное расп-е: 1)вероятность попадания в заданный интервал, вероятность заданого отклонения

1)Если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее заданному интервалу, вычисляется по формуле . Подставив в формулу значение плотности распределения из для нормального распределения N(a, s) и сделав ряд преобразований, вероятность того, что Х примет значение, принадлежащее заданному интервалу [x₁, x₂], будет равна:

Где а-мат.ожидание

2)

P (|X–a| ≤ e) = 2Ф(/s) = 2Ф(t), где

№34 Показательное расп-е НСВ: график, ф-я расп-я, плотность расп-я, матем ожидание, дисперсия

№35 Показательное расп-е: ф-я надежности, показательный закон надежности, характеристичесткое свойство этого закона

Функция надежности

Будем называть элементом некоторое устройство независимо от того, "простое" оно или "сложное".

Пусть элемент начинает работать в момент времени t₀=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину - длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t то, следовательно, за время длитель­ностью t наступит отказ.

Таким образом, функция распределения F (t)=P(T<t) определяет вероятность отказа за время длитель­ностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность про­тивоположного события Т > t, равна

Функцией надежности R (t) называют функцию, определяющую надежность работы элемента за время длительностью t:

Показательный закон надежности

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого

Следовательно, функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид

Показательным законом надежности называют функ­цию надежности, определяемую равенством

где  интенсивность отказов

Как следует из определения функции надежности, эта формула позволяет найти вероятность без­отказной работы элемента на интервале времени длитель­ностью t_t если время безотказной работы имеет, показа­тельное распределение.

Характеристическое свойство показательного закона надежности.

Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обла­дает следующим важным свойством: "Вероятность безот­казной работы элемента на интервале времени длитель­ностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивно­сти отказов )".

Итак, в случае показательного закона надежности безотказная работа элемента "в прошлом" не сказывается на величине вероятности его безотказной работы "в бли­жайшем будущем".

Замечание. Можно доказать, что рассматриваемым свойством обладает только показательное распределение. Поэтому если на практике изучаемая случайная величина этим свойством обладает, то она распределена по показательному закону. Например, при допу­щении, что метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попадали или не попадали метеориты в корабль до начала рассматриваемого интервала времени. Следовательно, слу­чайные моменты времени попадания метеоритов в космический корабль распределены по показательному закону.

№36 Ф-я одного случ аргумента, матем ожидание

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y  называют функцией случайного аргу-мента Х:               Y = φ(X).                                                                                                                 Выясним, как найти закон распределения функции по известному закону распределения аргумента.

1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны.

2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются.

3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х), то плотность распределения g(y) случайно функции Y равна: 

                 Математическое ожидание функции одного случайного аргумента.

Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.

1)      Если Х – дискретная случайная величина, то

                                                                                  

Пример 3. Найдем  M(Y) для примера 1:  M(Y) = 47·0,1 + 69·0,2 + 95·0,3 + 125·0,4 = 97.

2)      Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то

                                                                                                     

Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):

                                                                                               

В частности, если все значения Х принадлежат промежутку (а, b), то                              

№37 Ф-я двух случ аргументов, закон расп-я

Если каждой паре возможных значений случайных величин Х и Y соответ-ствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y :  Z = φ(X, Y).

Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.

1) Если  X и Y – дискретные независимые случайные величины, то для определения закона распределения   Z = Х + Y нужно найти все возможные значения Z и соответствующие им вероятности.

3)      Если  X и Y – непрерывные независимые случайные величины, то, если плотность вероятно-сти хотя бы одного из аргументов задана на (-∞, ∞) одной формулой, то плотность суммы g(z) можно найти по формулам

                                                             

где f₁(x), f₂(y) – плотности распределения слагаемых. Если возможные значения аргументов неотрицательны, то

                                                             

Замечание. Плотность распределения суммы двух независимых случайных величин называют композицией.

№38 Закон больших чисел: неравенство Чебышева

Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа не меньше чем :

p( | X — M(X)| < ε ) ≥ D(X) / ε².

Доказательство. Пусть Х задается рядом распределения

Х х1 х2 … хп р р1 р2 … рп	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X — M(X)| < ε и |X — M(X)| ≥ ε противоположны, то р ( |X — M(X)| < ε ) + + р ( |X — M(X)| ≥ ε ) = 1, следовательно, р ( |X — M(X)| < ε ) = 1 - р ( |X — M(X)| ≥ ε ). Найдем р ( |X — M(X)| ≥ ε ).

D(X) = (x₁ — M(X))²p₁ + (x₂ — M(X))²p₂ + … + (x_n — M(X))²p_n . Исключим из этой суммы те слагаемые, для которых |X — M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

D(X) ≥ (x_k+1 — M(X))²p_k+1 + (x_k+2 — M(X))²p_k+2 + … + (x_n — M(X))²p_n ≥ ε² (p_k+1 + p_k+2 + … + p_n).

Отметим, что p_k+1 + p_k+2 + … + p_n есть вероятность того, что |X — M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X — M(X)| ≥ ε), или р (|X — M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X — M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.

№39 Теоремы Чебышева и Бернули

Теоремы Чебышева и Бернулли.

Рассмотрим последовательность случайных величин   (2).

Введем среднее арифметическое:

Запишем математическое ожидание:

 Обозначим

Def: говорят, что для последовательности выполняется закон больших чисел, если для любого справедливо равенство:

О равенстве (3) также говорят, что среднее арифметическое случайных величин в вероятностном смысле (по вероятности) сходится к среднему арифметическому их математических ожиданий.

Если последовательность случайных величин (2) удовлетворяет закону больших чисел, то, как видно из равенства (3), среднее арифметическое ведет себя фактически как величина неслучайная, поскольку ее значение в вероятностном смысле как угодно мало отличается от числа (среднего арифметического математического ожидания случайной величины ).

Теорема Чебышева: пусть случайные величины последовательности (2) таковы, что:

1) Они попарно независимы.

2) Имеют конечное математическое ожидание.

3) Имеют равномерно ограниченные дисперсии

Тогда к последовательности применим закон больших чисел.

Доказательство.

Оценим дисперсию:

Применим неравенство (1):

Левую часть выразим через вероятность противоположного события:

Умножим обе части на (-1):

С другой стороны:

На основании двух предыдущих формул получаем формулу (3)

 

 

Теорема Бернулли: относительная частота события “А” в вероятностном смысле сходится к вероятности этого события:

      (4)

Доказательство.

С каждым испытанием свяжем случайную величину .

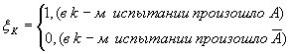
Тогда число наступлений события “А” в “n” независимых испытаний будет равно:

Покажем, что к этой последовательности применим закон больших чисел (равенство 3). Проверим выполнение условий теоремы Чебышева:

1) – попарно независимы.

2)

3)

Таким образом в силу теоремы Чебышева к последовательности случайных величин { } применим закон больших чисел, выражаемый равенством (3). В данном случае среднее арифметическое:   – относительная частота.

В силу (3) получаем равенство (4).

№40 Оценка отклонения распределения НСВ от нормального коэффициента ассиметрии и эксцесса

Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическиможиданием, например, нормальным, все нечетные моменты, в том числе итретий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю. Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной - коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса большенуля, то распределение имеет более острую вершину, чем распределениеГаусса, если меньше нуля, то более плоскую. Для расчета коэффициентов асимметрии и эксцесса в MathCAD имеютсядве встроенные функции. - kurt (x) - коэффициент эксцесса (kurtosis) выборки случайных данных х; - skew(x) - коэффициент асимметрии (skewness) выборки случайных данных X .

№41 Распределение «хи-квадрат»

Пусть х₁,х₂,…,х_n-независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1,тогда закон расп-я суммы кварт.величин(Х-квадрат) х²=х₁ ²+х₂²+…+х_n² назв. Законом Х-квадрат с nстепенями свободы. Плотность расп-я этого закона опред:

0, при х<0

f(x) (e^-x/2*x^n/2-1)/2^n/2+Г’(n/2)^x ≥0

№42 распределение Стьюдента

Пусть х₀,х₁,…,х_n-независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1, тогда величина опред по ф-ле:Т=( х₀/^m_n=1*x²/n) назв. Величиной имеющей расп-е Стьюдента с n-степенями свободы

Плотность имеет вид f(x)= b_n(1+ x²/2)^-((n+1)/n)

b_n=Г((n+1)/2)/Гn/2*n

№43 Распределение Фишера-Снедекора

Пусть х₁,х₂,…,х_n ,у₁,у₂,…,у_n независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1, тогда случ величина ,заданная ф-лой F_nm=((x_i ²/n)/ y_j ²/m) назв. Случ величиной, имеющей расп-е Фишера-Снедекора с n и m степенями свободы, плотность расп-я имеет вид

F(x)= 0,при x0

C₀ *(x^(n-2)/2/(n+n x^(+2)/2),для х>0

C₀=Г(((n+m)/2)*n^n/2 *m ^m/2 ))Г ^n/2Г ^m/2

№44 Система двух случайных величин. Закон расп-я.Ф-я расп-я. Свойства функции расп-я

Законом расп-я назв перечень возможных значений двумерн величины , т.е А(x_i,у_i) и их соотв. Вероятностей Р(x_i,у_i). Обычно закон задают таблицей с двойным ходом.1строка-все возможн.значения. составляющие х.1 столбец- все возможн.значения. составляющие у клетки на их пересечении (x_i,у_i) заполняют соответств. Вероятность , причем кол-вл знач-й х,у могут быть различными, т.к событие х=у_i и у=у_i образуют полную группу , то сумма вероятностей помещенных во всех клетках =1.

Ф-я расп-я:

Пусть х,у пара действительных чисел, вероятность события состоит в том, что составляющая х примет знач-е меньше х; составляющая у примет знач-е меньше у. X<x; Y<y. обозначение Р(X<x; Y<y)=F(x;y) – ф-я расп-я

Свойства функции расп-я

1.Значения ф-и расп-я удовлетв. Неравенству 0< F(x;y)<1

2. Ф-я F(x;y) явл. Неубывающей ф-ей.

3. Имеют место след соотношения:1)F(-∞; y)=0 2) F(x;-∞)=0 3) F(-∞;-∞)=0 4) F(+∞;+∞)=1

4. При у=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей х. При х=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей у

№45 Система двух случайных величин: плотность совместного расп-я вероятностей, нахождение ф-и расп-я по плотности расп-я, свойства двумерной плотности расп-я

Плотность совм.расп-я вероятностей назв частную производную второго порядка, смешанная по переменным х, у

нахождение ф-и расп-я по плотности расп-я

F(x,y)=sinx*siny

0x/2; 0y/2

Решение:

F_х(x,y)=cosx*siny ;F_xy= cosx cosy. Зная плотность расп-я можно найти ф-ю расп-я F(x,y)=-_∞^∞ -_∞^∞f(x,y) dx dy

свойства двумерной плотности расп-я:

1.плотность вероятности не отрицательна f(x,y)≥0

2. -_∞^∞ -_∞^∞f(x,y) dx dy=1

3. можно найти плотность расп-я для каждой составляющей

46.       Определение. Плотностью совместного распределения  вероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.

Условные законы распределения составляющих системы дискретных случайных величин.

Рассмотрим дискретную двумерную случайную величину 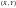, пусть возможные значения составляющих таковы:

Предположим, что в результате испытания случайная величина Y приняла значение , тогда X может принять одно из своих возможных значений. Обозначим условную вероятность того, что X примет значение через

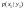
Условным распределением случайной величины X при условии, что Y приняла значение 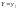называют совокупность условных вероятностей

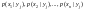
Зная закон распределения двумерной дискретной случайной величины можно вычислить условные законы распределения составляющих:

Условные законы распределения составляющих системы непрерывных случайных величин

Условной дифференциальной функцией составляющей X при условии, что , называют отношение дифференциальной функции системы к дифференциальной функции составляющей Y.

47. Условное математическое ожидание

Условным математическим ожиданием случайной величины Y при 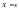называют сумму произведений возможных значений Y на их условные вероятности.

Для непрерывных величин:

48. Зависимые и независимые случайные величины

Теорема. Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы интегральная функция системы была равна произведению интегральных функций случайных величин X и Y.

Следствие. Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы дифференциальная функция системы была равна произведению дифференциальных функций случайных величин X и Y.

КОРРЕЛЯЦИОННЫЙ МОМЕНТ  Корреляционным моментом двух случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: _xy = M{[X - M(X)][Y - M(Y)]}. Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Если корреляционный момент не равен нулю, то X и Y - зависимые случайные величины. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, корреляционный момент зависит от единиц измеренияслучайных величин. Безразмерной числовой характеристикой связи двух случайных величин является коэффициент корреляции.

коэффициент корреляции. Он рассчитывается следующим образом:

Есть массив из n точек {x_1,i, _x2,i}

Рассчитываются средние значения для каждого параметра: 

И коэффициент корреляции: 

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x₁ и x₂: r равен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы: