Алгоритм відшукання оптимального плану.
Після знаходження опорного плану обчислюються значення визначників:
,
значення яких заносяться в додатковий рядок таблиці.
В стовпчику вільних членів в цьому рядку записуємо значення функціоналу, рівне відношенню F1 i F2
В результаті приходимо до таблиці (Табл.3):
Табл.3
|
-y 1 -y 2 -x s -x n |
1 |
х1= х2= ym= |
b 11 b 12 b 1s b 1n b 21 b 22 b 2s b 2n b m1 b m2 b ms b mn |
b 1 b 2 b m |
F1= F2= |
p 1 p 2 p s p n q 1 q 2 q s q rn |
0 0 |
dj= |
d 1 d 2 d s d n |
|
При розв’язуванні задачі на максимум функціоналу за розв’язуючий стовпчик вибираємо той, в якому dj < 0. Коли таких стовпчиків декілька, то за розв’язуючий стовпчик краще брати той, в якому dj найбільший по абсолютній величині.
Розв’язуючи елемент в стовпчику шукається по найменшому симплексному відношенню.
Із знайденим brs робимо один крок МЖВ при цьому коефіціенти стрічок F1 і F2 перетворюються за загальним правилом, а останній рядок не перетворюється і не записується.
Далі для кожного стовпчика обчислюємо визначники dj, а для плану - значення функціоналу F(k+1). Якщо серед dj є хоча б один від’ємний, то робимо новий крок МЖВ і т. д.
Оптимальний розв’язок буде досягнуто, коли після чергового кроку всі визначники dj стануть невід’ємними.
При розв’язуванні задачі на мінімум, за розв’язуючий приймається стовпчик з dj > 0. Критерієм оптимальності служить недодатність dj.
ПРИКЛАД.
Знайти максимум та мінімум функціоналу:
При виконанні обмежень:
РОЗВ’ЯЗАННЯ.
Складаємо початкову жорданову таблицю, заповнюючи коефіцієнтами функціоналу для чисельника та знаменника окремо два рядки F1 F2 (Табл.4).
Табл.4
1 |
-x 1 -х 2 -x 3 |
|
y1= y2= y3= |
-3 6 1 -1 7 2 -2 4 -1 |
2 12 -1 |
F1= F2= |
1 2 -1 3 1 5 |
0 0 |
Так як b3 = -1 < 0, то план х1 = х2 = х3 = 0 не є опорним.
Знайдемо опорний план. Відшукавши такий план, додаємо до таблиці ще один рядок, в який записуємо значення dj і функціоналу F (Табл.5) .
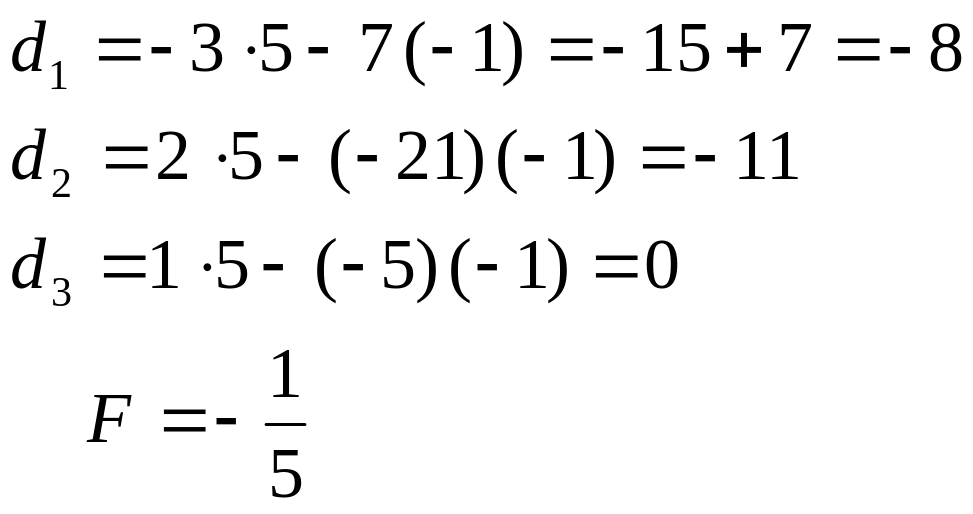
Табл.5
2 |
-x 1 -х 2 -y 3 |
|
y1= y2= x3= |
-5 10 1 -5 15 2 2 -4 -1 |
1 10 1 |
F1= F2= |
-3 2 1 7 -21 -5 |
-1 5 |
dj |
-8 -11 0 |
-1/5 |
Оскільки всі визначники dj недодатні, робимо висновок, що функціонал досягає мінімуму у вершині
x1
= 0, x2
= 0, x3
= 1
Для знаходження максимуму вибираємо за розв’язуючий другий стовпчик. Розв’язуючий елемент brs = 10. З цим елементом робимо крок МЖВ, перетворюючи всю таблицю, крім останнього рядка dj. В результаті отримаємо таблицю виду (Табл.6).
Табл.6
3 |
-x 2 -y 1 -y 3 |
|
x2= y2= x3= |
-1/2 1/10 1/10 5/2 -3/2 ½ 0 2/5 -3/5 |
1/10 17/2 7/5 |
F1= F2= |
-2 -1/5 4/5 -7/2 21/10 -29/10 |
28/5 7/5 |
dj= |
-92/5 11/10 11/5 |
-12/71 |
Елемент
від’ємний – це означає, що максимум ще
не досягнуто.
В першому стовпчику
вибираємо за розв’язуючий елемент
з ним робимо наступний крок МЖВ і
отримаємо нову таблицю (Табл.7).
Табл.7
4 |
-y 2 -y 1 -y 3 |
|
x1= x2= x3= |
1/5 -1/5 1/5 2/5 -3/5 1/5 0 2/5 -3/5 |
9/5 17/5 7/5 |
F1= F2= |
4/5 -7/5 6/5 7/5 0 -11/5 |
28/5 19 |
dj= |
184/25 -133/5 878/25 |
28/15 |
Обчисливши в новій
таблиці всі
знову знаходимо один від’ємний, а тому
робимо ще один крок МЖВ з елементом
.
В результаті отримали таблицю (Табл.8).
Табл.8
5 |
-y 2 -y 1 -x 3 |
|
x1= x2= y3= |
1/5 1/2 -1/10 2/5 3/2 -7/10 0 5/2 -3/2 |
5/2 11/2 7/2 |
F1= F2= |
4/5 -7/2 -9/10 7/5 0 -11/5 |
21/2 19 |
dj= |
|
|
В Табл.8 всі
визначники dj
невід’ємні. Це свідчить про те, що при
значеннях невідомих
функціонал досягає максимального
значення
.
Задача розв’язана.