Задача дробово-лінійного програмування.

1. Приклад економічної задачі та її математичне формулювання.

Нехай виробництво випускає однорідний продукт і володіє технологічними способами (технологіями).

При роботі за цими технологіями за одиницю часу підприємство отримує продукту відповідно q₁, q₂,…q_n,. а виробничі витрати за одиницю часу складають p₁, p₂,…p_n, одиниць.

Якщо план, по якому підприємство буде працювати за відповідними технологіями складає x₁, x₂,…x_n – одиниць часу, то загальний випуск продукції буде рівний:

, (1.1)

а загальні витрати складають:

(1.2)

Відношення загальних витрат до загального об’єму продукту, що випускається визначає економічний показник, що називається собівартістю продукції.

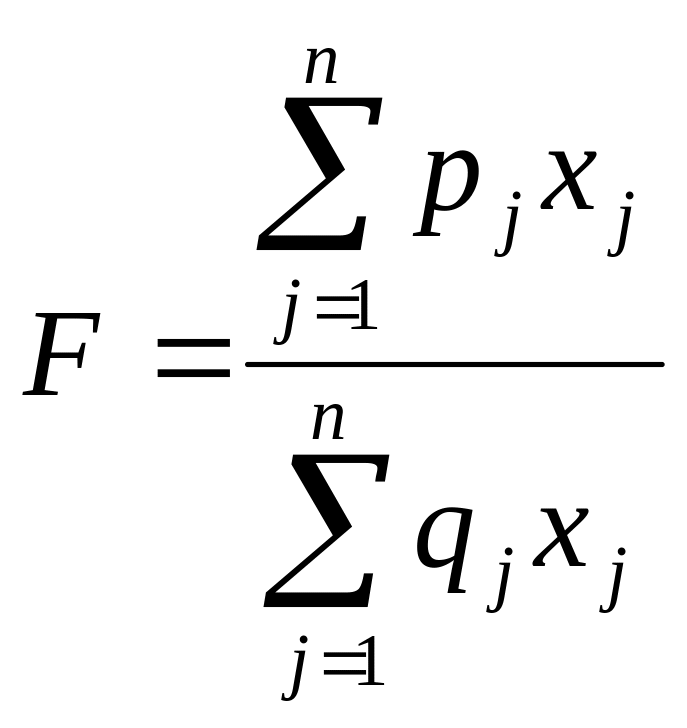(1.3)

Економічний зміст задачі: скласти такий план роботи підприємства (знайти час роботи по кожній технології), при якому собівартість продукції була б мінімальною і одночасно виконувались би деякі умови (обмеження).

При плануванні виробництва намагаються знизити цей показник, щоб випускати продукцію з найменшими витратами.

Функція виду

називається дробово-лінійною.

Собівартість є не єдиним економічним показником, що має дробово-лінійну структуру (наприклад, рентабельність).

Загальна задача Д-ЛП полягає у визначенні максимального (мінімального) значення функціоналу:

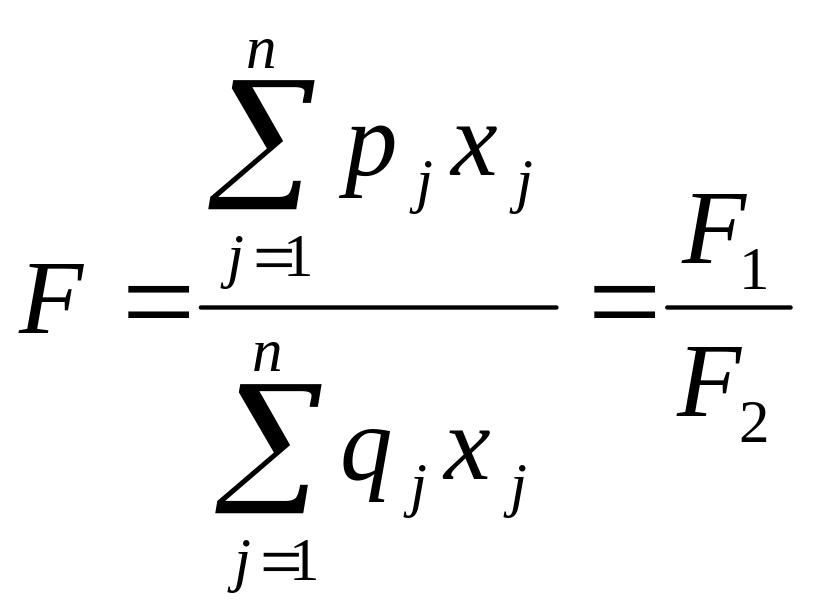
 max(min) (1.4)

за умов:

(1.5)

, (1.6)

де p_j, q_j, a_i, - деякі постійні числа, а

(1.7)

(коли , то знак можна віднести до чисельника).

2. Геометричний зміст і графічний спосіб розв’язання задачі дробово-лінійного програмування.

Розглянемо на площині Ox₁x₂ цільову функцію:

(2.1)

звідки виразимо x₂:

ввівши позначення: , отримаємо: x₂=k x₁.

x₂=k x₁ - пряма, яка проходить через початок координат.

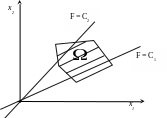
Рис.1

Визначимо, як буде поводити себе кутовий коефцієнт k при монотонному зростанні функції . Для цього візьмемо похідну від k по .

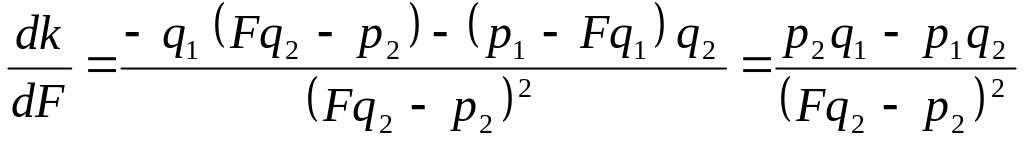
(Fq₂-P₂)² , а чисельник не залежить від F.

Отже, похідна має постійний знак і при зміні F кутовий коефіцієнт буде або тільки зростати, або тільки спадати і пряма буде повертатися в одну сторону. При повороті прямої в одному напрямку функціонал F також буде або зростати або спадати. Встановивши напрямок повороту для зростання F, знаходимо необхідну вершину многогранника поворотом прямої навколо початку координат.

При цьому можливі такі випадки:

1. М 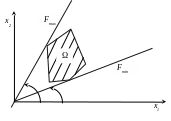ногокутник  обмежений (Рис.2), максимум і мінімум є (стрілки на малюнку показують напрямок повороту прямої для збільшення F).

Рис.2

2. О 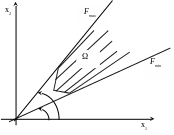бласть необмежена, але максимум і мінімум є (Рис.3).

Рис.3

3. Область необмежена, і один із екстремумів не досягається (Рис.4).

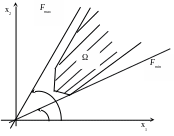
Рис.4

4. О 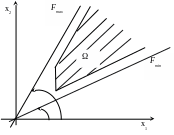бласть необмежена, обидва екстремуми асимптотичні (Рис 5).

Рис.5

ПРИКЛАД.

Знайти максимум і мінімум функціоналу графічним методом.

при обмеженнях

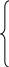
РОЗВ’ЯЗАННЯ.

Б удуємо область допустимих розв’язків (Рис.6). Очевидно, що екстремальними будуть точки А і В.

Рис 6.

Визначимо де буде max, а де min. Виразимо з із цільової функції x₂ : ,

Так як при будь-якому F функція спадна, зі збільшенням F кутовий коефіцієнт k зменшується. Це відповідає повороту за годинниковою стрілкою. Отже, в тоці А(2;3) значення F буде найменшим, а у вершині В(4;1) – найбільшим. Обчислимо значення функціоналу в цих точках.

Оскільки F_A < F_B, то і .