Размерные цепи и методы их решения при сборке

При соединении деталей в процессе сборки необходимо обеспечить их взаимное расположение в пределах заданной точ­ности. Сопряжение подвижных поверхностей должно обеспе­чить заданный зазор, а неподвижных — необходимый натяг. Заданная точность соединения деталей при сборке без допол­нительной пригонки будет обеспечена при изготовлении деталей станков в пределах отклонений, указанных в чертежах. Вслед­ствие этого детали в собранных узлах должны быть взаимо­связаны.

Взаимосвязь и взаимозависимость размеров деталей в со­бранных узлах или механизмах называют размерными связями деталей. Размерные связи деталей образуют сборочные размер­ные цепи.

Размерной цепью называют группу сопряженных линейных или угловых размеров, образующих замкнутый контур, отклонения в которых влияют на точность одного из размеров кон­тура. Размерная цепь состоит из отдельных звеньев. Звеньями размерной цепи называют размеры детали или узла, величины перекосов осей, поверхностей и так далее, образующие размер­ную цепь. Например, размеры А₁, А₂, А_ (рис. 145, а и б), раз­меры А₁, А₂, А₃, А₄, А₅, А_ (рис. 145, в) являются звеньями раз­мерной цепи.

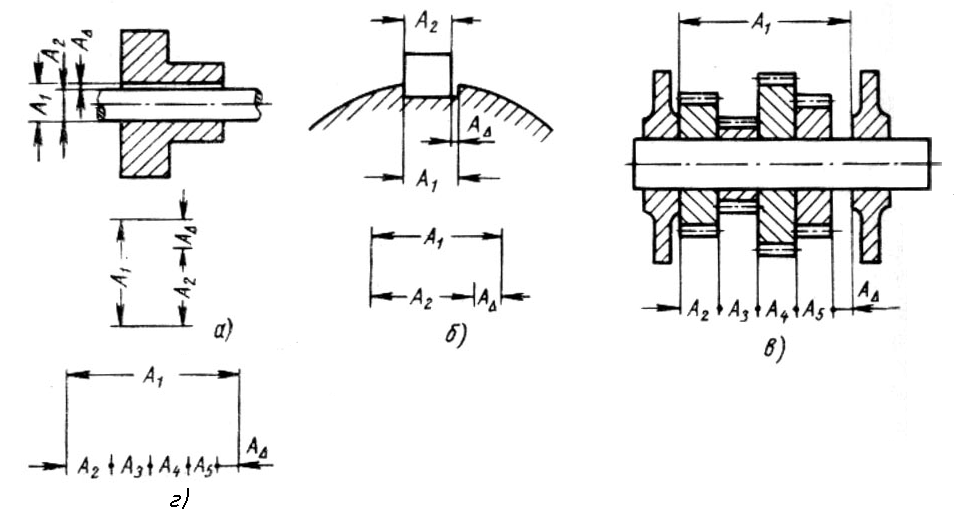
Рис. 145. Примеры соединения деталей и схемы их размерных цепей:

а — муфта с валом; б — шпонка с валом; в — набор зубчатых колес с валом

Все звенья размерной цепи подразделяют на исходное, или замыкающее звено и составляющие звенья.

Исходным, или замыкающим, называют звено, по номиналь­ному размеру и допуску которого рассчитывают номинальные размеры и допуски всех остальных звеньев размерной цепи.

Уравнение размерной цепи. Расчет размерной цепи сводится к определению номинальных размеров и допусков для отдель­ных звеньев. Он основан на том, что величина замыкающего звена размерной цепи равна алгебраической сумме величин всех остальных ее звеньев. Если обозначить номинальные размеры звеньев размерной цепи буквами А₁, А₂, А₃, … А_n, то уравнение номинальных размеров размерной цепи будет иметь вид

А_ =(А₁ + А₂ + … + А_n) – (А_n+1 + А_n+2 + … + А_m-1)

или ,

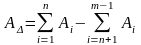где А_ — номинальная величина замыкающего звена;

А₁, А₂, …, А_n — номинальные размеры звеньев размерной цепи;

n — число звеньев увеличивающей ветви;

m — число звеньев в размерной цепи.

Величина ошибки замыкающего звена равна сумме ошибок всех остальных звеньев размерной цепи. Если на каждый номи­нальный размер размерной цепи установить допуск, то возмож­ная ошибка размеров замыкающего звена цепи равна сумме допусков всех звеньев, составляющих данную размерную цепь

А_ =А₁ + А₂ + … + А_m-1 или ,

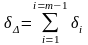где _ — допуск замыкающего звена;

_i —допуск остальных звеньев цепи;

m — число всех звеньев в цепи.

i—m— 1

Выражение называется основным уравнением размерной цепи.

Зная допуски отдельных звеньев цепи, можно определить допуск замыкающего звена. Например, для размерной цепи (рис. 146) допуск замыкающего звена

А_ =А₁ + А₂ + А₃ + А₄ + А₅ = 0,25 + 0,15 + 0,15 + 0,1 + 0,2 = 0,85 мм.

При решении обратной задачи — по допуску замыкающего звена определить допуски остальных звеньев — сталкиваются с математической неопределенностью (при m>2); в этом случае определяют средний допуск всех звеньев

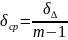
где _ —допуск замыкающего звена;

m — число всех звеньев в цепи

Величина среднего допуска изменяется в сторону увеличе­ния или уменьшения в зависимости от назначения и функции звеньев, их геометрических размеров, формы, материала и пр. Сумма всех корректированных допусков должна равняться _. Чем больше звеньев в цепи, тем меньше _ср и тем точнее долж­ны быть изготовлены детали. Решение размерной цепи в ко­нечном счете сводится к получению равенства основного уравнения , которое обеспечивает заданную точность соединения и координиро­вание деталей в узле и узлов в станке. Как отмечалось выше, для получения необходимой точности соединения деталей станков существует пять методов решения размерных цепей: полной взаимозаменяемости, непол­ной (частичной) взаимоза­меняемости, групповой вза­имозаменяемости, пригонки, регулирования или сборки с компенсаторами (с помо­щью подвижного и непод­вижного компенсатора).

При сборке по методу полной взаимозаменяемости расчет цепи выполняется в следующем порядке:

1. Составляют размерные цепи и определяют размеры замы­кающих звеньев.

2. Устанавливают величину допуска на размер замыкаю­щего звена в зависимости от назначения механизма и техниче­ских условий.

3. Определяют в зависимости от допуска замыкающего зве­на среднюю величину допусков всех звеньев размерной цепи по формуле

4. Корректируют среднюю величину допуска на размер для каждого звена с учетом размеров деталей, их конструктивных особенностей и технологических возможностей получения необ­ходимой точности при их обработке.

5. Производят проверочный расчет правильности установ­ленных допусков на размеры для каждого звена по формуле

К преимуществам этого метода сборки относятся: 1) полу­чение заданной точности замыкающего звена вследствие точно­сти изготовления составляющих звеньев, сумма допусков кото­рых не выходит за пределы допуска замыкающего звена, реше­ние размерной цепи сводится к соединению составляющих ее звеньев; 2) возможность проведения сборки узлов или станка рабочими невысокой квалификации; 3) низкая стоимость и про­стая организация процесса сборки; 4) простота ремонта стан­ка, так как вследствие использования взаимозаменяемых запасных деталей, изготовленных с заданной точностью, они могут быть установлены на станок без пригонки по месту.

Недостатком сборки по методу полной взаимозаменяемости является высокая стоимость изготовления оснастки для изготов­ления деталей и сборки, вследствие чего сборка по этому ме­тоду применяется в массовом и крупносерийном производстве.

Применение метода неполной взаимозаменяемости при сборке станков возможно путем увеличения допусков на отдель­ные звенья цепи с учетом вероятностей отклонений размеров звеньев, составляющих размерную цепь. В этом случае нет гарантии, что точность размерной цепи уложится в заданные пределы допуска замыкающего звена _, т. е. имеется опасение несовпадения размеров; процент этого несовпадения характе­ризует степень приближения частичной взаимозаменяемости к полной. Обработка детали вследствие увеличения допусков звеньев размерных цепей упрощается.

Расчет цепи производится с учетом ошибки несовпадения замыкающего звена, выходящего за пределы допуска.

Средняя величина допуска _ср определяется по формуле

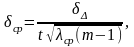
где _ср — средняя величина допуска для всех звеньев данной цепи;

_ — допуск замыкающего звена;

t —коэффициент риска, принимаемый в зависимости от установленного процента риска, приведенного ниже;

_ср — коэффициент рассеяния, зависящий от формы кри­вой распределения ошибок каждого из звеньев раз­мерной цепи, если все они подчиняются одному за­кону, определяемый по табл. 32.

Сборка по методу групповой взаимозаменяемости. В станко­строении метод подбора при сборке находит применение глав­ным образом при решении малозвенных размерных цепей, имеющих высокую точность, например при сборке шпинделей и подшипников по отверстиям корпусов и др. Расчет величины экономичных производственных допусков на механическую об­работку деталей производится по формуле

_пр = n,

где _пр – экономический производственный допуск отверстия или вала;

 – допуск отверстия или вала, соответствующих усло­виям сборки;

n – число групп, на которое разбиваются детали каждо­го наименования, выполненные с производственным допуском.

Таблица 32 – Значения коэффициента  при различных законах распределения ошибок звеньев размерной цепи

Закон распределения								Условия применения
Равной вероятности					1/3			m – 1  6
Треугольный					1/6			m – 1  4
Нормальный					1/9			m – 1  3
Процент риска	0,27	0,60	1,0	2,0		4,0	6,0		8,0	10,0	33,0
t	3,0	2,70	2,57	2,34		2,06	1,88		1,75	1,65	1,00

Предположим, необходимо получить сопряжение шпинделя и подшипника d = 80 мм, которое должно быть изготовлено с точностью 0,01 мм. Изготовить отверстие подшипника и шпин­дель с точностью 0,005 мм вызывает затруднения.

Допустим, что указанные детали будут изготовлены по тех­нологически возможным расширенным допускам, соответствую­щим 2-му классу точности. Тогда допуск на отверстие и вал

_А = + 0,035 мм, _В = – 0,023 мм;

суммарный допуск  = _А + _В = 0,035 + 0,023 = 0,058 мм; при групповом допуске соединения 0,01 мм число групп будет

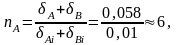
т. е. необходимо разбить расширенные поля допусков на шесть групп, где _Аi и _Вi — допуски составляющих звеньев — отвер­стия и вала цепи. Разбивка деталей по группам производится при помощи ступенчатых калибров (рис. 147, б). Недостатком метода групповой сборки является большое незавершенное про­изводство, необходимость дополнительных обмеров, сортировки и клеймения деталей, четкой организации их хранения и достав­ки на рабочие места.

Метод пригонки при сборке деталей применяется в тех случаях, когда по условиям работы меха­низма требуемая точность настолько высока, что допуски основных разме­ров деталей, образующих размерную цепь, технологически выполнить труд­но. В этом случае детали изготовляют по размерам с расширенными допуска­ми, а требуемая точность механизма при сборке достигается пригонкой.

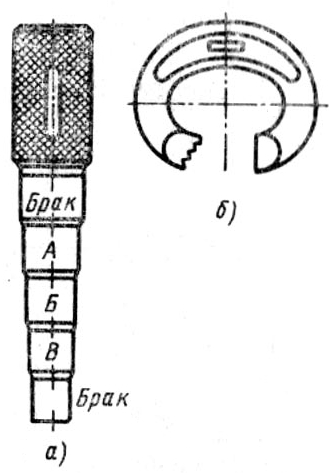
Рис. 147 Калибры для сортировки деталей на три группы: а – пробка, б – скоба

Применение этого метода при сбор­ке станков позволяет обеспечить равен­ство основного уравнения размерной цепи путем изменения размера одного из его звеньев, осуществляемого с целью компенсации ошибки, превыша­ющей допустимую и нарушающей ука­занное равенство. Это достигается подгонкой или изготовлением звена по месту. При изменении размеров такого звена сохраняется основное уравнение группы: размерной цепи, т. е. заданная точность сборки, называется компенси­рующей. Расчет величины ошибок компенсирующего звена определяется по формуле

,

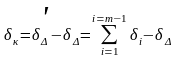где _к — величина компенсации;

_ — величина погрешности замыкающего звена, получен­ная при расширенных допусках всех звеньев;

_ — допустимая величина погрешности замыкающего звена;

_i — величина расширенных допусков звеньев размерной цепи;

m — общее количество всех звеньев размерной цепи, включая и замыкающее звено. Например, для размерной цепи (соединение шпонка шпоночный паз) пригонка в этом случае может быть осуществлена снятием припуска с компенсирующе­го звена (рис. 148). Для обеспечения заданного допуска замыкающего звена _ при сборке по методу полной взаимозаменяе­мости уравнение размерной цепи имеет вид (рис. 148, а)

_ =₁ + ₂,

где _ — заданная точность размерной цепи;

₁ — допуск на ширину шпоночного паза;

₂ — допуск на ширину шпонки.

В случае же пригонки заданные ранее допуски расширяют до величин ₁ и ₂ (рис. 148, б).

Компенсирующим является то звено, которое легче при­гнать. В данном случае та­ким звеном является шири­на Б шпонки, которая дол­жна быть увеличена на ве­личину компенсации, рав­ную

_к =_ - _,

следовательно, новый размер будет Б₁=Б + _к

Метод пригонки приме­няется в условиях индиви­дуального и мелкосерийно­го производства. Он широ­ко распространен и при ре­монте станков. Основное его преимущество заключается в возможности получения требуемой точности сборки при сравнительно широких допусках на звенья размерной цепи. В процессе пригонки проверяется правильность размеров и по­ложение компенсирующих деталей относительно деталей, сопря­женных с ними.

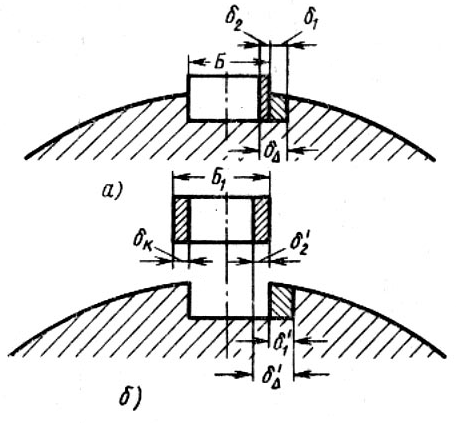
Рис. 148 Схема сборки шпонки с валом: а – по методу полной взаимозаменяемости; б – по методу пригонки