
- •Лекция 1
- •1. Запись чисел в десятичной системе счисления. Теорема о существовании и единственности десятичной записи натурального числа.
- •2. Теорема о сравнении натуральных чисел по их десятичной записи. Образование названий и запись натуральных чисел.
- •3.Сложение чисел в десятичной системе счисления. Алгоритм сложения.
- •4. Вычитание натуральных чисел в десятичной системе счисления.
- •8. Умножение натуральных чисел в десятичной системе счисления.
- •9. Деление натуральных чисел в десятичной системе счисления.
- •10. Позиционные системы счисления, отличные от десятичной.
- •1. Отношение делимости во множестве целых неотрицательных чисел, его основные
- •2. Признаки делимости.
- •3. Нод и нок чисел, их свойства. Пункт 1. Общий делитель и наибольший общий делитель.
- •Пункт 2. Свойства нод.
- •Пункт 3. Взаимнопростые числа.
- •Пункт 4. Наименьшее общее кратное целых чисел.
- •4. Признак делимости на составное число.
- •5. Простые и составные числа. Свойства простых чисел.
- •П.2. Основные свойства простых и составных чисел
- •6. «Решето Эратосфена».
- •7. Основная теорема арифметики.
- •8. Алгоритм Евклида. Алгоритм Евклида и нод двух целых чисел.
1. Отношение делимости во множестве целых неотрицательных чисел, его основные
Z является областью целостности, поэтому все утверждения, определения, которые сформулированы для произвольной области целостности справедливы и для кольца Z.
Определение
1. Пусть
![]() Будем говорить, что
делится на
и обозначать
Будем говорить, что
делится на
и обозначать
![]() {или
{или
![]() }
тогда и только тогда, когда найдется
такое
}
тогда и только тогда, когда найдется
такое
![]() ,
что
,
что
![]() .
При этом
- делимое,
- делитель,
.
При этом
- делимое,
- делитель,
![]() - частное.
- частное.
Синонимы: 1) кратно ;
2) делит ;
3) делитель .
Предложение 1. Частное от деления на определяется однозначно.
Доказательство
проведем методом от противного.
Предположим, что существует два частных
от деления
на
:
![]() и
и ![]() .
Тогда
.
Тогда ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() . В силу монотонности операции умножения
получаем, что
. В силу монотонности операции умножения
получаем, что ![]() .
Таким образом мы получили противоречие
с нашим предположением. Следовательно
оно не верно и частное от деления двух
целых чисел определяется однозначно.
Предложение доказано.
.
Таким образом мы получили противоречие
с нашим предположением. Следовательно
оно не верно и частное от деления двух
целых чисел определяется однозначно.
Предложение доказано.
Основные свойства:
 ,
,
 ;
;
Доказательство:
Поскольку ![]() ,
то
,
то
![]() .
.
 ;
;
Доказательство:
![]() ,
,
![]() .
Тогда
.
Тогда ![]() .
Поскольку
,
то
.
Поскольку
,
то ![]() .
Следовательно,
.
Следовательно, ![]() ,
то есть
,
то есть ![]() .
.
 ;
;
Доказательство:
,
![]() .
Тогда
.
Тогда ![]() .
Так как
.
Так как ![]() ,
то
,
то ![]() .
Следовательно,
.
Следовательно, ![]() или
или ![]() .
.
 ;
;
Доказательство:
![]() ,
.
Тогда
,
.
Тогда ![]() .
Следовательно,
.
Следовательно, ![]() или
или ![]() .
.
 ;
;
Доказательство:
.
Тогда ![]() .
Так как
.
Так как ![]() ,
то
,
то ![]() .
Следовательно,
.
Следовательно, ![]() .
.
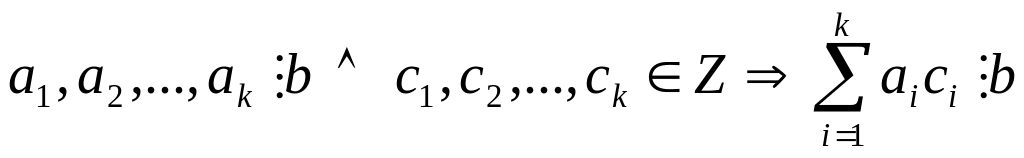 ;
;
Доказательство следует из свойств 4 и 5.
 ;
;
Доказательство:
![]()
![]()
![]()
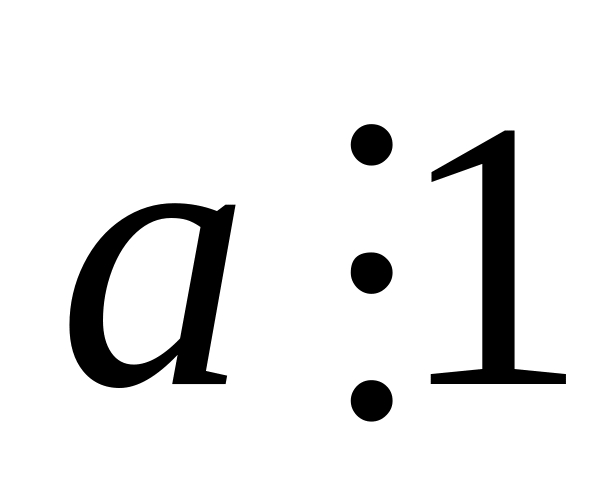 ;
;
Доказательство:
Поскольку ![]() ,
то
,
то ![]() .
Следовательно,
.
Следовательно, ![]() .
.
 ;
;
Доказательство:
Поскольку ![]() ,
то
,
то ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Деление на 0 невозможно.
Доказательство:
Пусть
![]() .
Тогда по определению
.
Тогда по определению
![]() .
Этому равенству удовлетворяет каждое
натуральное число. Это противоречит
теореме об однозначности частного.
Следовательно, деление нуля на ноль
невозможно. Пусть теперь
.
Этому равенству удовлетворяет каждое
натуральное число. Это противоречит
теореме об однозначности частного.
Следовательно, деление нуля на ноль
невозможно. Пусть теперь
![]() .
Тогда по определению
.
Тогда по определению
![]() .
Произведение любого числа на ноль равно
нулю, но
.
Получили противоречие. Следовательно,
деление на ноль невозможно.
.
Произведение любого числа на ноль равно
нулю, но
.
Получили противоречие. Следовательно,
деление на ноль невозможно.
Если
 ,
то
,
то
 .
.
Доказательство:
Пусть
![]() .
Тогда согласно свойству 7.
.
Тогда согласно свойству 7.
![]() .
Поэтому мы можем сказать, что
.
Поэтому мы можем сказать, что
![]() .
По определению
.
По определению
![]() ,
где
,
где
![]() - натуральное число, то есть
может быть равно 1 и тогда
- натуральное число, то есть
может быть равно 1 и тогда
![]() ,
либо
может быть больше 1 и тогда
,
либо
может быть больше 1 и тогда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
2. Признаки делимости.
Теорема 1 (общий признак делимости Паскаля).
Пусть
![]() записано в десятичной системе счисления:
записано в десятичной системе счисления:
![]() ,
,![]() , тогда
, тогда
![]()
![]() -
цифры числа
-
цифры числа
![]() в десятичной системе счисления,
в десятичной системе счисления,
![]() .
.
![]() -
наименьшие по абсолютной величине
вычеты числа
-
наименьшие по абсолютной величине
вычеты числа
![]() ,
по модулю
.
,
по модулю
.
Доказательство:
Запишем натуральное число
![]() в десятичной системе счисления следующим
образом:
.
в десятичной системе счисления следующим
образом:
.
Найдем ряд остатков по следующей схеме:
—
остаток от деления 10
на ![]() ;
;
![]() —
остаток от деления
—
остаток от деления ![]() на
;
на
;
![]() — остаток от деления
— остаток от деления ![]() на
;
на
;
…
![]() — остаток от деления
— остаток от деления ![]() на
.
на
.
Так
как остатков конечное число (а именно
),
то этот процесс зациклится не позже,
чем через
шагов и дальше можно его не продолжать:
Начиная с некоторого ![]() ,
,
![]() где
где ![]() — получившийся период последовательности
— получившийся период последовательности
![]() .
Для единообразия можно принять, что
.
Для единообразия можно принять, что
![]() .
.
Тогда
![]() имеет тот же остаток от деления на
,
что и число
имеет тот же остаток от деления на
,
что и число ![]() .
.
Следствие
1.
Число
делится на 2 тогда и только тогда, когда
последняя его цифра
![]() делится
на 2.
делится
на 2.
Следствие 2. Число делится на 5 тогда и только тогда, когда последняя его цифра делится на 5.
Следствие
3.
Число
делится на 3 тогда и только тогда, когда
![]() делится
на 3.
делится
на 3.
Следствие 4. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Следствие 5. Число делится на 4 тогда и только тогда, когда число, составленное двумя последними цифрами данного числа , делится на 4.
Следствие 6. Число делится на 25 тогда и только тогда, когда число, составленное двумя последними цифрами данного числа , делится на 25.
Следствие
7.
Число
делится на 11 тогда и только тогда, когда
![]() .
.
Замечание 1. Подобным образом можно получить признак делимости на любое натуральное число.
Замечание 2. Признаки делимости можно получить в любой системе счисления.
