10. Позиционные системы счисления, отличные от десятичной.

Основанием позиционной системы счисления может быть не только число 10, но и вообще любое натуральное число . Система счисления с основанием называется -ичной. Так, если , то – двоичной, если - восьмеричной, если - десятичной.

Для записи чисел в системе с основанием необходимо символов. Принято использовать знаки десятичной системы счисления: . Например, числа в троичной системе счисления записывают при помощи символов , а в пятеричной - при помощи символов .

Определение. Записью натурального числа х в системе счисления с основанием называется его представление в виде: (1), где коэффициенты принимают значения и .

Теорема. Пусть - заданное натуральное число. Тогда любое натуральное число представимо, и при том единственным образом в виде (1).

Вместо представления в виде (1) число записывают кратко: . Например, если , то число можно записать в виде , причем читать его следует так: «Два, ноль, один, два в троичной системе счисления».

Задача. Сосчитать число клеток в фигуре, изображенной на рисунке, в троичной системе счисления.

Решение. В троичной системе счисления для записи чисел используются цифры 0,1 и 2, а любое число представляется в виде , где принимают значения , а число 3 – основание системы счисления – записывается как 10.

При счете клеток в данной фигуре мы получим числа, запись и называние которых в троичной системе счисления таковы: 1 (один); 2 (два); 10 (один, ноль); 11 (один, один); 12 (один, два); 20 (два, ноль); 21 (два, один); 22 (два, два); 100 (один, ноль, ноль).

Таким образом, число клеток в фигуре на рисунке в троичной системе счисления запишется как .

В пятеричной системе счисления для записи чисел используются цифры , а любое число представляется в виде , где принимают значения и .

Однозначные числа в этой системе - , а число 5 – основание системы счисления – записывается как 10.

При счете в пятеричной системе клеток фигуры на рисунке мы получим числа: 1,2,3,4,10,11,12,13,14. Таким образом, число этих клеток в пятеричной системе счисления запишется как .

Сравнение чисел в системе счисления с основанием ( ) выполняется также, как и в десятичной системе. Так, , поскольку при одинаковом числе разрядов и совпадении трех цифр старших разрядов число единиц в первом числе меньше числа единиц во втором.

Арифметические действия над числами в позиционных системах счисления с основанием ( ) выполняются по тем же правилам, что и в десятичной системе счисления. Надо лишь иметь для системы с основанием соответствующие таблицы сложения и умножения однозначных чисел.

Составим, например, таблицу сложения однозначных чисел в троичной системе счисления. Однозначные числа в ней – это 0,1,2. Число 3 записывается 10. Число 4 имеет вид , так как .

Полностью таблицу сложения однозначных чисел в троичной системе счисления можно представить в таком виде:

	0	1	2
0	0	1	2
1	1	2	10
2	2	10	11

Используя эту таблицу, можно складывать любые числа в троичной системе счисления, причем многозначные числа можно складывать столбиком по правилам, аналогичным правилам сложения чисел в десятичной системе счисления. Например, , так как

Таблицей сложения однозначных чисел в троичной системе счисления можно пользоваться, выполняя вычитание: .

Таблица умножения однозначных чисел в троичной системе счисления имеет вид:

	0	1	2
0	0	0	0
1	0	1	2
2	0	2	11

На основе этой таблицы и таблицы сложения выполняют умножение многозначных чисел по правилам, аналогичным правилам умножения чисел в десятичной системе счисления. Найдем, например, произведение :

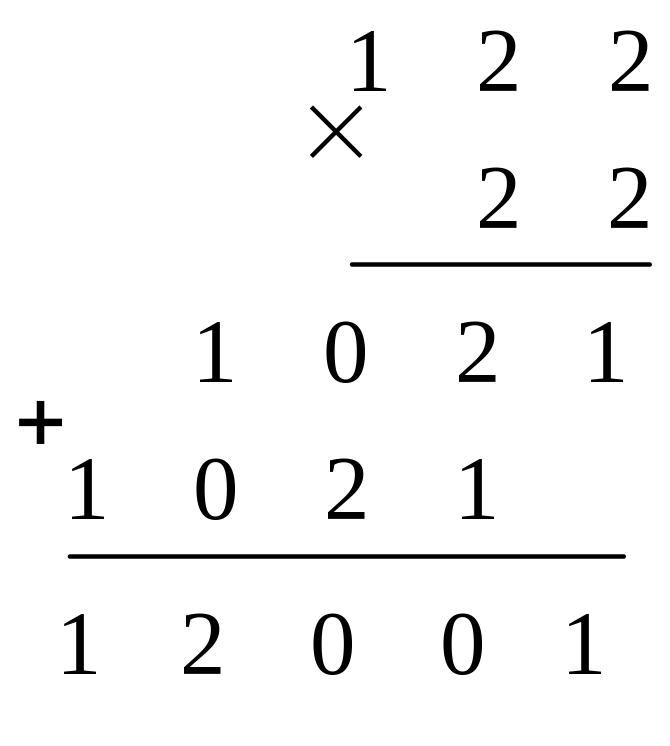
Таким образом, .

Таблицей умножения можно пользоваться, выполняя деление в троичной системе счисления, в частности, деление чисел уголком. Разделим, например, число на :

Значит, .

Одно и то же натуральное число может быть записано в любой системе счисления с основанием . Так, число клеток в фигуре на рисунке в десятичной системе счисление записывается знаком 9, в троичной – 100, в пятеричной – 14.

Чтобы из одной записи получить другую, достаточно научиться переходить от записи в заданной системе к записи в десятичной, и наоборот.

Пусть дана запись числа в системе счисления с основанием , то есть . Найдем запись этого числа в десятичной системе счисления. Так как в записи числа числа и представлены в десятичной системе счисления, то, выполнив над ними действия по правилам, принятым в ней, получим десятичную запись числа . Найдем, например, десятичную запись числа . Для этого представим данное число в виде суммы вида: . Значение этого выражения в десятичной системе счисления равно 303. Следовательно, .

Пусть теперь число записано в десятичной системе. Найдем его запись в системе счисления с основанием .

Число можно записать в виде . Так как , то из последней записи числа видно, что - остаток, получаемый при делении этого неполного частного на . Таким образом, запись числа в -ичной системе находят так: число делят (в десятичной системе) на ; остаток, полученный при делении, даст последнюю цифру в -ичной записи числа ; неполное частное снова делим на , новый остаток даст предпоследнюю цифру -ичной записи числа ; продолжая деление, найдем все цифры -ичной записи числа .

Запишем число 2436 в восьмеричной системе счисления. Разделим 2436 на 8: . При делении числа 304 на 8 получим: или . Делим на 8 число 38: и тогда , то есть . Описанный процесс можно представить и в таком виде: