8. Умножение натуральных чисел в десятичной системе счисления.

Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в таблицу умножения и запоминают.

Умножение многозначного числа на однозначное основывается на:

- записи чисел в десятичной системе счисления;

- свойствах сложения и умножения;

- таблицах сложения и умножения однозначных чисел.

Правило умножения многозначного числа на однозначное:

Пусть требуется умножить на однозначное число : . Воспользуемся дистрибутивностью умножения относительно сложения: . Используем коммутативное свойство умножения:

. Используем ассоциативное свойство умножения: . После этого, используя таблицу умножения, заменяем все произведения , где , соответствующими значениями и получаем:

.

По таблице сложения заменяем суммы , где и , их значениями. Если, например, однозначно, то последняя цифра произведения равна . Если же , то последняя цифра равна , а к скобке надо прибавить 1. Продолжая этот процесс, получим десятичную запись числа .

Пример1:

Вычислим:

Представим первое число в десятичной записи:

Воспользуемся дистрибутивностью умножения относительно сложения:

Используем коммутативное свойство умножения:

Используем ассоциативное свойство умножения:

Заменяем все произведения , где , соответствующими значениями :

Используя ассоциативное свойство сложения и дистрибутивность умножения относительно сложения, приведем подобные:

По таблице сложения заменяем суммы , где и , их значениями:

Запишем произведение в виде краткой записи:

.

Алгоритм умножения многозначного числа на однозначное:

1. Записать второе число под первым.

2. Умножить цифры разряда единиц числа на число . Если произведение меньше 10, записать его в разряд единиц ответа и перейти к следующему разряду (десятков).

3. Если произведение цифры единиц числа на число больше или равно 10, то представить его в виде , где - однозначное число; записать в разряд единиц ответа и запоминаем 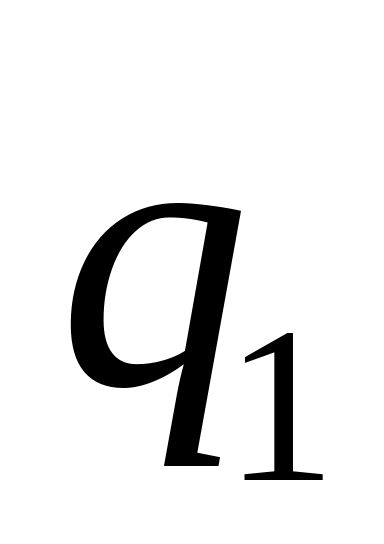- перенос в следующий разряд.

4. Умножить цифру разряда десятков числа на число , прибавить к полученному произведению число и повторяем процесс, описанный в пунктах 2 и 3.

5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда.

Пример2:

Вычислим:

1) Запишем второе число под первым: .

2) Умножим 7 на 4. Получим . Представим 28 в виде . Запишем 8 в разряд единиц ответа и запомним 2: .

3) Умножим 5 на 4 и прибавим к произведению 2. Получим . Представим 22 в виде . Запишем 2 в разряд сотен ответа и запомним 2: .

4) Умножим 3 на 4 и прибавим к произведению 2. Получим . Представим 14 в виде . Запишем 4 в разряд тысяч ответа и запомним 1: .

5) Добавим 0 в разряд десятков тысяч числа 357. Умножим 0 на 4 и прибавим к произведению 1. Получим . Запишем 1 в разряд десятков тысяч ответа: .

Умножение многозначного числа на многозначное основывается на:

- умножении многозначного числа на однозначное и на степень десяти;

- сложении многозначных чисел.