4. Вычитание натуральных чисел в десятичной системе счисления.

Вычитание однозначного числа из однозначного или двузначного числа , не превышающего 18, сводится к поиску такого числа , что , и происходит с учетом таблицы сложения однозначных чисел.

В основе алгоритма вычитания многозначного числа из многозначного числа лежат следующие теоретические факты:

- способ записи чисел в десятичной системе счисления;

- правилах вычитания числа из суммы и суммы из числа;

- дистрибутивность умножения относительно сложения;

- таблица сложения однозначных чисел.

Правило вычитания многозначного числа из многозначного числа:

Пусть даны числа: и . Известно также, что .

Рассмотрим разность:

.

Воспользуемся правило вычитания суммы из числа:

.

Воспользуемся правило вычитания числа из суммы:

.

Воспользуемся дистрибутивностью умножения относительно сложения:

. (1)

Эта формула задает алгоритм вычитания только при условии, что для всех выполняется условие . Если же это условие не выполняется, то берем наименьшее , для которого . Пусть - наименьший индекс, такой, что и , а . Тогда имеет место равенство

(например, если , то ). Поэтому в равенстве (1) выражение можно заменить на

. Из того, что , вытекает неравенство , а из того, что , вытекает неравенство , где . Поэтому в записи

Все коэффициенты с индексом, меньшим , неотрицательны и не превосходят 9. Применяя далее те же преобразования к коэффициентам , через шагов придем к записи разности в виде , где для всех выполняется неравенство . Если при этом окажется, что , то надо отбросить первые слагаемые, вплоть до первого коэффициента, отличного от нуля.

Пример1:

Вычислим:

Представим числа в десятичной записи:

Воспользуемся правилом вычитания суммы из числа:

Воспользуемся правилом вычитания суммы из числа

Воспользуемся дистрибутивностью умножения относительно сложения:

Так как , то представим в виде .

Получим:

Вычислим разность однозначных чисел в соответствующих разрядах:

Запишем разность в виде краткой записи:

.

Алгоритм вычитания:

1. Записать вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.

2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, вычесть ее из цифры вычитаемого, записать разность в разряд единиц ответа, после чего перейти к следующему разряду.

3. Если цифра в разряде единиц вычитаемого больше единиц уменьшаемого, то есть 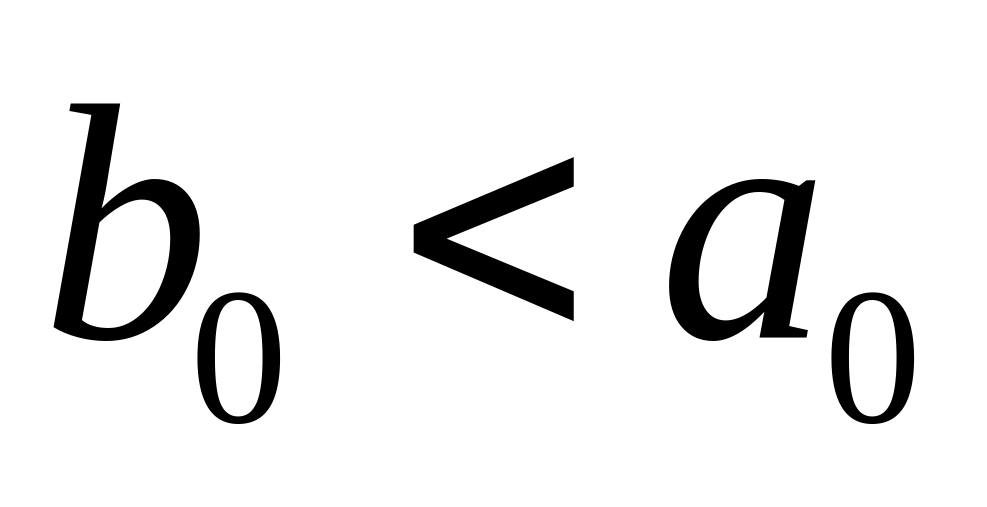, а цифра десятков уменьшаемого отлична от нуля, то уменьшить цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычесть из числа 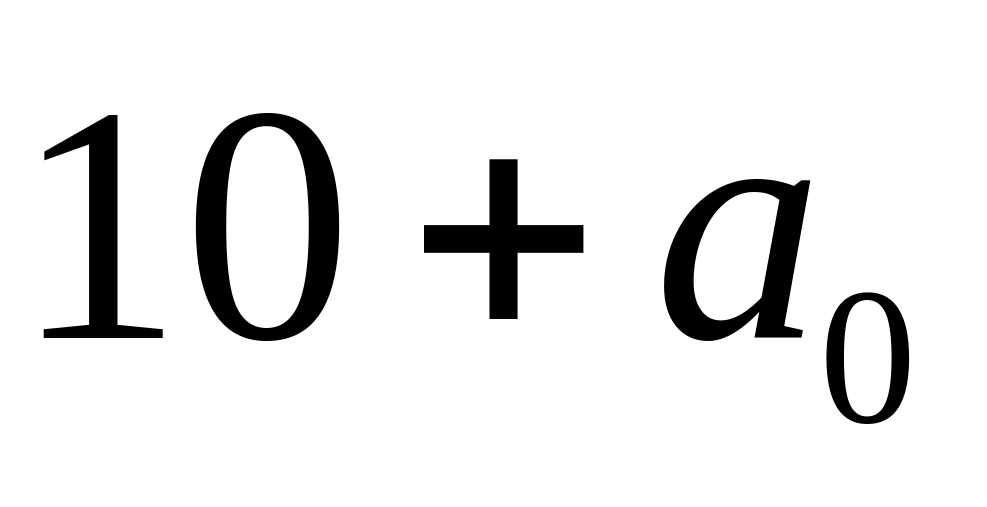число и записать разность в разряде единиц ответа, далее перейти к следующему разряду.

4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, стоящие в разряде десятков, сотен и так далее уменьшаемого, равны нулю, то взять первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшаем ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличить на 9, а цифру в разряде единиц на 10: вычесть из , записать разность в разряде единиц ответа и перейти к следующему разряду.

5. В следующем разряде повторяем описанный процесс.

6. Вычитание заканчивается, когда производится вычитание из старшего разряда уменьшаемого.

Пример2:

Вычислим:

1) Запишем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.

2) Так как , то уменьшим цифру десятков уменьшаемого на 1, увеличив при это 7 на 10, и вычтем 8 из 17:

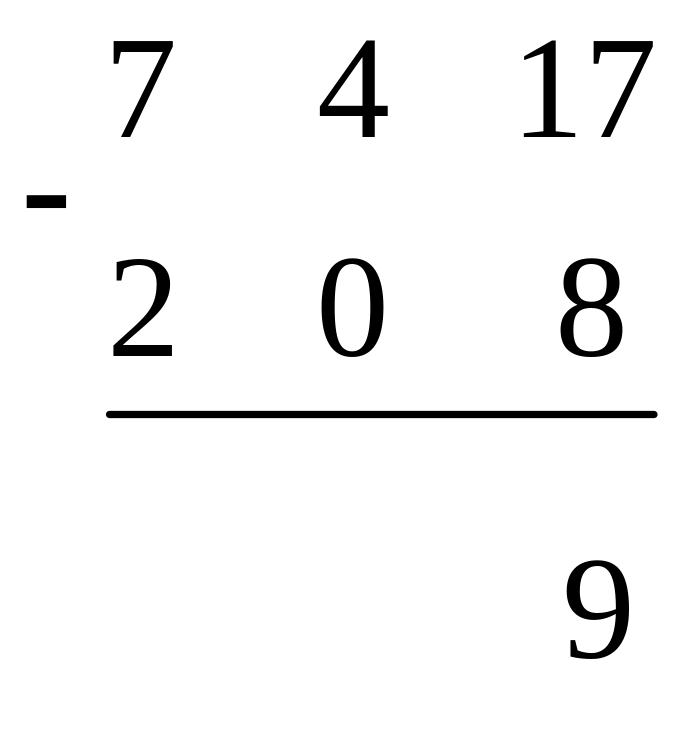
3) Вычтем 0 из 4:

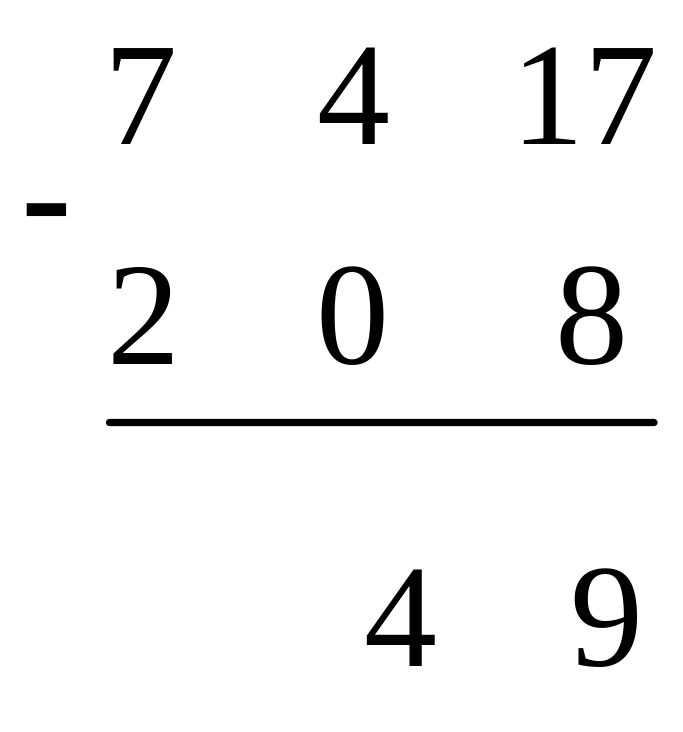
4) Вычтем 2 из 7:

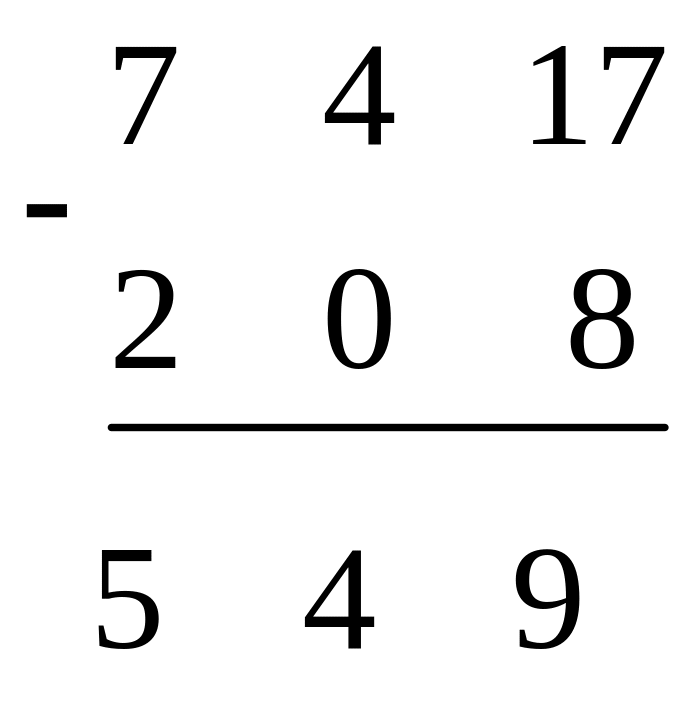
Ответ: .