5. Простые и составные числа. Свойства простых чисел.

п.1. Простое и составное число

Определение 1. а, принадлежащее Z , отличное от ±1, 0, называется простым, если оно делится только лишь на ±1,±а.

Определение 2. m, принадлежащее Z, отличное от ±1, 0, называется составным, если оно имеет хотя бы один делитель отличный от ±1, ±m.

Далее будем рассматривать простые натуральные числа.

Определение 1’. р, принадлежащее N, отличное от 1, называется простым, если р делится только лишь на 1, р.

Определение 2’. n, принадлежащее N, отличное 1, называется составным, если имеет хотя бы один делитель, отличный от 1, n.

П.2. Основные свойства простых и составных чисел

1. Пусть n – натуральное, отличное от 1, р – простое и , тогда р = n.

2. Пусть р1, р2 – простые, р1 ≠ р2, тогда р1 не делится на р2 и р2 не делится на р1.

3. Всякое натуральное n>1 имеет хотя бы один простой делитель.

4. Если n – натуральное, р – простое, тогда либо НОД(n,р)=1, либо n делится на р.

5. Если а, в – натуральные и 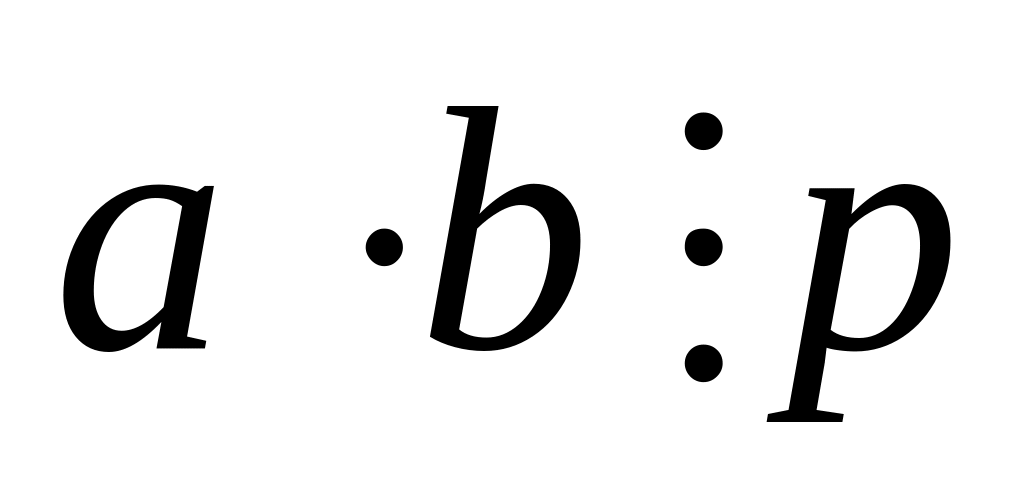, тогда 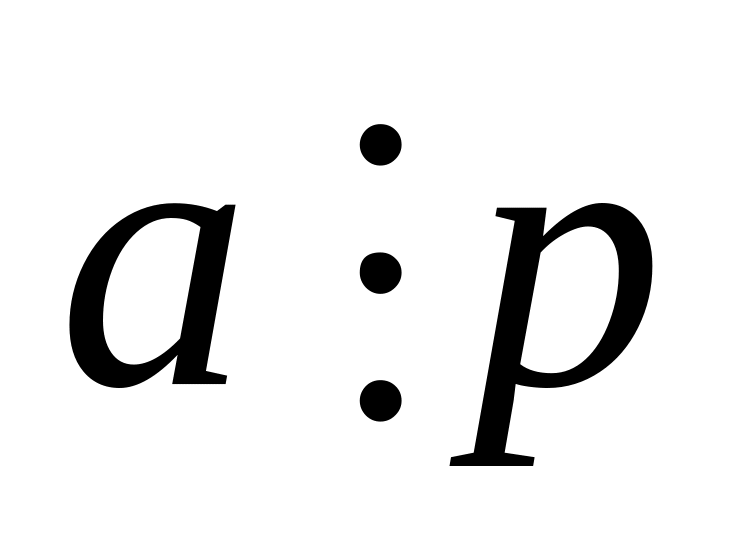или .

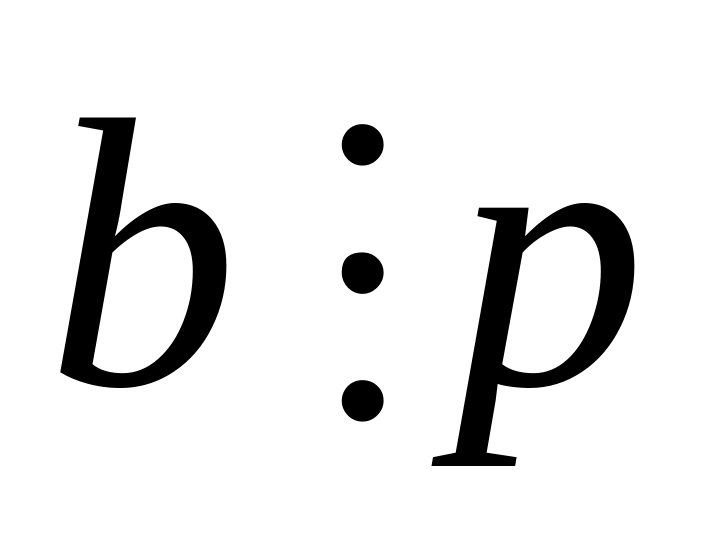6. Наименьший простой делитель р (n делится на р, р – простое, n – составное) не превосходит .

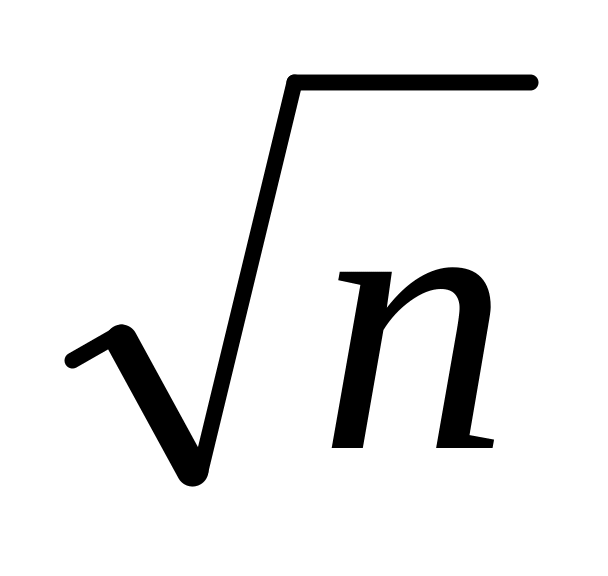7. Свойство Евклида. Множество простых чисел бесконечно.

8. Существуют интервалы сколь угодно большой длины, в которых нет ни одного простого числа.

6. «Решето Эратосфена».

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).

Пусть переменная p изначально равна двум — первому простому числу.

Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)

Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.

Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n/2

Все не вычеркнутые числа в списке — простые числа.

На практике, алгоритм можно значительно улучшить следующим образом. На шаге №3, числа можно вычеркивать, начиная сразу с числа p2, потому что все составные числа меньше его уже будут вычеркнуты к этому времени. И, соответственно, останавливать алгоритм нужно, когда p2 станет больше, чем n.

7. Основная теорема арифметики.

Теорема (Основная теорема арифметики)

Всякое натуральное число n>1 либо простое, либо его можно представить в виде произведения простых сомножителей и при том однозначно с точностью до порядка следования сомножителей.

Доказательство.

Если простое число p делит без остатка произведение двух целых чисел , то p делит x или y.

Существование. Пусть n — наименьшее натуральное число, неразложимое в произведение простых чисел. Оно не может быть единицей по формулировке теоремы. Оно не может быть и простым, потому что любое простое число является произведением одного простого числа — себя. Если n составное, то оно — произведение двух меньших натуральных чисел. Каждое из них можно разложить в произведение простых чисел, значит, n тоже является произведением простых чисел. Противоречие.

Единственность. Пусть n — наименьшее натуральное число, разложимое в произведение простых чисел двумя разными способами. Если оба разложения пустые — они одинаковы. В противном случае, пусть p — любой из сомножителей в любом из двух разложений. Если p входит и в другое разложение, мы можем сократить оба разложения на p и получить два разных разложения числа n / p, что невозможно. А если p не входит в другое разложение, то одно из произведений делится на p, а другое — не делится (как следствие из леммы Евклида, см. выше), что противоречит их равенству.

Определение 3. Представление натурального числа n в виде ,где - различные простые числа. называется каноническим представлением.

Основная теорема арифметики утверждает, что каждое натуральное число n > 1 представляется в виде n = p1 · p2 · p3 · p4 · p5 · .... · pk , где p1 , ...., pk — простые числа, причём такое представление единственно с точностью до порядка следования сомножителей.