
Линейная модель
Уравнение линейной регрессии имеет вид: y=a + b*x, где a и b-коэффициенты регрессии(неизвестные параметры). С помощью метода наименьших квадратов, выводим формулы для вычисления неизвестных параметров, которая имеет вид:
a=![]()
b=
![]() отсюда
отсюда
a=(131,4*16265,4-126,84*16835,92)/(16265,4-16088,39)=10,19955
b=(16835,92-126,84*131,4)/(16265,4-16088,39)=0,955538
y |
x |
y^2 |
x^2 |
x*y |
y(т) |
y(т)-y |
|y(т)-y| |
(|y(т)-y|)/y |
|
150 |
140 |
22500 |
19600 |
21000 |
143,9749 |
-6,02512 |
6,025119 |
0,040167 |
|
137 |
130 |
18769 |
16900 |
17810 |
134,4195 |
-2,5805 |
2,5805 |
0,018836 |
|
130 |
125 |
16900 |
15625 |
16250 |
129,6418 |
-0,35819 |
0,35819 |
0,002755 |
|
147 |
145 |
21609 |
21025 |
21315 |
148,7526 |
1,752572 |
1,752572 |
0,011922 |
|
120 |
115 |
14400 |
13225 |
13800 |
120,0864 |
0,086429 |
0,086429 |
0,00072 |
|
142 |
139 |
20164 |
19321 |
19738 |
143,0193 |
1,019343 |
1,019343 |
0,007178 |
|
149 |
147 |
22201 |
21609 |
21903 |
150,6636 |
1,663648 |
1,663648 |
0,011165 |
|
123 |
120 |
15129 |
14400 |
14760 |
124,8641 |
1,86412 |
1,86412 |
0,015155 |
|
131 |
123 |
17161 |
15129 |
16113 |
127,7307 |
-3,26927 |
3,269266 |
0,024956 |
|
119 |
110 |
14161 |
12100 |
13090 |
115,3087 |
-3,69126 |
3,691261 |
0,031019 |
|
111 |
105 |
12321 |
11025 |
11655 |
110,531 |
-0,46895 |
0,468952 |
0,004225 |
|
139 |
135 |
19321 |
18225 |
18765 |
139,1972 |
0,197191 |
0,197191 |
0,001419 |
|
125 |
122 |
15625 |
14884 |
15250 |
126,7752 |
1,775196 |
1,775196 |
0,014202 |
|
135 |
130 |
18225 |
16900 |
17550 |
134,4195 |
-0,5805 |
0,5805 |
0,0043 |
|
107 |
101 |
11449 |
10201 |
10807 |
106,7089 |
-0,2911 |
0,291104 |
0,002721 |
|
115 |
113 |
13225 |
12769 |
12995 |
118,1754 |
3,175353 |
3,175353 |
0,027612 |
|
124 |
119 |
15376 |
14161 |
14756 |
123,9086 |
-0,09142 |
0,091419 |
0,000737 |
|
133 |
129 |
17689 |
16641 |
17157 |
133,464 |
0,463962 |
0,463962 |
0,003488 |
|
138 |
136 |
19044 |
18496 |
18768 |
140,1527 |
2,152729 |
2,152729 |
0,015599 |
|
148 |
144 |
21904 |
20736 |
21312 |
147,797 |
-0,20297 |
0,202967 |
0,001371 |
|
110 |
107 |
12100 |
11449 |
11770 |
112,4421 |
2,442124 |
2,442124 |
0,022201 |
|
132 |
128 |
17424 |
16384 |
16896 |
132,5084 |
0,508424 |
0,508424 |
0,003852 |
|
146 |
142 |
21316 |
20164 |
20732 |
145,886 |
-0,11404 |
0,114043 |
0,000781 |
|
148 |
145 |
21904 |
21025 |
21460 |
148,7526 |
0,752572 |
0,752572 |
0,005085 |
|
126 |
121 |
15876 |
14641 |
15246 |
125,8197 |
-0,18034 |
0,180342 |
0,001431 |
|
3285 |
3171 |
435793 |
406635 |
420898 |
|
|
|
0,2729 |
Сумма |
131,4 |
126,84 |
17431,72 |
16265,4 |
16835,92 |
|
|
|
|
Ср. знач. |
17265,96 |
16088,39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
r |
A |
F |
Э |
|
|
|
|
10,19955 |
0,955538 |
0,987444 |
1,091599 |
898,6755 |
0,922378 |
|
|
|
|
|
|
0,975045 |
|
|
|
|
|
|
|
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
|
|
|
|
Множественный R |
0,987444 |
|
|
|
|
|
|
|
R-квадрат |
0,975045 |
|
|
|
|
|
|
|
Нормированный R-квадрат |
0,97396 |
|
|
|
|
|
|
|
Стандартная ошибка |
2,120415 |
|
|
|
|
|
|
|
Наблюдения |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
Регрессия |
1 |
4040,588 |
4040,588 |
898,6755 |
6,15E-20 |
|
|
|
Остаток |
23 |
103,4117 |
4,49616 |
|
|
|
|
|
Итого |
24 |
4144 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
Y-пересечение |
10,19955 |
4,065172 |
2,509008 |
0,019601 |
1,790101 |
18,609 |
1,790101 |
18,609 |
x |
0,955538 |
0,031875 |
29,97792 |
6,15E-20 |
0,8896 |
1,021476 |
0,8896 |
1,021476 |
Полученное значение коэффициента регрессии b=0,955538 показывает, что при увеличении фактора х на 1 единицу от своего среднего уровня, показательный признак у увеличится на 0,955538 единиц от своего среднего уровня.
Найдем
коэффициент аппроксимации:A=
![]()
А=1/25*0,2729*100=1,091599
Полученное значение аппроксимации А=1,091599 меньше допустимого значения. Это означает, что линейную модель можно считать адекватной.
Найдем
коэффициент критерия Фишера: F=
![]()
F=(0,975045/(1-0,975045))*23=898,6755
Полученное значение F критерия Фишера F=898,6755 больше чем табличное значение (F=4,24), так что модель можно считать статистически значимой.
Найдем
коэффициент эластичности: Э=![]()
Э=0,955538*126,84/131,4=0,922378
Полученное значение коэффициента эластичности Э=0,922378 показывает, что при увеличении фактора х на 1% от своего среднего уровня, результативный показатель у увеличится на 0,922378 от своего среднего уровня.
Найдем
значение коэффициента корреляции: r=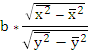
r=![]() =0,987444
=0,987444
Полученное значение коэффициента корреляции r=0,987444 показывает, что связь между переменными х и у тесная.
