3.3. Формулы расчета пружин растяжения

Основные понятия

Пружина растяжения — это спирально-цилиндрическая пружина, витки которой прилегают друг к другу. Пружина подвергается действию противоположно направленных усилий, приложенных вдоль ее оси.

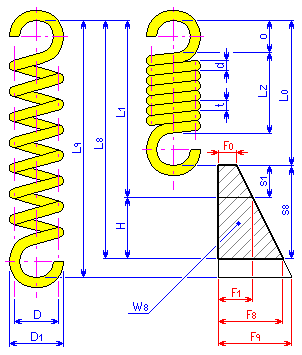
Размеры

d	диаметр проволоки [мм, д]
D	средний диаметр пружины [мм, д]
D1	наружный диаметр пружины [мм, д]
D2	внутренний диаметр пружины [мм, д]
H	рабочая деформация [мм, д]
t	шаг активных витков в ненагруженном состоянии [мм, д]
o	высота ушка [мм, д]
sx	деформация пружины [мм, д]
Lx	длина пружины [мм, д]
Fx	рабочая сила, действующая на пружину [Н, фунт]
W8	энергия деформации [Дж, фут фунт]
x	индекс, обозначающий состояние пружины

Навивка

1. Вправо (стандарт)

2. Влево (должна отображаться соответствующая надпись)

Состояния

1. Свободное: пружина не нагружена (индекс 0)

2. Предварительная нагрузка: пружина с минимальной рабочей нагрузкой (индекс 1)

3. Полная нагрузка: пружина с максимальной рабочей нагрузкой (индекс 8)

4. Предел: пружина вдавлена до касания витков (индекс 9).

Зацепы пружин растяжения

Высота зацепа пружины растяжения

Где:

L0	длина пружины в свободном состоянии [мм]
LZ	длина части пружины с витками [мм]

Часто используемые зацепы пружин растяжения

Тип зацепа и информация о размерах	Изображение
Половина витка, o = 0,55...0,8 D2
Обычно d ≤ 6,3 мм, D >= 3,15 мм, i >= 9
Полный виток, o = 0,8...1,1 D2
Используется без ограничений
Полный виток сбоку, o  D2
Когда нагрузка не обязательно должна прикладываться по оси
Полный виток внутри, o = 1,05...1,2 D2
Обычно d  ≥ 10 мм, i >= 7
Поднятый зацеп, o = 1,2 D2 ... 30 d
Обычно для d = от 0,5мм до 4 мм, o ≤ 100 мм
Два полных витка, o D
Используется без ограничений
Два полных витка сбоку, o  D2
Когда нагрузка не обязательно должна прикладываться по оси

Расчет пружин в метрических единицах

Общие формулы расчета

Коэффициент использования материала

Наружный диаметр пружины

D₁ = D + d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Внутренний диаметр пружины

D₂ = D - d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Рабочая деформация

H = L₈1_{= s}8₁[мм]

Где:

	L8	длина полностью нагруженной пружины [мм]
	L1	длина предварительно нагруженной пружины [мм]
	s8	деформация полностью нагруженной пружины [мм]
	s1	деформация предварительно нагруженной пружины [мм]

Высота зацепа пружины

Где:

	L0	длина пружины в свободном состоянии [мм]
	LZ	длина части пружины с витками [мм]

Индекс пружины

c = D/d [-]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Поправочный коэффициент Валя

Где:

	c	индекс пружины [-]
	LZ	длина части пружины с витками [мм]

Начальное растяжение

Где:

	d	диаметр проволоки [мм]
	0	напряжение в свободном состоянии [Мпа]
	D	средний диаметр пружины [мм]
	Kw	поправочный коэффициент Валя [-]

Общая сила, действующая в пружине

Где:

	d	диаметр проволоки [мм]
	G	напряжение при кручении – это усилие на единицу площади материала пружины при изгибе [фн/кв. материала пружины в общем случае [МПа]
	D	средний диаметр пружины [мм]
	Kw	поправочный коэффициент Валя [-]
	G	модуль упругости материала пружины [МПа]

Жесткость пружины

Где:

	d	диаметр проволоки [мм]
	G	модуль упругости материала пружины [МПа]
	D	средний диаметр пружины [мм]
	n	количество активных витков [-]
	F8	рабочее усилие в полностью нагруженной пружине [МПа]
	F1	рабочее усилие в минимально нагруженной пружине [МПа]
	H	рабочая деформация [мм]

Расчет конструкции пружины

При проектировании пружины подбирается диаметр проволоки, количество витков и длина свободной пружины L₀ для заданной нагрузки, материала и сборочных размеров.

Если рассчитанная пружина не соответствует ни одному значению диаметра проволоки для данного напряжения ₀ согласно формуле, расчет пружины повторяется с использованием скорректированного значения напряжения в свободном состоянии из рекомендуемого диапазона.

Пружине без начального растяжения соответствует средний рекомендуемый шаг витков t = 0,35 D [мм].

Если рассчитанная пружина не соответствует ни одному значению диаметра проволоки для выбранного шага, расчет пружины повторяется с использованием скорректированного значения шага из рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4 D [мм].

Конструкция пружины определяется с учетом условия прочности ₈≤ u_s_A и рекомендуемых диапазонов некоторых геометрических параметров пружины: L₀≤ D и L₀≤ 31,5 д и 4 ≤ D/d ≤16 и n  2.

Задание нагрузки, материала и сборочных размеров пружины

Вначале выполняется проверка входных величин для расчета.

Затем вычисляется длина пружины в свободном состоянии.

После расчета выбирается диаметр проволоки, количество витков и диаметры пружины – так, чтобы высота зацепа соответствовала выбранному типу зацепа. Кроме того, должны выполняться упомянутые выше прочностные и геометрические условия. Конструкция пружины должна удовлетворять по диаметрам всем заданным начальным условиям. При отсутствии таких дополнительных условий предельный диаметр пружины устанавливается по геометрическим условиям для минимально/максимально допустимого диаметра проволоки.

Отбираются все диаметры проволоки (от меньшего к большему), которые проходят по прочностным и геометрическим условиям. Проверяются высота зацепа и количество витков. Если все условия выполнены, расчет конструкции завершается, и текущие значения параметров принимаются в качестве его результатов, независимо от того, как прошел бы расчет при других подходящих диаметрах проволоки. Таким образом, полученная пружина имеет минимально возможный диаметр проволоки и минимально возможное количество витков.

Вычисленное значение высоты зацепа должно находиться в пределах d ≤ o ≤ 30 d. Комбинация диаметра проволоки, количества витков и диаметра пружины должна давать в итоге такую высоту зацепа, которая удовлетворяет его типу. Вначале в качестве типа зацепа берется полный виток, затем, если он не годится–полный виток внутри и т.д.

Задание нагрузки, материала и диаметра пружины

Вначале выполняется проверка входных величин для расчета.

После проверки выбирается диаметр проволоки, количество витков, длина пружины в свободном состоянии и сборочные размеры пружины – так, чтобы высота зацепа соответствовала выбранному типу зацепа. Кроме того, должны выполняться прочностные и геометрические условия. Если сборочный размер L₁ или L₈ взят из спецификации или значение рабочей деформации пружины ограничено, конструкция пружины должна соответствовать этому условию. В остальных случаях предельные значения сборочных размеров пружины и ее длины в свободном состоянии определяются геометрическими условиями для заданного диаметра пружины и минимального/максимального допустимого диаметра проволоки.

Формула для проектирования пружины по заданному диаметру проволоки.

где значение ₈ = 0,85 _A используется в качестве величины напряжения материала пружины при кручении в полностью нагруженном состоянии.

Если для данного диаметра проволоки не удается подобрать подходящую комбинацию размеров пружины, расчетная процедура оценивает другие диаметры проволоки. Они проверяются, начиная от меньшего к большему, до тех пор пока не будет достигнуто такое количество витков, при котором высота зацепа удовлетворяет всем условиям. Расчет конструкции завершается, и текущие значения параметров принимаются в качестве его результатов, независимо от того, как прошел бы расчет при других подходящих диаметрах проволоки. Таким образом, полученная пружина имеет минимально возможный диаметр проволоки и минимально возможное количество витков.

Вычисленное значение высоты зацепа должно находиться в пределах d ≤ o ≤ 30 d. Для высоты, вычисленной таким способом, выбирается соответствующий тип зацепа. Комбинация диаметра проволоки, количества витков, длины пружины в свободном состоянии и сборочных размеров пружины должна давать в итоге такую высоту зацепа, которая удовлетворяет его типу. Вначале в качестве типа зацепа берется полный виток, затем, если он не годится–полный виток внутри и т.д.

Задание максимального рабочего усилия, материала, сборочных размеров и диаметра пружины

Вначале выполняется проверка входных величин для расчета.

Затем подбирается диаметр проволоки, количество витков, длина свободной пружины и минимальное рабочее усилие F₁ таким образом, чтобы высота зацепа пружины соответствовала выбранному типу зацепа. Кроме того, должны выполняться прочностные и геометрические условия.

Формула для проектирования пружины по заданному диаметру проволоки.

где значение ₈ = 0,9 _A используется в качестве величины напряжения материала пружины при кручении в полностью нагруженном состоянии.

Если для данного диаметра проволоки не удается подобрать подходящую комбинацию размеров пружины, расчетная процедура оценивает другие диаметры проволоки. Они проверяются, начиная от меньшего к большему, до тех пор пока не будет достигнуто такое количество витков, при котором высота зацепа удовлетворяет всем условиям. Расчет конструкции завершается, и текущие значения параметров принимаются в качестве его результатов, независимо от того, как прошел бы расчет при других подходящих диаметрах проволоки. Таким образом, полученная пружина имеет минимально возможный диаметр проволоки и минимально возможное количество витков.

Проверочный расчет пружины

Расчет соответствующих значений сборочных размеров и рабочего отклонения для указанной нагрузки, материала и размеров пружины.

Сначала проверяются расчетные входные значения. Затем на основании приведенных ниже формул вычисляются сборочные размеры.

Длина предварительно нагруженной пружины

Длина полностью нагруженной пружины

Где:

	L0	длина пружины в свободном состоянии [мм]
	F1	рабочая сила в минимально нагруженной пружине [мм]
	D	средний диаметр пружины [мм]
	n	количество активных витков [-]
	G	модуль упругости материала пружины [МПа]
	d	диаметр проволоки [мм]
	F8	рабочее усилие в полностью нагруженной пружине [МПа]

Рабочая деформация

H = L₁8_[мм]

Расчет рабочих сил

Расчет соответствующих сил, действующих в пружинах в рабочем состоянии для указанного материала, сборочных размеров и размеров пружины. Сначала проверяются и рассчитываются входные данные, а затем выполняется расчет рабочих сил с помощью следующих формул.

Минимальное рабочее усилие

Максимальное рабочее усилие

Расчет выходных параметров пружины

Эта часть является общей для всех типов расчета пружины. Расчет производится в следующем порядке.

Коэффициент высоты зацепа

Жесткость пружины

Длина части с витками

Пружина без начального растяжения
	Lz = t n + d [мм]
Пружина с начальным растяжением
	Lz = 1,03 (n + 1) d [мм]

Деформация предварительно нагруженной пружины

s₁ = L₁ - L₀ [мм]

Полная деформация пружины

s₈ = L₈ - L₀ [мм]

Напряжение при кручении материала пружины в состоянии предварительной нагрузки

Напряжение материала пружины при кручении при полном нагружении

Предельное усилие в пружине

Деформация в предельном состоянии

Где:

	k	жесткость пружины [Н/мм]
	F9	рабочее усилие в пружине, нагруженной до предела [Н]
	F0	начальное растяжение пружины [Н]

Предельная длина пружины

L₉ = L₀ + s₉ [мм]

Энергия деформации пружины

Длина развернутой проволоки

l = 3.2 D n + l0 [мм]
	Где длина развернутого зацепа l0:
		для половины витка
			l0 =  D + 4 o - 2 D - 2 d [мм]
		для полного витка
			l0 = 2 ( D - 2 d) [мм]
		для полного витка сбоку
			l0 = 2 ( D - 2 d) [мм]
		для полного витка внутри
			l0 = 2 ( D - d) [мм]
		для поднятого зацепа
			l0 =  D + 2 o - D + 3 d [мм]
		для двух полных витков
			l0 = 4  D [мм]
		для двух полных витков сбоку
			l0 = 4  D [мм]
		для неуказанного типа зацепа
			l0 = 0 [мм]

Масса пружины

Собственная частота колебаний пружины

Проверка нагрузки пружины

 ₈≤ u_s _A

Обзор используемых переменных:

d	диаметр проволоки [мм]
k	жесткость пружины [Н/мм]
D	средний диаметр пружины [мм]
D1	наружный диаметр пружины [мм]
D2	внутренний диаметр пружины [мм]
F	обобщенное усилие, приходящееся на пружину [Н]
G	модуль упругости материала пружины при сдвиге [МПа]
H	рабочая деформация [мм]
c	индекс пружины [-]
Kw	поправочный коэффициент Валя [-]
l	длина развернутой проволоки [мм]
L	обобщенная длина пружины [мм]
LZ	длина части пружины с витками [мм]
m	масса пружины [N]
n	количество активных витков [-]
o	высота зацепа пружины [мм]
t	шаг активных витков в ненагруженном состоянии [мм]
s	обобщенная деформация (растяжение) пружины [мм]
us	коэффициент использования материала
	плотность материала пружины [Н/мм3]
	напряжение при кручении – это усилие на единицу площади материала пружины при изгибе [фн/кв. материала пружины в общем случае [МПа]
 A	допустимое напряжение материала пружины при кручении [МПа]