Экспериментальное подтверждение молекулярно-кинетической теории

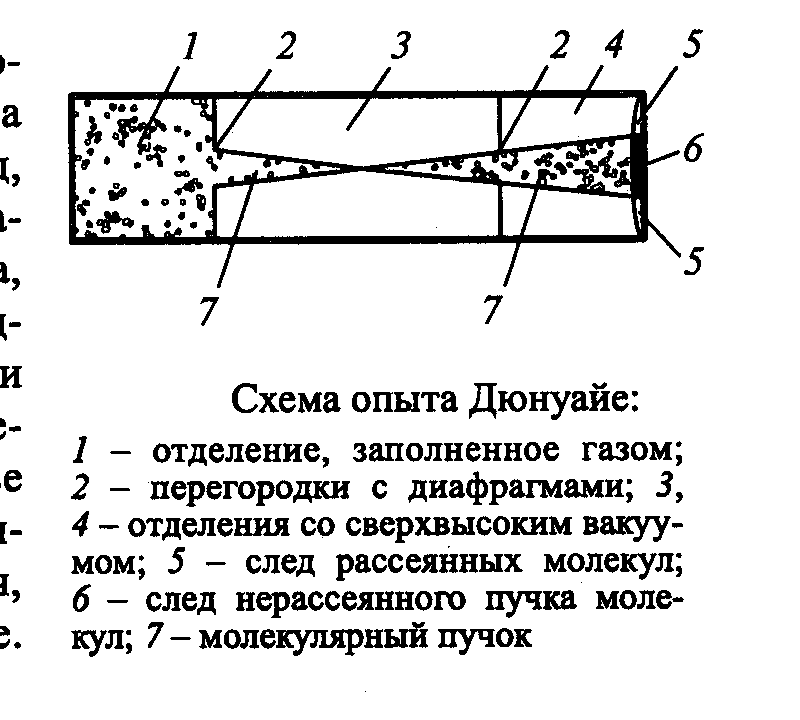
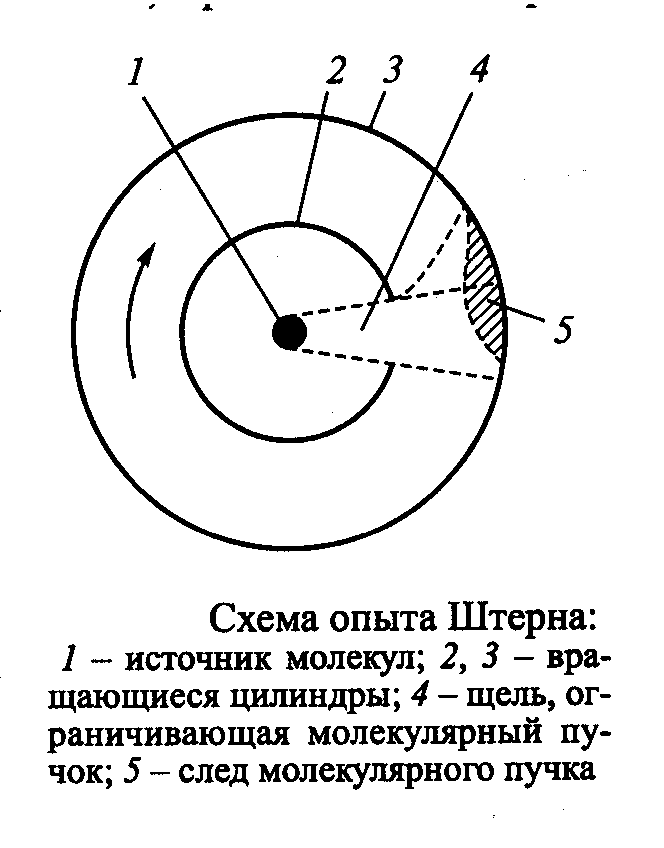
Лекция 12 Теплоёмкость идеального газа

Теплоёмкостью макросистемы (тела или некоторого количества газа) называют количество тепла, которое нужно сообщить макросистеме, чтобы повысить её температуру на один кельвин:

.

Молярной теплоёмкостью называют количество тепла, которое необходимо сообщить одному молю вещества, чтобы повысить его температуру на один кельвин:

, Дж/моль^.К.

В справочных таблицах обычно указывают удельную теплоёмкость с, Дж/кг^.К

с = С/М , где

М – молярная масса.

Теплоёмкость также как и зависит от процесса и является функцией процесса.

Для анализа различных процессов в газах удобно пользоваться молярной теплоёмкостью. Особое значение имеют молярные теплоёмкости для двух процессов: при постоянном объёме С_V и при постоянном давлении С_р .

При постоянном объёме dV = 0. Следовательно δА = р^.dV = 0 и имеем

.

Так как теплоёмкость в широком интервале температур практически не меняется, то получаем

.

Ранее было показано, что , поэтому можно считать, что для идеального газа

Молярная теплоёмкость произвольного процессa

.

Если процесс изобарический (p = const), то из уравнения состояния следует, что р(dV/dT) = ν^.R , и соответствующая молярная теплоёмкость

(соотношение Майера).

Важной характеристикой газов является отношение , которое обозначают буквой γ и называют постоянной адиабаты.

.

Для изменения внутренней энергии ν молей идеального газа получаем: .

Адиабатический процесс

Адиабатическим называют процесс, который проходит без теплообмена с окружающей средой. Для идеального газа получаем:

,

,

,

.

После интегрирования получаем уравнение адиабаты в переменных р , V или уравнение Пуассона:

В переменных Т, V для уравнения адиабаты получаем (используя p^.V = ν^.R^.T):

.

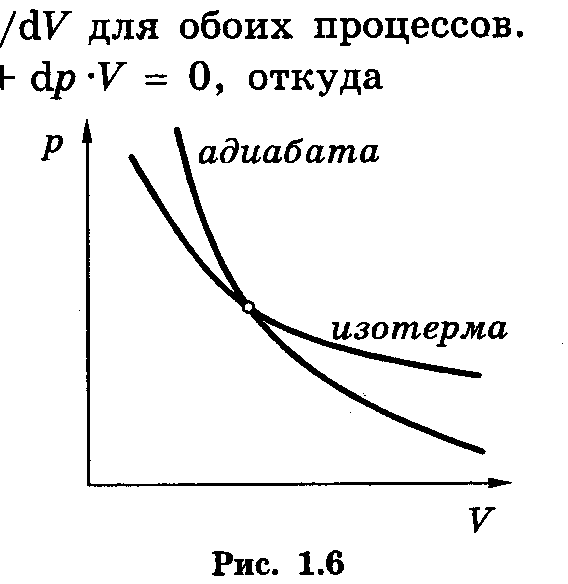
Адиабата в координатах р , V идёт круче изотермы (рV = const)

Политропический процесс

Политропическими называют процессы, уравнение которых в переменных р , V имеет вид

, где

п – произвольное число, как положительное, так и отрицательное, а также равное нулю.

Например, политропическими являются изохорический (V = const, п ), изобарический (р = const, п = 0), изотермический (рV = const, п = 1) и адиабатический (п = γ) процессы.

Теплоёмкость всех политропических процессов остаётся постоянной:

.

Для получения выражения для С_п воспользуемся уравнением политропы в переменных Т, V:

.

Продифференцируем это уравнение:

или

.

Подставляя это выражение в формулу для теплоёмкости , получаем:

.

.

Используя формулу , получаем ещё одно выражение:

.

Видно, что если п = γ, то С_п = 0 как и должно быть из определения адиабатического процесса. При п = 1 получаем С_п , как и должно быть при изотермическом процессе.