Явления на границе раздела газа, жидкости и твёрдого тела

Поверхность жидкости под действием сил поверхностного натяжения стремится принять такую форму, чтобы иметь минимальную площадь.

, где

– поверхностное натяжение ( коэффициент поверхностного натяжения) Н/м;

– длина границы свободной поверхности жидкости (поверхности жидкости, граничащей с газовой фазой).

Поверхностное натяжение представляет собой силу, действующую на единицу длины контура, ограничивающего участок поверхности раздела, и направленную касательно к поверхности по внутренней нормали к контуру.

Элементарная работа, совершаемая силами поверхностного натяжения

, где

– изменение площади свободной поверхности жидкости.

Видно, что поверхностное натяжение численно равно работе, которую необходимо затратить при обратимом изотермическом процессе для увеличения площади поверхности жидкости на единицу. Указанная работа затрачивается на приращение свободной поверхностной энергии жидкости.

Поверхностное натяжение численно равно удельной (приходящейся на единицу площади) свободной поверхностной энергии:

Дж/м².

В природе силы действуют так, чтобы привести систему в состояние с наименьшей потенциальной энергией. Поэтому поверхность раздела сред стремиться уменьшится. Например, капля жидкости в свободном состоянии принимает шарообразную форму.

Если граничат друг с другом сразу три фазы: твёрдая, жидкая и газообразная, то вся система принимает конфигурацию, соответствующую минимуму суммарной энергии.

П лоскость, касательная к поверхности жидкости у её края, образует с поверхностью твёрдого тела некоторый угол , называемый краевым углом. Этот угол зависит только от поверхностных натяжений на границах раздела соприкасающихся сред.

, где

– поверхностное натяжение на границе раздела твёрдой и газовой фаз;

– поверхностное натяжение на границе раздела жидкости и газа;

– поверхностное натяжение на границе раздела твёрдой и жидкой фаз.

Если (притяжение между молекулами твёрдого тела больше, чем между молекулами жидкости), то краевой угол острый ( ). Это случай смачивания твёрдой поверхности жидкостью. Жидкость в сосуде имеет вогнутый мениск (вода в стеклянном сосуде). Полному смачиванию соответствует угол .

Если то угол тупой ( ).Это случай несмачивания твёрдой стенки жидкостью. Жидкость в сосуде имеет выпуклый мениск (ртуть в стеклянном сосуде).

К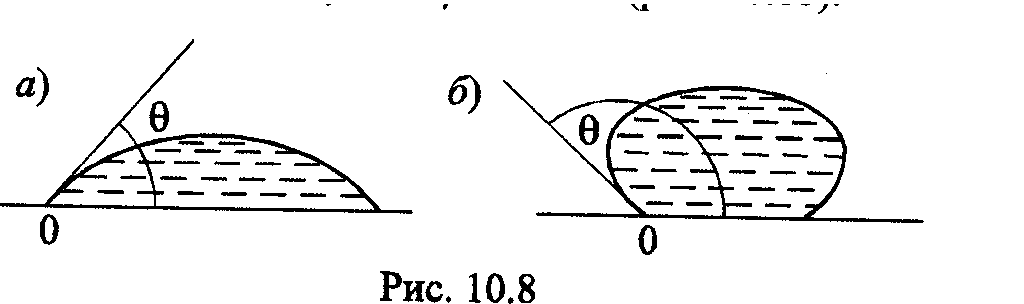 апли жидкости на горизонтальной поверхности также имеют различную форму.

Явление смачивания (или несмачивания) твёрдого тела жидкостью приводит к появлению капиллярного эффекта.

Капилляром называют тонкую трубку, вставленную в сосуд с жидкостью. Если жидкость смачивает стенки капилляра, то давление внутри жидкости уменьшается по сравнению с внешним и она поднимается внутри капилляра. Если жидкость не смачивает стенки капилляра, то уровень жидкости понижается.

Высота подъёма жидкости в капилляре определяется выражением

.

Дополнительное давление , создаваемое повер-хностью жидкости определяют по формуле Лапласа для поверхностного натяжения

, где

– радиус сферической поверхности жидкости.