Приближенное решение уравнений постановка задачи

Задача решения уравнения чаще всего встречается при изучении общетехнических и специальных дисциплин, в инженерной практике. Отыскать точное значение корня уравнения возможно лишь в некоторых редких частных случаях, причем даже в этих случаях формулы нахождения корней бывают настолько громоздкими, что ими затруднительно пользоваться. Кроме того, часто константы, входящие в уравнение, известны приближенно. Поэтому при решении уравнений широко используются методы, позволяющие получить приближенное решение с любой заданной точностью.

Пусть задано уравнение

,

где функция определена и непрерывна на некотором отрезке и имеет в нем непрерывные первую и вторую производные. Корни заданного уравнения являются нулями функции и геометрически представляют собой точки пересечения ее графика с осью  .

Рассмотрим задачу отыскания приближенных значений действительных корней заданного уравнения с любой заданной точностью. Решение задачи состоит из двух этапов.

1. Отделение корня, т. е. отыскание отрезка 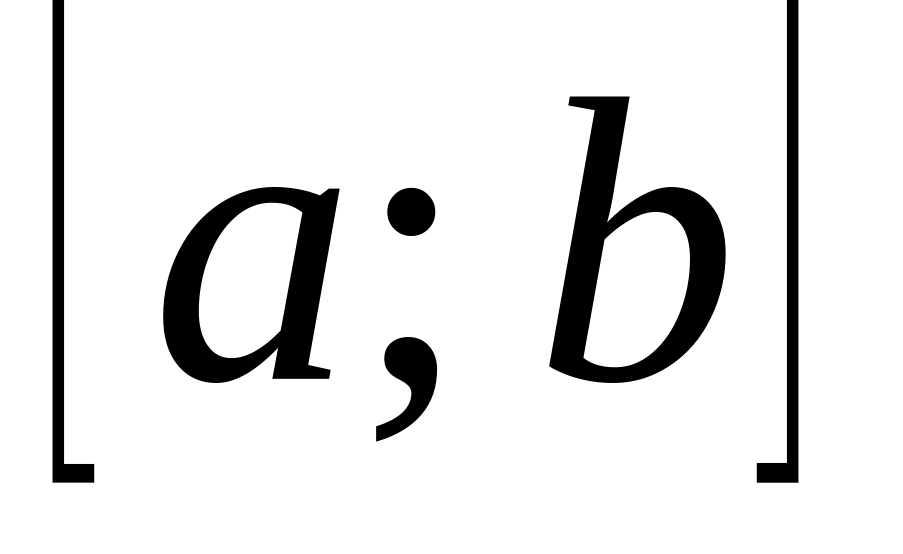, принадлежащего области определения функции , на котором находится один и только один корень уравнения .

2. Уточнение значения корня с заданной точностью.

Отделение корня уравнения Условия отделения корня

Первое условие основано на поведении функции в окрестности корня, которое выражается в том, что на концах отрезка функция имеет значения разных знаков, т. е.

.

Очевидно, что при этом внутри отрезка имеется, по крайней мере, один корень уравнения . Геометрически это означает, что график функции в точках и находится по разные стороны от оси и, следовательно, внутри отрезка обязательно должен пересекать ось . Однако это условие не гарантирует существования единственного корня.

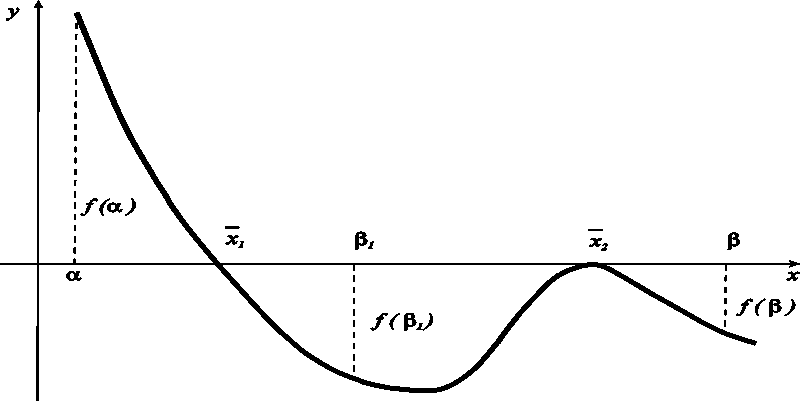
Так, например, на рисунке график функции проходит таким образом, что , , то есть , а внутри отрезка находятся два различных корня.

Заметим, что если на концах отрезка значения функции имеют один и тот же знак, то это вовсе не означает, что корень отсутствует. Например, отрезок содержит корень, но и , а значит . Точка в данном случае является кратным корнем уравнения . В дальнейшем такие корни рассматривать не будем.

Для существования единственного корня на отрезке должно выполняться еще одно условие. На отрезке функция монотонна, т. е. ее производная не меняет знак на .

Оба условия являются достаточными для существования единственного корня уравнения .

Из рисунка видно, что обоим условиям удовлетворяет отрезок , а на отрезке функция не является монотонной.

Задача отделения корня уравнения состоит в нахождении отрезка области определения функции , на котором выполнены следующие три условия:

1. ;

2. не меняет знак для ;

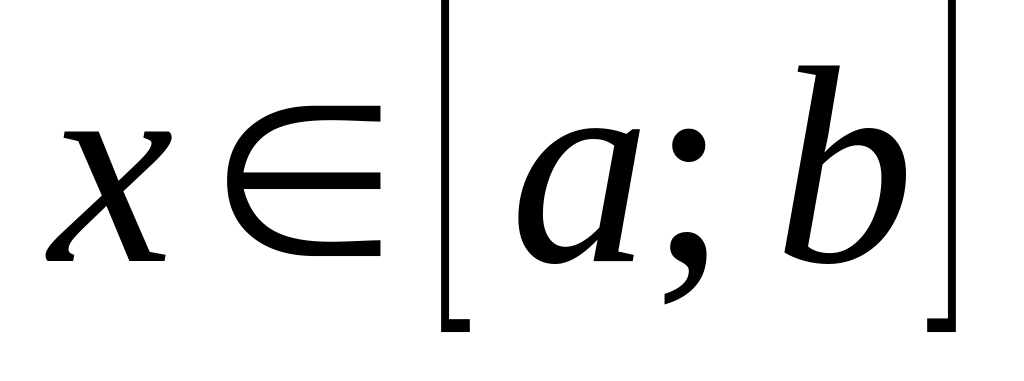3. не меняет знак для .

Третье условие означает, что график функции либо только выпуклый, либо только вогнутый на отрезке .

Отрезок при выполнении условий 1)–3) для функции называют отрезком, отделяющим корень данной функции.

Рассмотрим все возможные варианты расположения графика функции на отрезке , если выполняются условия 1)–3). При этом для производная на рисунках а) и г), и на рисунках б) и в). Вторая же производная на рисунках а) и б) и на рисунках в) и г) для всех .

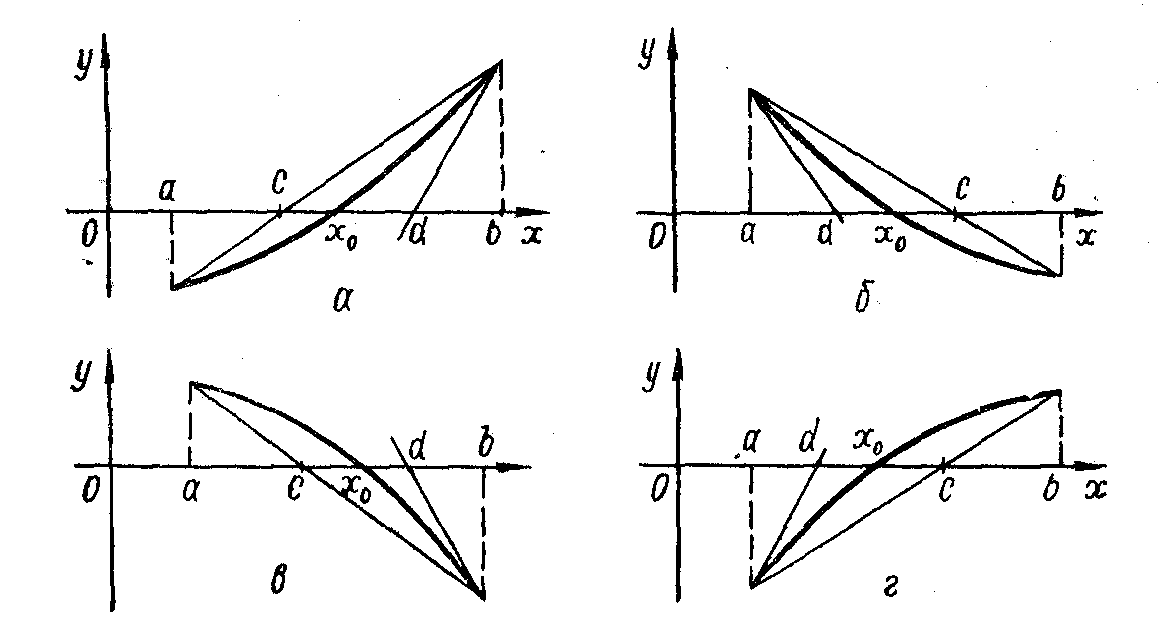
Отделение корня можно производить как аналитически, так и графически.