
- •Билет №1
- •1. Базовые конструкции языка программирования Pascal.
- •2. Предмет мпи, его цели и задачи.
- •Билет №2
- •1. Информационная технология. Этапы развития и перспективы информационных технологий.
- •2. Охарактеризовать информатику, как науку.
- •3. Задан некоторый набор товаров. Определить для каждого из товаров, какие из них имеются в каждом магазине и каких товаров нет ни в одном магазине.
- •Билет №3
- •1. Алгебра высказываний как модель алгебры Буля, ее аксиоматическое задание. Принцип двойственности и теорема двойственности.
- •3. Операция следования или импликации ( → )
- •4. Операция эквивалентности ( ↔ )
- •2. Цели пропедевтического курса информатики
- •3. Дан целочисленный массив с количеством элементов n. Напечатать те его элементы, индексы которых являются степенями двойки (1,2,4,8,…). Задачу решить с использованием процедуры или функции.
- •Билет №4
- •1. Метод простой итерации при решении уравнения с одной переменной.
- •2. Цели школьной информатики. Компьютерная грамотность, алгоритмическая и информационная культура.
- •3. В заданном одномерном массиве поменять местами соседние элементы, стоящие на четных местах, с элементами, стоящими на нечетных местах.
- •Билет №5
- •2. Классическое понятие урока, основные цели.
- •3. Задано некоторое множество м и множество т того же типа. Подсчитать количество элементов в т и м, которые не совпадают.
- •Билет №6
- •1. Основные комбинаторные объекты и числа.
- •2. Типы уроков информатики.
- •3. Дана посл-ть действительных чисел а1,а2,…,аn. Заменить все её члены, большие данного z, этим числом. Подсчитать количество замен.
- •Билет №7
- •1.Архитектура эвм
- •2. Внеурочная работа по информатике.
- •3. Определить те имена учеников, которые встречаются во всех классах данной параллели.
- •Билет №8
- •1. Понятие о компьютерных сетях. Типы сетей. Топология. Классификация.
- •2. Функции контроля знаний учащихся.
- •3. Решите задачу линейного программирования симплексным методом. При решении задачи покажите умения отыскания исходного базиса с помощью введения искусственного базиса:
- •Билет №9
- •1. Основные понятия теории кодирования. Оптимальный код Шеннона-Фано.
- •2. Виды контроля знаний
- •3. Распечатать список учеников, фамилии которых начинаются на букву в, с указанием даты их рождения.
- •Билет №10
- •1. Теория множеств: множества и операции над множествами, основные проблемы.
- •2. Схема анализа урока
- •3. Дана строка, содержащая английский текст; слова разделены пробелами. Найти количество слов, начинающихся с буквы b.
- •Билет №11
- •2. Примерная памятка для самоанализа урока учителем
- •Билет №12
- •1. Условный экстремум: функция Лагранжа, метод множителей Лагранжа.
- •2. Классификация педагогических программных средств.
- •3. Решите задачу линейного программирования графическим методом.
- •Билет №13
- •2. Дидактические требования к современному року
- •3. Составить программу, определяющую, в каком из данных двух чисел больше цифр. Задачу решить с использованием процедуры или функции.
- •Билет №14
- •Билет №15
- •1. Основы теории распознавания образов(ро).
- •2. Психологические требования
- •Билет №16
- •1. Рекуррентные соотношения.
- •2. Предмет мпи, его цели и задачи.
- •Билет №17
- •3. Даны целые положительные числа а1,а2,…,аn. Найти среди них те, которые являются квадратами числа m.
- •Билет №18
- •1. Информационная емкость. Формула информационной емкости.
- •2. Виды контроля знаний
- •3. Дана строка. Указать те слова, которые содержат хотя бы одну букву к. Задачу решить с использованием процедуры или функции.
- •Билет №19
- •1. Метод простой итерации для слау
- •2. Понятие алгоритма.
- •Базовые алгоритмические структуры
- •3. Решите задачу линейного программирования графическим методом.
- •Билет №20
- •1. Описание процедур и функции языка программирования Pascal.
- •Описание и вызов процедур и функций
- •2. Свойства алгоритмов. Формы представления алгоритмов.
- •3. Дана строка; слова разделены пробелами. Подсчитать, сколько в ней букв r, k, t.
- •Билет №21
- •2. Классификация педагогических программных средств.
- •3. Дана строка; слова разделены пробелами. Подсчитать, сколько слов в строке.
- •Билет №22
- •2. Система методов преподавания информатики в школе. (Группы, методы)
- •3. Дана последовательность действительных чисел а1,а2,…,аn. Указать те элементы, которые принадлежат отрезку [c,d].
- •Билет №23
- •2. Объяснительно-иллюстративный метод и репродуктивный метод
- •3. Составить программу для вычисления суммы факториалов, всех чисел, кратных 3, от а до в. Задачу решить с использованием процедуры или функции.
- •Билет №24
- •1. Методы численного интегрирования дифференциальных уравнений.
- •2.Проблемный метод, частично-поисковый и эвристический метод
- •3. Заполнить таблицу размерности n*n:
- •Билет №25
- •1. Основные типы данных Pascal.
- •2. Типы уроков информатики.
- •Билет №26
- •1. Перспективы развития информационной технологии.
- •2. Информатика как школьная дисциплина.
- •Билет №27
- •1. Средства программирования в Delphi. Работа в Delphi
- •2. Классическое понятие урока, основные цели.
- •3. Дано простое число р. Найти и вывести на экран следующее за ним простое число. Задачу решить с использованием процедуры или функции.
- •Билет №28
- •1. Двойственность в линейном программировании
- •2. Схема анализа урока
- •3. Дан файл, содержащий различные даты. Каждая дата – это число, месяц и год. Найти самую позднюю дату.
- •Билет №29
- •2. Понятие алгоритма.
- •Базовые алгоритмические структуры
- •3. Заполнить таблицу размерности n*n:
- •Билет №30
- •2. Свойства алгоритмов. Формы представления алгоритмов.
- •3. Дано натуральное число п. Вычислить:
- •Билет №31
- •1. Интерполяционный многочлен Лагранжа и оценка его погрешности
- •2. Внеурочная работа по информатике.
- •3. Дана строка символов, среди которых есть одна открывающаяся и одна закрывающаяся скобка. Вывести на экран все символы, расположенные внутри этих скобок.
- •Билет №32
- •1.Система счисления с произвольным основанием.Перевод из одной с.С в другую.Операции над числами в с.С с произвольным основанием.
- •2. Функции контроля знаний учащихся.
- •3. Составить программу, которая запрашивает пароль (например, четырёхзначное число) до тех пор, пока он не будет правильно введён.
- •Билет №33
- •1.Технология «КлиентСервер». Одноранговые и распределительные системы.
- •2. Дидактические требования к современному року
- •3. Заполнить таблицу размерности n*n:
- •Билет №34
- •1.Разработка мультимедийных приложений в среде Delphi.
- •2. Примерная памятка для самоанализа урока учителем
- •3. Из данного списка спортсменов распечатать сведения о тех из них, кто занимается плаванием. Указать того, кто занимается спортом дольше всех.
- •Билет №35
- •1. Проблема разрешимости (разрешения) для класса однотипных задач. Проблема разрешимости в алгебре высказываний и способы их разрешения.
- •2. Система методов преподавания информатики в школе. (Группы, методы)
- •3. Строка содержит одно слово. Проверить, будет ли оно читаться одинаково справа налево и слева направо (т.Е. Является ли оно палиндромом).
- •Билет №37
- •1. Высказывательные формы (предикаты). Способы их задания. Логические операции над предикатами.
- •2. Информатика как школьная дисциплина.
- •3. В строке имеется одна точка с запятой (;). Подсчитать количество символов до точки с запятой и после неё.
3. Дана строка; слова разделены пробелами. Подсчитать, сколько слов в строке.
program lab47;
var s:string;
i,k:integer;
begin
writeln('Vvedite stroku');
readln(s);
k:=1;
for i:=1 to length(s) do
if (s[i]=' ') and (s[i+1]<>' ') then
k:=k+1;
writeln(k);
end.
Билет №22
1. Графическое моделирование- результатов научных исследований. Общую цель научной графики можно сформулировать так: сделать невидимое и абстрактное “видимым”. Последнее слово заключено в кавычки, т.к. эта видимость часто весьма условна. Трёхмерная графика (3D Graphics, Три измерения изображения, 3 Dimensions, русск. 3 измерения) — раздел компьютерной графики, совокупность приемов и инструментов (как программных, так и аппаратных), предназначенных для изображения объёмных объектов. Больше всего применяется для создания изображений на плоскости экрана или листа печатной продукции в архитектурной визуализации, кинематографе, телевидении, компьютерных играх, печатной продукции, а также в науке и промышленности. Трёхмерное изображение на плоскости отличается от двумерного тем, что включает построение геометрической проекции трёхмерной модели сцены на плоскость (например, экран компьютера) с помощью специализированных программ. При этом модель может, как соответствовать объектам из реального мира (автомобили, здания, ураган, астероид), так и быть полностью абстрактной (проекция четырёхмерного фрактала). Для получения трёхмерного изображения на плоскости требуются следующие шаги: моделирование — создание трёхмерной математической модели сцены и объектов в ней. визуализация — построение проекции в соответствии с выбранной физической моделью.вывод полученного изображения на устройство вывода — дисплей или принтер. Однако, в связи с попытками создания 3D-дисплеев и 3D-принтеров, трёхмерная графика не обязательно включает в себя проецирование на плоскость.
Преобразование
координат.
Преобразование декартовых координат
при параллельном сдвиге осей определяется
формулами:
![]() ,
,
![]() .
Здесь x, y - координаты произвольной точки
М плоскости относительно старых осей,
x’, y’ - координаты той же точки относительно
новых осей, a, b - координаты нового начала
O’ относительно старых осей (говорят
также, что a - величина сдвига в направлении
оси абсцисс, b - величина сдвига в
направлении оси ординат). Преобразование
декартовых прямоугольных координат
при повороте осей на угол (который надо
понимать, как в тригонометрии) определяется
формулами:
.
Здесь x, y - координаты произвольной точки
М плоскости относительно старых осей,
x’, y’ - координаты той же точки относительно
новых осей, a, b - координаты нового начала
O’ относительно старых осей (говорят
также, что a - величина сдвига в направлении
оси абсцисс, b - величина сдвига в
направлении оси ординат). Преобразование
декартовых прямоугольных координат
при повороте осей на угол (который надо
понимать, как в тригонометрии) определяется
формулами:
![]() ,
,
![]() .
Здесь x, y суть
.
Здесь x, y суть
координаты произвольной точки М плоскости относительно старых осей, x’, y’ - координаты той же точки относительно новых осей.
Формулы:
![]() ,
,
![]() определяют преобразование координат
при параллельном сдвиге системы осей
на величину а в направлении Ох, на
величину b в направлении Оу и последующем
повороте осей на угол
определяют преобразование координат
при параллельном сдвиге системы осей
на величину а в направлении Ох, на
величину b в направлении Оу и последующем
повороте осей на угол
![]() . Все указанные формулы соответствуют
преобразованию координат при неизменном
масштабе.
. Все указанные формулы соответствуют
преобразованию координат при неизменном
масштабе.
Перенос и повороты в трех мерном пространстве. Перенос: P(x,y,z) P’(x’,y’,z’)
![]()
- перенос в трехмерном пространстве (ai = const)
[x’,y’,z’,1] = [x,y,z,1]T
, T=
![]() (3.1) Т – матрица переноса
(3.1) Т – матрица переноса
1,2,3 стр. матр. Т - отображение бесконечно удаленной точки [a1,a2,a3,1] - отображение начала координат. Поворот
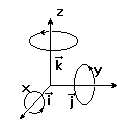
Cos a = C
Sin a = S
[x’,y’,z’] = [x,y,z]Rz .
Матрица поворота вокруг оси Oz :
Rz =
![]()
Матрица поворота вокруг оси Ox :
Rx =
![]()
Матрица поворота вокруг оси Oy :
Ry =
![]()
Матрица переноса начала координат в какую-то точку А
T-1 =
![]()
Rx-1 =
![]() (3.4)
(3.4)
Ry-1 =
![]() (3.5)
(3.5)
Rz-1 =
![]() (3.6)
(3.6)
Матрица поворота вокруг линии, проходящей через начало координат (поворот вокруг вектора v с началом в точке O)
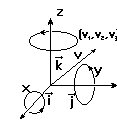
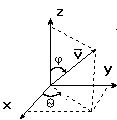
r = |v| =
![]()
q =
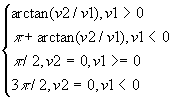
v1 = r Sin j Cos q
v2 = r Sin j Sin q
v3 = r Cos j
[x’,y’,z’] = [z,y,z] Rz-1 - совпадает с положительным направлением оси Oz
Ось x’ имеет положительное направление вектора (v1,v2,0)
[x’’,y’’,z’’] = [z’,y’,z’] Ry-1
[x’’’,y’’’,z’’’] = [z’’,y’’,z’’] Rv-1
Rv =
[x’’’,y’’’,z’’’] = [x,y,z] Rz-1 Ry-1 Rx-1
[x*,y*,z*] = [x’’’,y’’’,z’’’] Ry Rz - возвращение назад координатной оси
