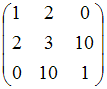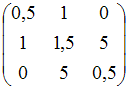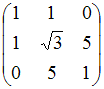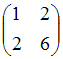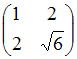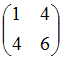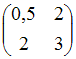Квадратичные формы

Тема: Квадратичные формы

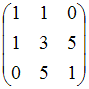
Матрице 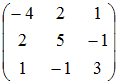 соответствует квадратичная форма , равная …

Решение: Слагаемые из формы можно представить в виде . Они соответствуют как i-строке и j-столбцу, так и j-строке и i-столбцу матрицы в силу того, что , поэтому на каждой из двух позиций ij и ji матрицы записывается по . Соответственно, коэффициенты формы при квадратах неизвестных, то есть , записываются на главной диагонали. Для данной формы элементы матрицы равны: Следовательно, данная квадратичная форма имеет вид:

Тема: Квадратичные формы

Матрица квадратичной формы  имеет вид …

Решение: Матрица квадратичной формы симметрична относительно главной диагонали. Слагаемые из формы можно представить в виде . Они соответствуют как i-строке и j-столбцу, так и j-строке и i-столбцу матрицы в силу того, что , поэтому на каждой из двух позиций ij и ji матрицы записывается по . Соответственно коэффициенты формы при квадратах неизвестных, т.е.   , записываются на главной диагонали. Для данной формы элементы матрицы   . Следовательно, заданная квадратичная форма описывается матрицей .

Тема: Квадратичные формы

Канонический вид квадратичной формы  может иметь вид…

Тема: Квадратичные формы Матрице 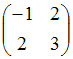  соответствует квадратичная форма  , равная …

Решение: Слагаемые из формы можно представить в виде  . Они соответствуют как i-строке и j-столбцу, так и j-строке и i-столбцу матрицы в силу того, что  , поэтому на каждой из двух позиций ij и ji матрицы записывается по  . Соответственно коэффициенты формы при квадратах неизвестных, то есть   , записываются на главной диагонали. Для данной формы элементы матрицы  . Следовательно, заданная квадратичная форма имеет вид  .

Тема: Квадратичные формы Матрица квадратичной формы   имеет вид …

Решение: Матрица квадратичной формы симметрична относительно главной диагонали. Слагаемые из формы можно представить в виде  . Они соответствуют как i-строке и j-столбцу, так и j-строке и i-столбцу матрицы в силу того, что  , поэтому на каждой из двух позиций ij и ji матрицы записывается по  . Соответственно коэффициенты формы при квадратах неизвестных, т.е.   , записываются на главной диагонали. Для данной формы элементы матрицы  . Следовательно, заданная квадратичная форма описывается матрицей  .