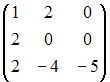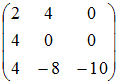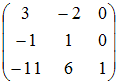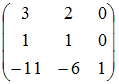Линейная алгебра Раздел: Вычисление определителей
Тема: Вычисление определителей
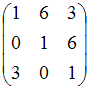
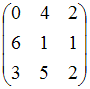
Определитель
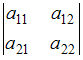 равен
…
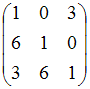
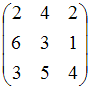
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Определитель
второго порядка вычисляется по формуле:
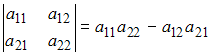 .
.

Тема: Вычисление определителей
Корень
уравнения
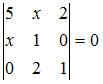 равен
…
равен
…
|
|
|
– 1 |
|
|
|
1 |
|
|
|
– 5 |
|
|
|
3 |
Решение:
Определитель
третьего порядка можно вычислить,
например, разложением по элементам
первой строки:
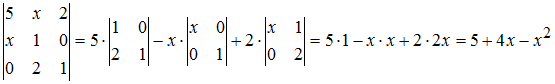 .По
условию задачи определитель должен
равняться 0, то есть
.По
условию задачи определитель должен
равняться 0, то есть
![]() .
Следовательно,
.
Следовательно,![]() .
.
Тема: Вычисление определителей
Корень уравнения равен …
|
|
|
– 1 |
|
|
|
1 |
|
|
|
– 5 |
|
|
|
3 |
Решение: Определитель третьего порядка можно вычислить, например, разложением по элементам первой строки: .По условию задачи определитель должен равняться 0, то есть . Следовательно, .
Тема:
Вычисление
определителей
Корень
уравнения 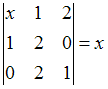 равен
…
равен
…
|
|
|
– 3 |
|
|
|
3 |
|
|
|
0 |
|
|
|
– 9 |
Решение:
Определитель
третьего порядка можно вычислить,
например, разложением по элементам
первой строки:
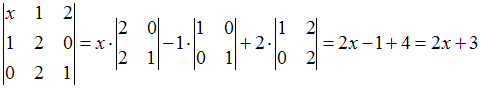 . По
условию задачи определитель должен
равняться
. По
условию задачи определитель должен
равняться ![]() ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]() .
.

Линейные операции над матрицами
Тема: Линейные операции над матрицами
Дана
матрица
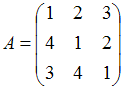 .
Если
.
Если
![]() ,
то матрица
,
то матрица
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
умножении матрицы на число каждый
элемент матрицы умножается на данное
число. При сложении или вычитании матриц
одинаковой размерности соответствующие
элементы матриц складываются или
вычитаются друг из друга. В данном
случае:
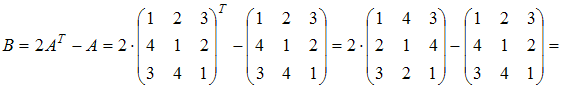
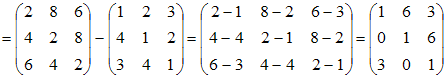
Тема: Умножение матриц
Соотношение
![]() выполняется,
только для …
выполняется,
только для …
|
|
|
перестановочных матриц |
|
|
|
единичных матриц |
|
|
|
диагональных матриц |
|
|
|
нулевых матриц |
Решение: Соотношение выполняется, то такие матрицы называются перестановочными.
Тема: Линейные операции над матрицами
Дана
матрица
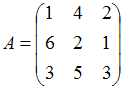 .
Если
.
Если
![]() ,
где
,
где
![]() –
единичная матрица того же размера, что
и матрица
–
единичная матрица того же размера, что
и матрица
![]() ,
то матрица
равна …
,
то матрица
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Матрица
находится
следующим образом:
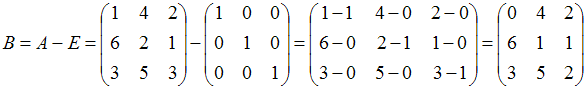 .
.
Тема: Линейные операции над матрицами
Даны
матрицы
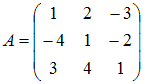 и
и
 .
Тогда решением уравнения
.
Тогда решением уравнения
![]() является
матрица
является
матрица
![]() ,
равная …
,
равная …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Линейные
операции над матрицами
Матрицы ![]() имеют
одинаковую размерность. Если
–
единичная матрица того же размера, что
и матрицы
,
и матрица
имеют
одинаковую размерность. Если
–
единичная матрица того же размера, что
и матрицы
,
и матрица ![]() ,
тогда верно равенство …
,
тогда верно равенство …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Если выразить матрицу , то получим равенство: .
Тема:
Умножение
матриц
Даны
матрицы 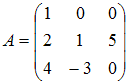 и
и 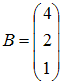 .
Тогда матрица
.
Тогда матрица ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Произведением ![]() матрицы
размера
матрицы
размера ![]() на
матрицу
на
матрицу ![]() размера
размера ![]() называется
матрица
называется
матрица ![]() размера
размера ![]() ,
элемент которой
,
элемент которой ![]() равен
сумме произведений соответственных
элементов i-й
строки матрицы
и
j-го
столбца матрицы
.
То
есть
равен
сумме произведений соответственных
элементов i-й
строки матрицы
и
j-го
столбца матрицы
.
То
есть 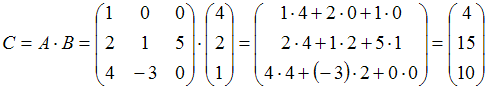 .
.
Тема: Обратная матрица
Для
матрицы
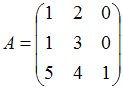 обратная
матрица равна …
обратная
матрица равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Обратная
матрица имеет вид
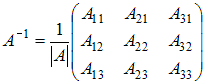 ,
вычислим
,
вычислим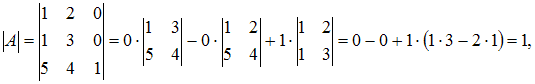
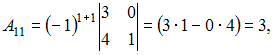
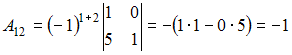
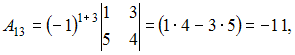


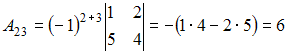
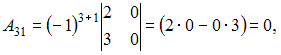
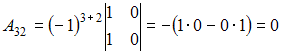
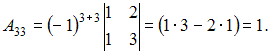 Получается,
что
Получается,
что
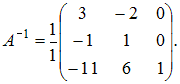
Тема: Обратная матрица
Для
матрицы
![]() существует
обратная, если она равна …
существует
обратная, если она равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Всякая
невырожденная квадратная матрица имеет
обратную матрицу, то есть матрица имеет
обратную, если определитель матрицы не
равен нулю, тогда
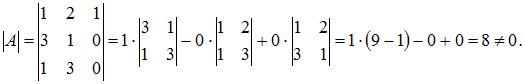
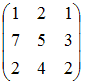
Тема: Ранг матрицы
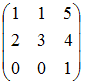
Дана
матрица
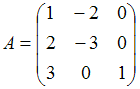 .
Тогда ранг матрицы
.
Тогда ранг матрицы
![]()
|
|
|
равен 3 |
|
|
|
равен 1 |
|
|
|
равен 0 |
|
|
|
не определен |
Решение:
Рангом
матрицы называется наибольший из
порядков ее миноров, не равных нулю.
1)
Проверим существование обратной
матрицы
![]() ,
для чего вычислим определитель матрицы
(разложением
по третьему столбцу)
,
для чего вычислим определитель матрицы
(разложением
по третьему столбцу)
 ,
следовательно обратная матрица
существует.
2) Тогда матрица
,
следовательно обратная матрица
существует.
2) Тогда матрица
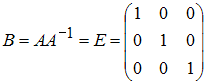 ,
то есть единичной матрице размерности
3×3. Следовательно, существует ненулевой
минор третьего порядка:
,
то есть единичной матрице размерности
3×3. Следовательно, существует ненулевой
минор третьего порядка:
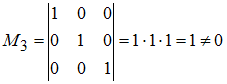 ,
то
есть ранг матрицы равен трем.
,
то
есть ранг матрицы равен трем.
Тема: Обратная матрица
Если
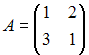 ,
,
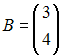 ,
то решение матричного уравнения
,
то решение матричного уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Обратная матрица Если , , то решение матричного уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решение
матричного уравнения имеет вид:![]() ,
где
,
где
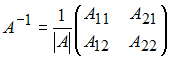 –
обратная матрица.
Вычислим
последовательно
–
обратная матрица.
Вычислим
последовательно 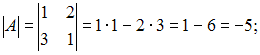
![]()
![]()
![]()
![]() Тогда
Тогда 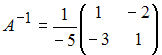 .
Следовательно,
.
Следовательно, 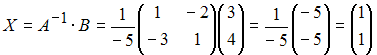 .
.