Решение.

В примере 3 нашли, что оценки для математического ожидания (среднего) и дисперсии результатов измерений равны ; , следовательно, , тогда Ф^-1 Ф^-1(0,93) = 1,3468.

Доверительные границы ,

.

Доверительный интервал 221,49).

Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону

В данном пункте были рассмотрены грубо приближенные методы построения доверительных интервалов для математического ожидания и дисперсии. Для точного нахождения интервалов совершенно необходимо знать заранее вид закона распределения величины Х, тогда как для применения приближенных методов это не обязательно. Идея точных методов построения доверительных интервалов сводится к следующему. Любой доверительный интервал находится из условия, выражающего вероятность выполнения некоторых неравенств, в которые входит оценка . Закон распределения оценки в общем случае зависит от самих неизвестных параметров величины Х. Однако иногда удается перейти в неравенствах от случайной величины к какой-либо другой функции наблюдаемых значений Х₁, Х₂,…, Х_n, закон распределения которой не зависит от неизвестных параметров, а зависит только от числа опытов n и от вида закона распределения величины Х. Наиболее подробно такие случайные величины изучены для случая нормального распределения величины Х.

Доказано, что при нормальном распределении величины Х случайная величина , где 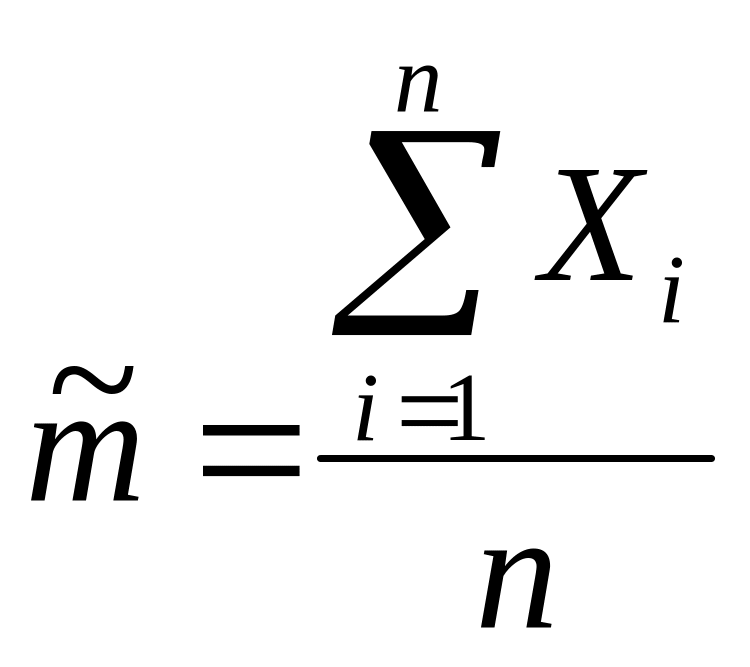, , 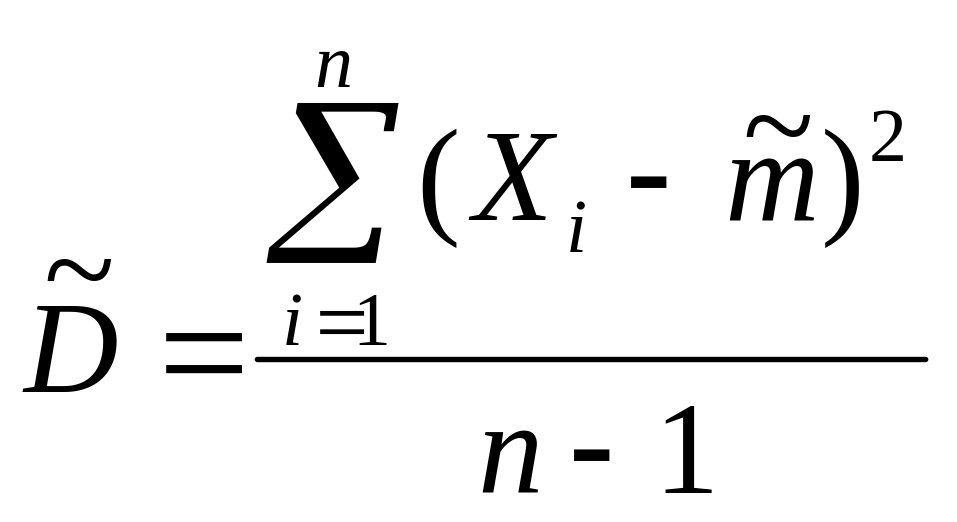подчиняется закону распределения Стьюдента с n–1 степенями свободы; плотность этого закона имеет вид 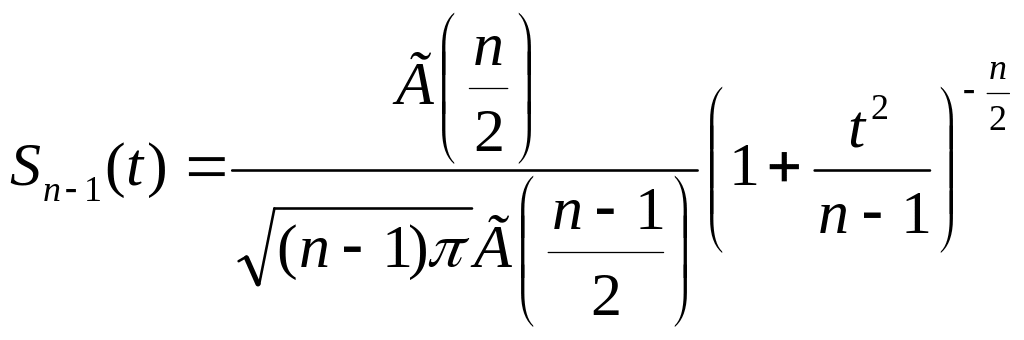, где Г(х) – известная гамма-функция .

Доказано также, что случайная величина имеет распределение «хи-квадрат» (Пирсона) с n–1 степенями свободы; плотность которого выражается формулой .

Для построения доверительного интервала для мат.ожидания в равенстве (*) от случайной величины необходимо перейти к случайной величине Т, распределенной по закону Стьюдента. Доверительный интервал в этом случае выражается формулой ; величина находится из условия 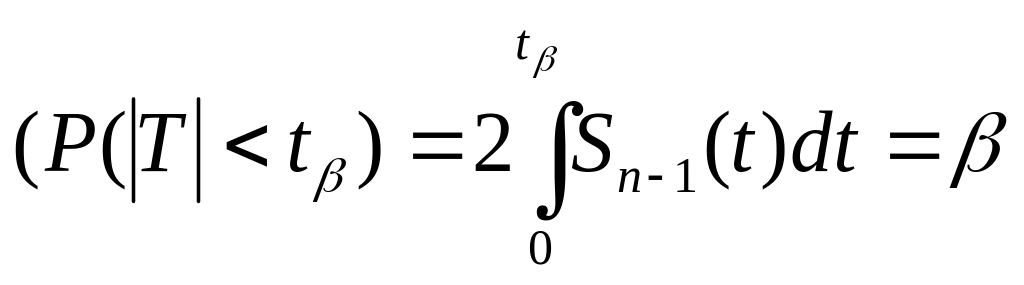. Существуют таблицы значений в зависимости от доверительной вероятности и числа степеней свободы n–1.

Выразим случайную величину через величину V, имеющей распределение , тогда доверительный интервал для дисперсии выражается формулой 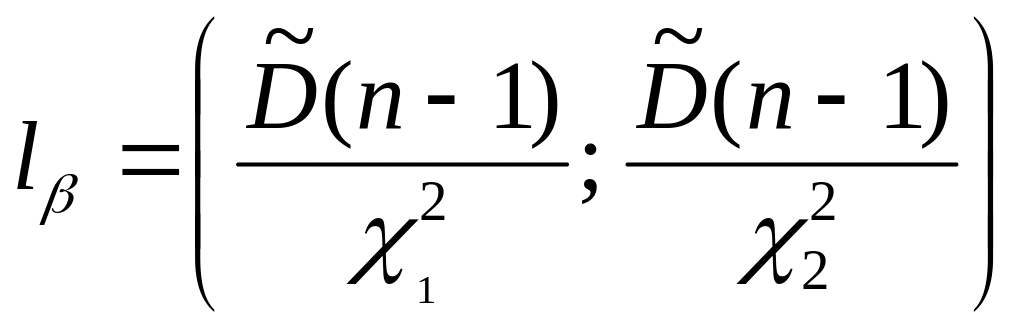, где и соответственно левый и правый концы интервала , в который величина V попадает с заданной вероятностью .

П. 8. Корреляция

Теория корреляции применяется, как нам уже известно, для установления связи между двумя случайными величинами Х и У и для установление тесноты этой связи. Х и У могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Определение 29. Статистической называют зависимость, при которой изменение одной из величин влечет за собой изменение закона распределения другой.

Определение 30. Статистическая зависимость называется корреляционной, если при изменении одной из величин изменяется среднее значение другой.

Определение 31. Условным средним называется среднее арифметическое наблюдавшихся значений случайной величины У, соответствующих Х = х.

Определение 32. Уравнение называется выборочным уравнением регрессии У по х.

Аналогично даются определения условного среднего и выборочного уравнения Х по у .

Условные средние и , которые находятся по выборке, принимают в качестве оценок условных математических ожиданий и .

Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной. Для нормально распределенного вектора (Х, У) теоретические уравнения регрессии – линейные:

, ,

где и – выборочные средние случайных величин У и Х, и – выборочные средние квадратические отклонения, выборочный коэффициент корреляции.

. Величина характеризует, насколько близка связь между Х и У к линейной зависимости : 1) если , то считают, что линейной зависимости нет. 2) Чем ближе к 0, тем связь слабее; чем ближе к 1, тем связь сильнее: если, , то линии регрессии сливаются в одну линию, а случайные величины X и Y связаны между собой линейной функциональной зависимостью.

Определение 32. Уравнение называется выборочным уравнением парной регрессии.

Рассмотрим уравнение и найдем связь между коэффициентами уравнения и выборочными средними квадратическими отклонениями и выборочным коэффициентом корреляции. Для этого преобразуем уравнение:

и сравним с уравнением , отсюда

, , следовательно, выборочный коэффициент корреляции равен

. (14)

Замечание. Аналогично рассматривается выборочное уравнение парной регрессии .

Пример. Дано выборочное уравнение парной регрессии и выборочные средние квадратические отклонения и . Найти выборочный коэффициент корреляции.