Вторая задача: Задача о содержании.

Рассмотрим эту задачу в постановке задачи о питании студента.

Для того, чтобы студент мог нормально учиться и не попал в больницу, для этого необходимо, чтобы он получал 100 грамм жиров, 30 грамм углеводов и 5 грамм белков (цифры условные). Для этого студент закупил большое количество продуктов, которые он может брать в любых количествах, а именно суп, колбасу, шоколад, пиво.

Кг	Жиры	Углеводы	белки
Суп (150 р)	150	20	2
Колбаса (350 р)	50	30	4
Шоколад (500 р)	300	100	1
Пиво (100 р)	-	60	1

При этом за кг супа студент платит 150 рублей. Вопрос: составить такой рацион питания студента, чтобы он не умер с голоду (получал вещества в не меньших количествах), но чтобы затраты были минимальные.

Математическая модель задачи

Обозначим в кг рацион питания Х1, Х2, Х3 и Х4. Тогда функция цели

Z=150*X1+350*X2+500*X3+100*X4. Тогда очевидно, что если Х≥0, то ответ равен нулю. Нужны ограничения.

Ограничения по жирам ~ 150*Х1+50*Х2+300*Х3 ≥ 100

Ограничения по углеродам ~ 20*X1+30*X2+100*X3+60*X4 ≥30

Ограничения по белкам ~ 2*X1+4*X2+1*X3+1*X4 ≥5

Замечание: в такой постановке (берем любое количество продуктов) задача линейная, однако если студент питается в столовой, продукты покупает, то суп он может брать кратно пол порции X1={0,2; 0,4; 0,6; 0,8, 1}. Суп X3 ={0,1; 0,2; 0,3; 0,4}. Колбаса Х3={любое}. Пиво X4={0,25; 0,5…}В этом случае задача становится существенно не линейная.

Задача о смеси

Возьмем нефтяную постановку.

Нефтеперерабатывающий завод выпускает 3 сорта бензина: А-80, А-92, А-95. И продает по следующим ценам за тонну: 25, 28, 30. Бензины производятся путем смешивания (примем, что без потерь массы) следующих 4-ех продуктов: алкилат 300 тонн, бензин прямой перегонки 200 тонн, крекинг бензин 150 тонн, изопентан 50 тонн.

Если смешать наши вещества в пропорциях 5:3:2:1, то получим А-80, если 3:2:2:1, то получим А-92, если 2:1:3:2, то получим А-95.

Вопрос: каких сортов, и какие бензины изготавливать, и сколько, чтобы получить максимум суммарного дохода?

Возможный вариант модели.

Обозначим Х1,Х2,Х3 в тоннах выпуск соответствующего бензина, тогда доход будет иметь следующий вид max d = 25*X1+28*X2+30*X3.

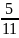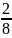Ограничение по алкитату X1+ X2+ X3 ≤ 300

П X1+ X2+ X3 ≤200

К X1+ X2+ X3 ≤150

И X1+ X2+ X3 50

Задача о смеси линейная

Транспортная задача.

Пусть имеется 3 склада, на которых соответственно имеется 100, 80 и 120 единиц продукции. Пусть имеется 4 потребителя этой продукции, которые требуют не меньше чем 40, 160, 20, 80 ед продукции. !Заданно затраты на перевозку единицы продукции от каждого поставщика к каждому потребителю.

Сколько стоит переслать единицу продукции:

Поставщик 1	2	3	1	4
Поставщик 2	12	10	14	9
Поставщик 3	25	23	24	22

Вопрос: Определить такой план перевозки, чтобы затраты были минимальные (сколько кому вести)?

Модель задачи

X_ij от поставщика i к потребителю j

X₁₁ X₁₂ X₁₃ X₁₄

X₂₁ X₂₂ X₂₃ X₂₄

X₃₁ X₃₂ X₃₃ X₃₄

Минимум затрат minz= 2X₁₁ + 3X₁₂ + 1X₁₃ + 4Х₁₄+ X₂₁ X₂₂ X₂₃ X₂₄+ X₃₁ X₃₂ X₃₃ X₃₄

Условия по потребителям X₁₁+ X₂₁+ X₃₁ ≥40

Ограничения по запасам поставщиков

X₁₁ X₁₂ X₁₃ X₁₄ ≤100

X₂₁ X₂₂ X₂₃ X₂₄ ≤80

X₃₁ X₃₂ X₃₃ X₃₄ ≤120

Потребители просят не меньше, но в результате решения задачи получат ровно нижнюю границу (40, 160, 20 и 80), так как больше этих величин давать нет смысла ибо затраты возрастут, отсюда ограничения по поставщикам превратятся в равенства. В нашем случае, суммарное потребление, 300, но и у поставщиков 300. Следовательно, у поставщиков после транспортировки ничего не останется. И ограничения можно тоже напить равенства. Такая задача называется сбалансированной (замкнутой транспортной задачей). Существует 3 вида задач транспортных:

1. Когда суммарный запас равен суммарному спросу, задача на минимум, ограничение только равенство.

2. Суммарный запас больше суммарного спроса. Задачи этого типа легко сводятся к сбалансированной задаче путем введения фиктивного потребителя с потребностью (сумма запасов минус сумма спроса). Затраты к нему нулевые и все, что он получит, останется у поставщика.

3. Социалистическая – запасы меньше спроса. Такая задача не имеет никакого решения. Можно решить совершенно другую задачу: как развести то, что есть с недопоставками, так называемым буферным потребителям, для которых вводится коэффициент важности, умножаемый на затраты.

Транспортная задача – ЗЛП. Она обладает такими свойствами, что с её помощью можно решать:

1. Не классические транспортные задачи, т.е. задачи с промежуточным хранением, с перевозками между поставщиками и возвратом от потребителей.

2. Поиск кратчайшего пути в сети для задач календарного планирования и управления.

3. Задача о назначении. Имеются работы и исполнители работ, заданы затраты на выполнение каждым исполнителем каждой работы, так чтобы затраты были минимальные.

Задача математического программирования.

max

05.03.12

Геометрическая интерпретация поиска оптимальной точки.

Пример:

Max L=X1+3X2

6X1+5X2<=30

X1+2X2<=6

X1+X2=>1

X1=>0

X2=>0

AX1+bX2<=C

aX1+bX2=C – прямая, на этой прямой имеем строгие равенства, вопрос: какие точки удовлетворяют этому неравенству

6X1+5X2<=30

6X1+5X2=30

X1=0, X2=6

X2=0, X1=5

\

Область ограничения данной задачи – это все точки внутри и на границе многоугольника ABKDE.

Значит любая точка (а их бесконечное множество) является допустимой точкой задач, из которых будем искать оптимальную.

Экономический смысл допустимой точки (все возможные допустимые варианты параметров экономической задачи), а оптимальная точка только один наилучший по функции цели или по критерию принятия решения.

Поиск оптимальной точки из допустимых

L=X1+3X2

Пусть L=4

X1+3X2=4

X2=0, X1=4

X1=0, X2=1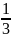

Если нарисовать семейство прямых L=Const, то они образуют так называемые линии равного уровня. Эти линии параллельны между собой и их легко построить, если взять вектор C= (вектор коэффициентов функции цели) этот вектор называется вектором Градиента, он перпендикулярен линиям равного уровняю.

Вектор С своим направлением показывает возрастание функции цели, поэтому если двигать перпендикуляры по стрелке вектора С, то крайняя (последняя) точка области допустимых значений – это максимум (в нашем случае точка К), если двигать против стрелки градиента, то это точка минимум (точка А).

Если первое ограничение равенства, то область допустимых значений отрезов DE.

Геометрическая интерпретация показывает, что возможно, что оптимальное решение задачи линейного программирования – это угловая точка области допустимых значений.

Виды областей допустимых значений в линейном программировании (ЗЛП):

1. Ограниченная выпуклая область

(1)

(2)

(3)

33(

ЗЛП дает только выпуклую область. Область называется выпуклой, если отрезок, соединяющий её точки принадлежит ей. Круг является выпуклой, но не окружность!!!

2. Неограниченный выпуклый многогранник

(4)

(5)

3. Отсутствие допустимых точек (нету точек, которые удовлетворяют решению).

В задачах экономики и управления могут встречаться только ситуации 1, 2 и тривиальная ситуация 3.

Ситуация 4 и 5 в экономике не встречается из-за ограниченности ресурсов (материалы, время, деньги).

Ситуация 6 для функционирующего объекта не встречается, она может встретиться только при планировании. Когда неизвестно хватит ли ресурсов для функционирования объекта.

Ситуации с поиском оптимального решения ЗЛП.

1. Е динственное оптимальное решение – угловая точка вершины многогранника.

max

min

2. Б есконечное множество оптимальных точек (грань многогранника) альтернативный оптимум.

A

В

min А B

А и В max все допустимые точки оптимальны

Для принятия решения в альтернативном случае берется любая точка из оптимальных (наилучших данной задачи). Её выбирают из вне модельных соображений.

3. О тсутствие оптимального решения на множестве допустимых в экономике и управлении не встречается.

Мин и макс нет

4. Нет допустимых точек.

Теорема об оптимальном решении ЗЛП.

Если задача линейного программирования имеет оптимальное решение (для ограниченного многогранника всегда), то это решение, либо единственное – угловая точка, либо этих решений бесконечное множество на грани многогранника, среди, которых есть угловые точки. Т.о. всегда среди оптимальных точек, есть угловая.

Экономический смысл угловой точки.

А I-ресурс

В

О

Е

II-ресурс

В точке А оба ресурса расходуются полностью.

В угловых точках полностью расходуется некое количество ресурса (на плоскости 2), либо расходуется ресурс полностью и не выпускается продукт (точка В – полностью 1 ресурс, не выпускается 2-ой продукт).

Для поиска оптимального решения необходимо проверить угловые точки, они подозрительны на оптимальность.

Легко доказать, что угловых точек – конечное число.

Поиск оптимальной точки из перебора бесконечного множества допустимых точек сводится к перебору конечного числа угловых точек.

Для построения угловых точек задач с двумя переменными – нет никаких проблем, это легко делается на плоскости. Если же задача имеет больше, чем 2 переменные, возникает проблема поиска угловой точки.

Определение: точка в любом пространстве для выпуклового множества линейного многогранника называется угловой, если она не может быть внутренней точкой любого отрезка этого множества.