6. Оценка согласованности мнений экспертов

При ранжировании объектов эксперты обычно в большей или меньшей степени расходятся во мнениях по решаемой проблеме. В связи с этим возникает необходимость количественной оценки степени согласия экспертов. Получение количественной меры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины в расхождении мнений.

Известны две меры согласованности мнений группы экспертов: дисперсионный и энтропийный коэффициенты конкордации [12, 43].

Сравнительная оценка дисперсионного и энтропийного коэффициентов показывает, что эти коэффициенты дают примерно одинаковую оценку согласованности экспертов при близких ранжировках. Однако если, например, вся группа экспертов разделилась во мнениях на две подгруппы, причем ранжировки в этих подгруппах противоположные (прямая и обратная), то дисперсионный коэффициент конкордации будет равен 0, а энтропийный коэффициент конкордации будет равен 0,7. Таким образом, энтропийный коэффициент конкордации в отличие от дисперсионного позволяет зафиксировать факт разделения мнений на две противоположные группы.

В данной работе принято решение использовать энтропийный коэффициент конкордации (коэффициент согласия).

6.1. Энтропийный коэффициент конкордации (коэффициент согласия)

Коэффициент согласия определяется формулой:

(6.1)

где H – энтропия, вычисляемая по формуле [42]:

(6.2)

а H_max – максимальное значение энтропии.

Здесь N число объектов ¹¹,

L число экспертов,

F_n(L) число групп экспертов, присвоивших объекту O_n один и тот же ранг r_nl.

В формуле (6.2) p_nl – оценка вероятности того, что l‑ая группа экспертов присвоит n‑му объекту один и тот же ранг r_nl. Эта оценка вычисляется в виде отношения количества экспертов L_nl, приписавших объекту O_n один и тот же ранг r_nl, к общему числу экспертов L:

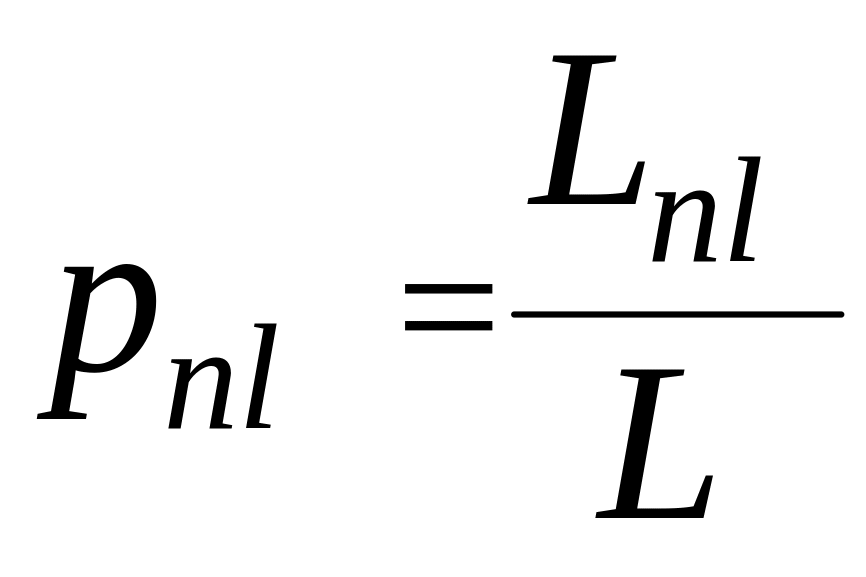(6.3)

6.2. Матрица, определяющая наибольшие расхождения экспертов

Определяется матрица L_nl размером N*N, позволяющая зафиксировать группы L_nl, например:

Матрица 1 (Lnl)

	O1	O2	O3	O4
r=1	0	0	1	3
r=2	1	2	2	0
r=3	1	1	0	0
r=4	1	0	0	0
∑	3	3	3	3

Матрица L_nl обладает следующим свойством:

(6.4)

В приведенном выше примере число объектов равно 4, число экспертов равно 3. Максимальное значение ранга равно числу объектов. Элемент матрицы L_nl определяет число экспертов, присвоивших объекту O_n один и тот же ранг r_nl.

В данном примере наибольшее согласие экспертов наблюдается по объекту O₄ (все эксперты присвоили ему один и тот же ранг); наименьшее – по объекту O₁ (мнения всех экспертов различны).

6.3. Максимальное значение энтропии

Для определения максимального значения энтропии определим:

Q = Round (L/N), т. е. целое частное от деления числа экспертов на число объектов,

R = L Mod N, т. е. остаток от деления числа экспертов на число объектов. Таким образом, L = N × Q + R.

Тогда число объектов, получивших по Q единиц:

А число объектов, получивших по Q + 1 единиц:

Тогда

(6.5)

Если Q = 0, то L = R и H_max^Q = 0.

Тогда

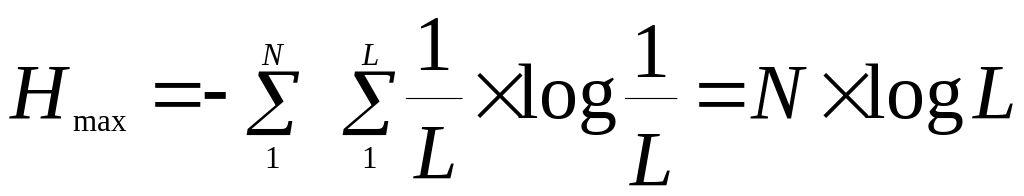(6.6)

Если Q ≥ 1, то:

(6.7)

В качестве иллюстрации рассмотрим случай, когда число экспертов равно 6, а число объектов равно 4, т.е., L = 6, N = 4. Тогда частное Q = 1, остаток R = 2. Матрица L_nl для вычисления H_max примет вид:

Матрица 2 (Lnl)

	O1	O2	O3	O4
r=1	2	2	2	2
r=2	2	2	2	2
r=3	1	1	1	1
r=4	1	1	1	1
∑	6	6	6	6

Коэффициент согласия изменяется от 0 до 1. При W_э = 0 расположение объектов по рангам равновероятно, поскольку в этом случае H = H_max. Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупности показателей, либо полной несогласованностью мнений экспертов. При W_э = 1, что достигается при нулевой энтропии (H = 0), все эксперты дают одинаковую ранжировку. Действительно, в этом случае для каждого фиксированного объекта O_n все эксперты присваивают ему один и тот же ранг. Следовательно, p_nl = 1, а p_kl = 0, (k ≠ l, k = 1,2, …, N). Поэтому и H = 0.

В качестве примера рассмотрим экспертные оценки (предпочтительности) целей для задачи «Оптимизация организационной структуры второго уровня управления городом». Для решения задачи привлечены три эксперта (таблица 6.1):

Таблица 6.1. Список экспертов

Номер	Имя эксперта	Вес эксперта
1	Миронов	7
2	Блинов	5
3	Кириллов	4

Рассматриваемая проблемная ситуация может развиваться по двум сценариям (таблица 6.2):

Таблица 7.2. Перечень возможных ситуаций и их весов

Номер ситуации	Название ситуации	Вероятность
1	Изменения структуры управления могут затронуть распределение функций между комплексами	10
2	Изменения допустимы только внутри комплексов	2

Ниже приводится перечень целей (таблица 6.3).

Таблица 6.3. Перечень целей

Номер цели	Название цели
1	Повышение эффективности принимаемых решений
2	Повышение оперативности принимаемых решений
3	Повышение ответственности исполнителей за подготовку решений
4	Сокращение численности органов исполнительной власти второго уровня управления
5	Минимизация материальных, моральных и финансовых издержек в переходном периоде проводимых преобразований

Предпочтительности целей определяются каждым экспертом для каждой ситуации в ранговой шкале (таблица 6.4):

Таблица 6.4. Ранжировка целей экспертами

Эксперт 1	Миронов
	Предпочтительности целей↓
№№ целей→	1	2	3	4	5
№№ ситуаций↓
1	1	2	3	5	5
2	1	2	2	3	5
Эксперт 2	Блинов
	Предпочтительности целей↓
№№ целей→	1	2	3	4	5
№№ ситуаций↓
1	2	3	3	4	5
2	2	3	3	5	5
Эксперт 3	Кириллов
	Предпочтительности целей↓
№№ целей→	1	2	3	4	5
№№ ситуаций↓
1	2	2	1	4	5
2	2	2	1	3	5

Для каждой ситуации вычисляется коэффициент согласия экспертов (согласованность значимостей целей), а также строится матрица 1, позволяющая определить расхождения в мнениях экспертов (таблица 6.5).

Таблица 6.5. Согласованность значимости целей

	Ситуация 1: Изменения структуры управления могут затронуть респределение функций между комплексами
	Согласованность значимостей целей: 0,67
	Число экспертов, присвоивших цели один и тот же ранг ↓. Максимальное расхождение мнений экспертов - для цели 1, цели 2, цели 3, цели 4
	№№ целей→	1	2	3	4	5
	Ранги↓
	1	1	0	1	0	0
	2	2	2	0	0	0
	3	0	1	2	0	0
	4	0	0	0	2	0
	5	0	0	0	1	3
Ситуация 2: Изменения допустимы только внутри комплексов
Согласованность значимостей целей: 0,61
Число экспертов, присвоивших цели один и тот же ранг ↓. Максимальное расхождение мнений экспертов - для цели 3
№№ целей→		1	2	3	4	5
Ранги↓
1		1	0	1	0	0
2		2	2	1	0	0
3		0	1	1	2	0
4		0	0	0	0	0
5		0	0	0	1	3