0 В противном случае
Далее в соответствии с количеством единиц в каждой строке матрицы С строится окончательная ранжировка вариантов решений. Важным свойством принципа медианы является то, что объект, являющийся наилучшим по принципу медианы, является своеобразным центром среди всех сравниваемых объектов. Матрица парных сравнений (медиана) имеет минимальное расстояние Хемминга [11] от всех сравниваемых объектов. Смысл индексов в приведенных формулах тот же, что и в описании принципа Парето. Приведем пример применения метода медианы.
5.3.4. Пример применения метода медианы
Коррупция в нашей стране не просто приобрела масштабный характер. Она стала привычным, обыденным явлением, которое характеризует саму жизнь нашего общества. Речь идет не просто о банальных взятках. Речь о тяжелой болезни, которая съедает экономику и разлагает все общество. Этот вид преступлений действительно латентен и практически не поддается статистическому учету.
В материалах общественной палаты определены зоны поражения коррупцией [67]. Это бытовая коррупция, коррупция в органах власти, коррупция в судебных, правоохранительных и контролирующих органах, политическая коррупция. Однако действия власти и общества по преодолению коррупции не приводятся. Вместе с тем, необходимо не только четко сформулировать эти меры, но и определить их приоритетность с точки зрения достижения глобальной цели - улучшение качества жизни населения. Качество жизни населения - сложная синтетическая категория, зависящая от множества факторов. В настоящее время наиболее распространенным и обоснованным является определение качества жизни населения с помощью 5 категорий второго уровня [2, 15]: качество населения, благосостояние населения, качество социальной сферы, качество экологической ниши и природно-климатические условия (рис. 5.2).
С нашей точки зрения генеральной целью борьбы с коррупцией является повышение качества жизни населения с точки зрения упомянутых выше категорий. Природно-климатические условия здесь обсуждаться не будут.
В соответствии с разделом 1, определим основные объекты процесса выбора решения.
Рассматриваются меры по преодолению четырех зон поражения коррупцией:
Меры по преодолению бытовой коррупции (Y1).
Меры против коррупции в органах власти (Y2).
Меры против коррупции в судебных и правоохранительных органах (Y3).
Меры против политической коррупции (Y4).
Следует выполнить ранжирование этих мер по совокупности перечисленных выше четырех категорий повышения качества жизни населения второго уровня (G1, …, G4), перечисленных в таблице 5.1. Ранги категорий присвоены экспертами.
Таблица 5.1. Ранжировка мер по преодолению коррупции
|
Ранг |
Вес |
Категория |
Y1 |
Y2 |
Y3 |
Y4 |
G1 |
1 |
4 |
Повышение качества населения |
2 |
4 |
1 |
3 |
G2 |
3 |
2 |
Повышение благосостояния населения |
1 |
3 |
2 |
4 |
G3 |
2 |
3 |
Повышение качества социальной сферы |
1 |
2 |
3 |
4 |
G4 |
4 |
1 |
Улучшение качества экологической ниши |
2 |
1 |
4 |
3 |
В таблице 5.2 приведены те же категории. Они теперь для удобства вычислений расположены в столбцах. Ранги категорий преобразованы в коэффициенты относительной важности (веса). Нормализованные значения весов представлены в последней строке таблицы. Нормализация производится по формуле (5.14), где w[j] – нормализованное значение веса, b[j] – ненормализованные значения весов.
w[j] = b[j] / (b[1]+b[2]+...+b[M]) (5.14)
Легко убедиться, что w[1]+w[2]+...+w[M]= 1
Например, нормализованный вес первой категории (G1) вычисляется следующим образом (таблица 5.2):
Вес = 4 / (4 + 2 + 3 + 1) = 0,4
Для каждой строки каждой из четырех матриц парных сравнений выполним преобразование векторов рангов, используя правило
Fij = 1, если Yij ≥ Yik
Fij = 0 в противном случае (5.15)
Таблица 5.2. Подготовка данных для вычисления медианы
|
G1 |
G2 |
G3 |
G4 |
Y1 |
2 |
1 |
1 |
2 |
Y2 |
4 |
3 |
2 |
1 |
Y3 |
1 |
2 |
3 |
4 |
Y4 |
3 |
4 |
4 |
3 |
Вес |
0,4 |
0,2 |
0,3 |
0,1 |
В результате получим матрицы парных сравнений, приведенные на рис. 5.3, по каждой из рассматриваемых категорий (целей).
Далее выполним поэлементное умножение каждой матрицы на нормализованный вес каждой из категорий и произведем поэлементное суммирование всех матриц. Получим матрицу, обозначенную как «Сумма».
Преобразуя эту матрицу по правилу (5.15), получим матрицу M, которая и является матрицей–медианой. Суммируя элементы матрицы M по столбцам, получим результат, приведенный справа от матрицы M.
Таким образом, первый ранг (место) получают меры по преодолению бытовой коррупции, второй ранг – меры против коррупции в судебных и правоохранительных органах, третий ранг – меры против коррупции в органах власти и, наконец, последнее, четвертое место занимают меры против политической коррупции.
Далее вычисляются поразрядные несовпадения матриц G1–G4 с медианой M и расстояние Хемминга (H) для каждой из этих матриц. Вычисления даны в правой части рисунка 5.3.
На рис. 5.4 приведены результаты эксперимента: изменен один из элементов матрицы–медианы M (определите, какой). Как изменились значения расстояний Хемминга (H)? Сравните результаты с выкладками (5.2)–(5.12).
Рис. 5.3. Вычисление медианы (M) и расстояний Хемминга (H)
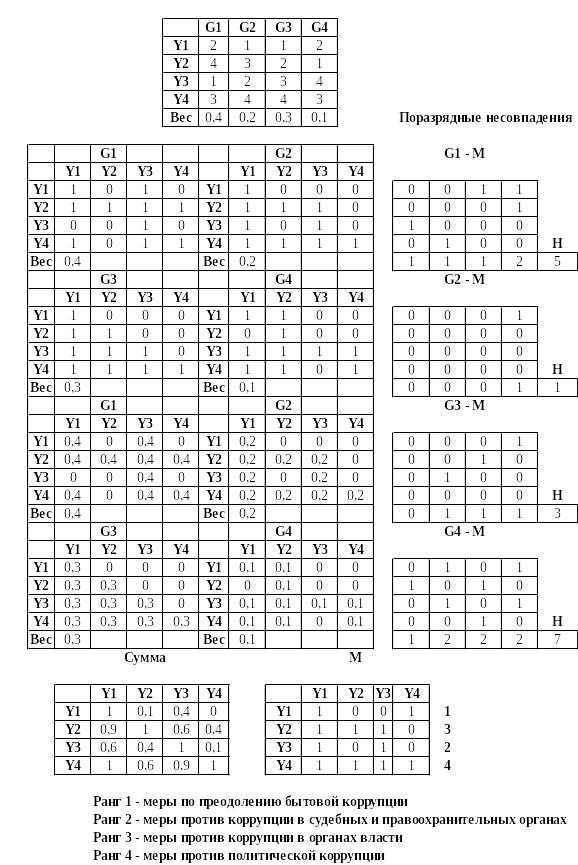
Рис. 5.4. Изменение расстояний Хемминга (H) при изменении медианы (M)