5.3.2.Описание критерия Гурвица

Критерий Гурвица называют иначе критерием «пессимизма-оптимизма». Для его применения достаточно иметь оценки (т.е., значения функции предпочтения) в виде рангов.

Критерий пессимизма (гарантированный результат) – «рассчитывай на худшее»:

Для каждого t-го из N вариантов решений по всем экспертам, всем ситуациям и всем целям выбирается наихудшее значение функции предпочтения, т.е., максимальный ранг. «Лучшим» признается то решение, у которого этот ранг наименьший (т.е., «лучший из худших»):

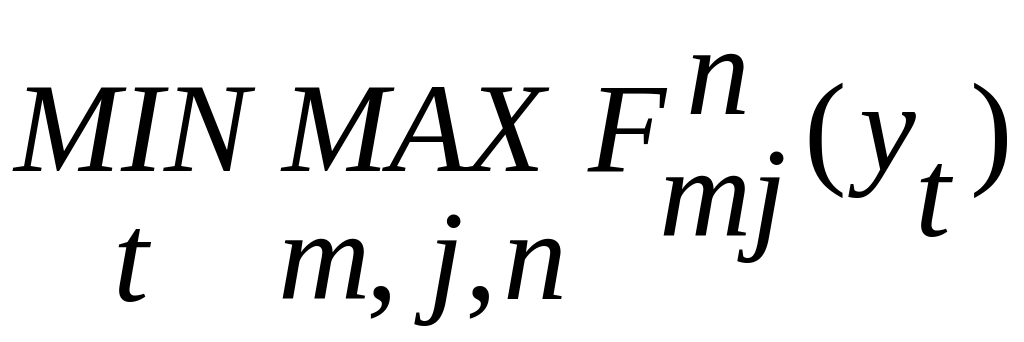
Критерий оптимизма – «рассчитывай на лучшее»:

Здесь выбирается «лучший из лучших». Решение имеет вид:

Собственно критерий Гурвица

Обобщенный критерий является взвешенной комбинацией критериев пессимизма и оптимизма с коэффициентом веса пессимизма h, определяемого экспертно, причем 0 ≤ h ≤ 1. При h = 0 обобщенный критерий превращается в критерий оптимизма, при h = 1 – в критерий пессимизма. Коэффициент пессимизма может рассматриваться как некоторая субъективная вероятность благоприятного развития событий, причем значение этой вероятности определяется на основании усреднения мнений всех членов экспертной группы.

Упорядочение решений с помощью критерия Гурвица:

По критерию пессимизма строятся упорядочение вариантов решений согласно их рангам (значениям функции предпочтения):

r₁, r₂, … ,r_N

и соответствующую этому упорядочению матрица парных сравнений:

c_ts, t,s = 1, … , L

Аналогично, по критерию оптимизма строится последовательность

R₁, R₂, … ,R_L

и матрица C_ts.

Затем формируется матрица H_ts:

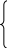1, если h* c_ts + (1-h)* C_ts ≥ 0,5

H_ts = t, s = 1, … , L

0 В противном случае

Далее определяется окончательное упорядочение решений, аналогично тому, как это было сделано для метода медианы: чем больше единиц в t-ой строке матрицы H, тем t-е решение лучше.

5.3.3. Описание метода медианы

Будем рассматривать F_mjⁿ(y_t) как ранги. Ранжировку L вариантов решений (для каждой цели j, для каждой ситуации m, для каждого эксперта n) можно представить в виде матрицы парных сравнений:

1 при F_mjⁿ(y_t) ≤ F_mjⁿ(y_s)

c_ts^jmn = t, s = 1, … , L (5.1)

0 при F_mjⁿ(y_t) > F_mjⁿ(y_s)

Матрица, которая наилучшим образом согласуется с построенными выше J*M*N матрицами парных сравнений, называется медианой. Наилучшее согласование понимается как минимальность сумм расстояний от медианы до всех матриц парных сравнений в пространстве Хемминга. В математической литературе [11] показано, что медиану можно построить с помощью расстояния Хемминга следующим способом. Пусть имеются N экспертов, соответственно N матриц парных сравнений порядка m, выражающих либо отношение, соответствующее вершинам графа, либо отношение предпочтения между целями или решениями. Эти матрицы состоят из нулей и единиц.

(s, l = 1, 2, …N), (i, k = 1, 2, m)

Тогда между матрицами R_s и R_l можно ввести метрику – расстояние Хэмминга d_sl, где

(5.2)

Смысл этого выражения состоит в том, что расстояние между матрицами парных сравнений определяется числом поразрядных несовпадений всех значений элементов матриц (метрика Хэмминга). Используя эту метрику, определим обобщенную матрицу парных сравнений как такую матрицу, которая наилучшим образом согласуется c матрицами парных сравнений, получаемыми другими экспертами. Понятие наилучшего согласования на практике чаще всего определяют как медиану.

М едиана есть такая матрица парных сравнений, сумма расстояний от которой до всех матриц парных сравнений, получаемых экспертами, является минимальной:

(5.3)

Покажем, что построение матрицы парных сравнений, соответствующей медиане, осуществляется по принципу простого большинства голосов экспертов для каждого элемента матрицы. Модуль разности переменных в формуле (5.2) равен либо единице, либо нулю, поэтому модуль разности равен квадрату этой разности. Следовательно, вместо (5.3) можно записать:

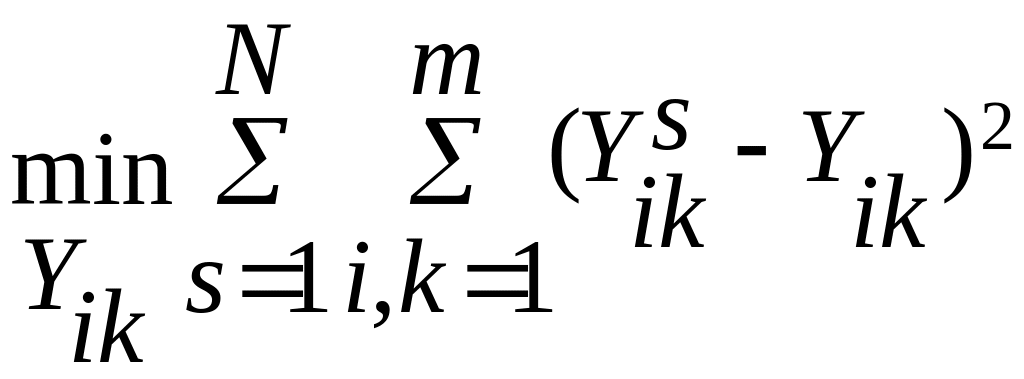
(5.4)

Возводя разность, заключенную в круглые скобки, в квадрат и учитывая, что квадрат переменной равен самой переменной, получаем из (5.4):

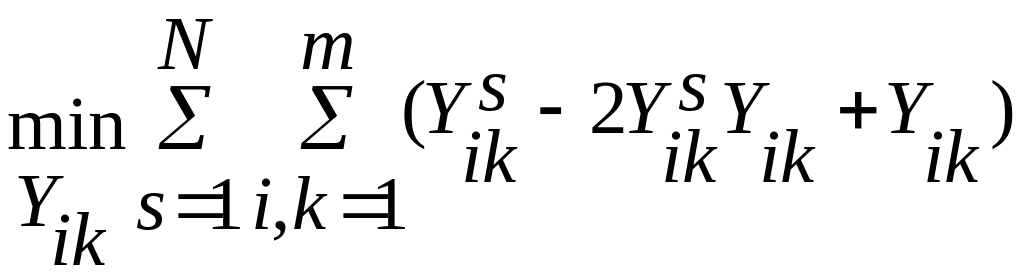
(5.5)

С уммируя по индексу s и вводя обозначение

(5.6)

получаем из (5.5)

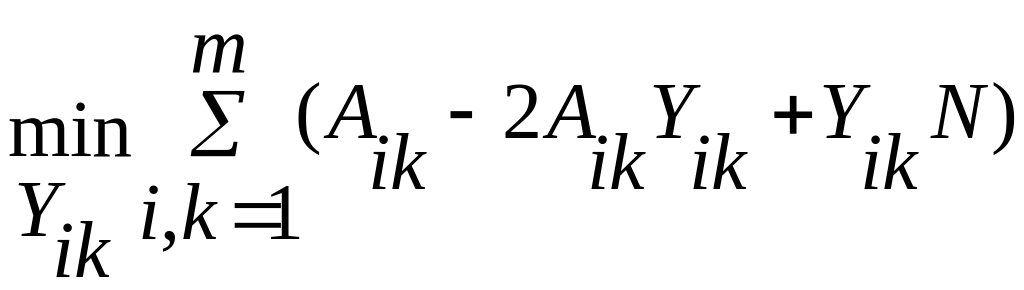
и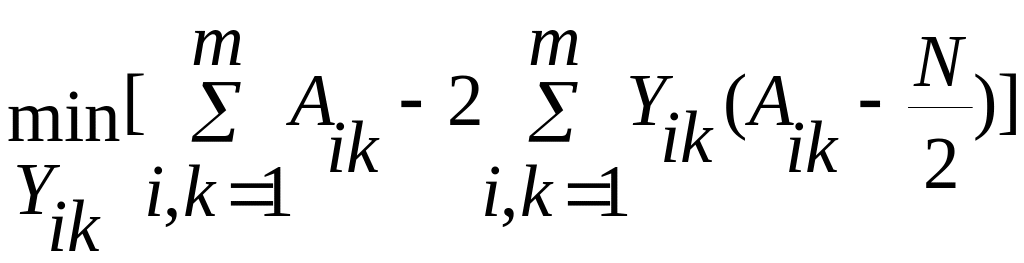 далее

(5.7)

Первая сумма в квадратной скобке постоянна и не зависит от переменной Y_ik. Поэтому минимум квадратной скобки соответствует максимуму второй суммы. Следовательно,

(5.8)

Максимум по переменным Y_ik, принимающим значения 0 или 1, достигается при следующем решающем правиле:

1, если A_ik >= N/2

Y_ik* = (5.9)

0 в противном случае

где N – количество экспертов.

Величины A_ik в соответствии с (5.6) представляют собой количество голосов, поданных экспертами за наличие бинарного отношения между i-м и k-м объектами (O). Поэтому в обобщенной матрице парных сравнений в соответствии с оптимальными правилами решения (5.8) в ik-м элементе ставится единица, т.е. принимается, что O_i R O_k, если больше половины экспертов высказались за это предпочтение. Таким образом, все элементы обобщенной матрицы парных сравнений определяются по правилу большинства голосов.

В рассмотренном алгоритме построения обобщенной матрицы парных сравнений можно учесть компетентность экспертов путем введения коэффициентов компетенции K_s в отношение (5.3):

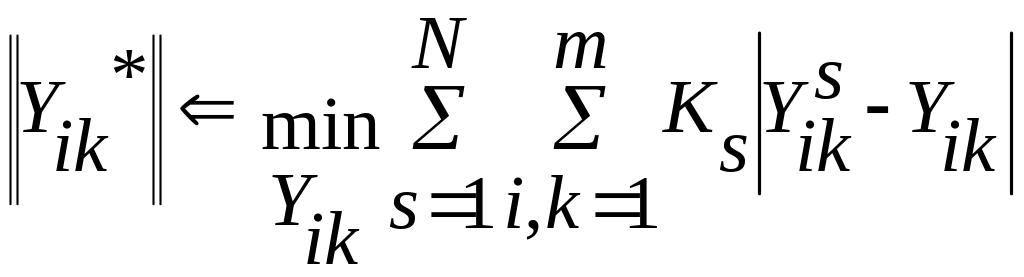
(5.10)

Выполняя преобразования, аналогичные соотношениям (5.4) – (5.9), получаем для случая учета коэффициентов компетентности экспертов следующее правило построения обобщенной матрицы парных сравнений:

1, если B_ik >= 1/2

Y_ik* = (5.11)

0 в противном случае

где величины B_ik равны

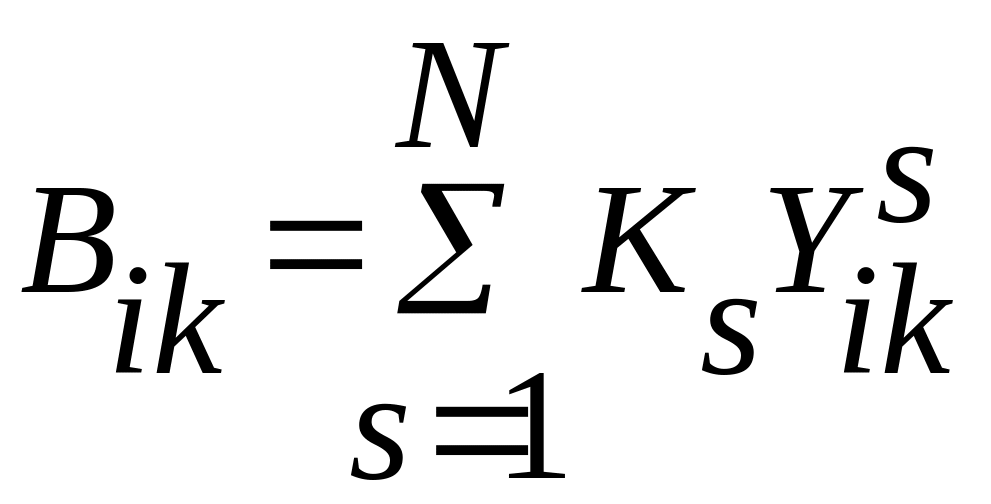(I, k = 1, 2, …, m) (5.12)

Таким образом, если эксперты обладают различной компетентностью, выраженной нормированной совокупностью «весов», можно добавить условие нормировки весов

При этом процедура определения матрицы–медианы изменяется незначительно.

Опираясь на приведенные выше рассуждения, производим следующие выкладки. Сначала строится промежуточная матрица по правилу:

Ĉ_ts = ∑_j ∑_m ∑_n kkⁿ * p_m * w_mjⁿ * c_ts^jmn

Где kkⁿ – коэффициент компетентности n-ого эксперта

p_m - вероятность m-ой ситуации

w_mjⁿ - вес j-ой цели, назначенный этим экспертом в данной ситуации

Затем строится матрица-медиана C по правилу:

1 если Ĉ_ts ≥ 0,5

C_ts = t, s = 1, … , L (5.13)