5. Выбор решений
Третий этап схемы процесса принятия решений состоит из трех процедур:
Определение допустимых решений.
Формирование принципов выбора.
Определение эффективных решений.
5.1. Определение допустимых решений
При выполнении этой процедуры возможен возврат к процедурам определения ограничений и генерации решений. Дело в том, что неопределенность в рассматриваемой задаче в процессе выполнения предыдущих процедур существенно сокращается после того, как эксперты проанализировали проблемную ситуацию, сформулировали цели решения проблемы, определили возможный спектр ограничений, выполнили генерацию решений и измерили их предпочтения с точки зрения достижения каждой цели в каждой из рассматриваемых гипотетических ситуаций. Далее необходимо выполнить анализ предпочтений экспертов, обсудить их и на основе этого анализа и обсуждений еще раз сопоставить спектр ограничений и спектр предлагаемых альтернативных решений. Возможно, что при выполнении этой процедуры часть из предлагаемых некоторыми экспертами решений будет отвергнута. Могут быть предложены новые решения или изменена система ограничений, если для этого появились веские основания, такие, как появление новых решений, признаваемых ЛПР или большинством экспертов столь эффективными, что для них окажется необходимым заново выполнить технико–экономические обоснования и откорректировать варианты бизнес–планов.
5.2. Формирование принципов выбора
В СПУР реализовано три принципа группового многокритериального выбора. Первым принципом является принцип Парето [12]. Этот принцип имеет универсальный характер как с точки зрения группового, так и с точки зрения многокритериального выбора. Все множество ранжировок, выполненных каждым экспертом во всех гипотетических ситуациях с точки зрения достижения всех принятых во внимание целей, проверяется с помощью этого принципа. Далее используются критерий Гурвица и принцип медианы, поскольку эти методы дают возможность в большей мере проявить свою компетентность, быть может, субъективную..
5.3. Определение эффективных решений
5.3.1. Описание принципа Парето
Эффективным (оптимальным) по Парето решением считается такое решение, что не существует другого решения, строго лучшего, чем рассматриваемое. При этом «строго лучше» означает «не хуже» по всем показателям и «лучше» хотя бы по одному. С учетом принятых ранее обозначений (раздел 1) решение Yt признается не эффективным и исключается из дальнейшего рассмотрения, если найдется такое решение Ys, доминирующее над Yt, что:
Fmjn(Yt) ≤ Fmjn(Ys)
для всех j, m, n, и если найдется хотя бы одна тройка j0, m0, n0 такая, что:
Fmojono(Yt) < Fmojono(Ys)
В этих соотношениях F обозначает оценку функции предпочтения решения Y, индекс j = 1, 2, …, J – это номер одной из J целей, индекс m = 1, 2, …, M – номер одной из M гипотетических ситуаций, индекс n = 1, 2, … N – номер одного из N экспертов.
Здесь знак ≥ понимается в смысле «не хуже», знак > - «лучше». Для оценок в виде рангов эти соотношения соответственно обозначаются как ≤ и <, поскольку принято, что чем меньше ранг, тем лучше.
Приведем пример, иллюстрирующий метод Парето (рис.5.1) для следующего множества решений Y и соответствующих значений функции предпочтения F. Рассмотрим простейший случай, соответствующий одному эксперту, единственной ситуации, двум целям (G) и четырем альтернативным решениям (Y) (рис. 5.1). Оценки даны в форме рангов. Как видно из рисунка, пара решений Y2 и Y3 удовлетворяет принципу Парето. В самом деле, решения Y2 и Y3 несравнимы между собой, поскольку Y3 по первой цели лучше Y2, а по второй цели Y2 лучше Y3. Далее, для решения Y4, оба оптимальных решения строго лучше. Для решения же Y1 доминирующим по первой цели является решение Y2. Следовательно, решения Y1 и Y4 не являются оптимальными решениями и могут быть исключены из дальнейшего рассмотрения.
F Y |
G1 |
G2 |
Y1 |
3 |
2 |
Y2 |
2 |
1 |
Y3 |
1 |
3 |
Y4 |
4 |
3 |
Y2 несравнимо с Y3
Y2 < Y4; Y3 < Y4
Y2 < Y1 по G1
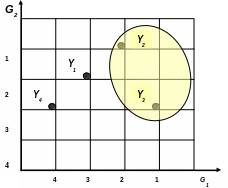
Рис. 5.1. Определение эффективных решений с помощью метода Парето.
Дадим более простую формулировку принципа Парето.
1. Два Парето–оптимальных решения не сравнимы между собой. Парето–оптимальные решения эффективны.
2. Для любого не оптимального по Парето (т.е., не эффективного) решения найдется хотя бы одно оптимальное строго доминирующее решение.
Отметим, что приведенный пример может рассматриваться и с той точки зрения, что обе координаты могут соответствовать не только двум различным целям, но и двум различным экспертам, выразившим свои предпочтения по одной и той же цели. В СПУР принимается, что выбор эффективных решений как раз и осуществляется с помощью принципа Парето.