
- •6.030507 – “Маркетинг”6.030504 – “Економіка підприємства”)
- •Тема 1. Предмет і метод статистики
- •Тема 2. Статистичне спостереження
- •Тема 3. Статистичні зведення і групування
- •Тема 4. Статистичні показники
- •Тема 5. Середні величини та їх види
- •Тема 6. Показники варіації
- •Тема 7. Вибіркове спостереження
- •Повторна вибірка;
- •Безповторна вибірка.
- •Біномінальний розподіл – це дискретний розподіл, який описує розподіл числа появи певної події в послідовності з n – незалежних подій, якщо ймовірність одиничної появи рівна р.
- •Рівномірний розподіл – це дискретний розподіл, який використовується для оцінки рівновеликої появи величини х з певного проміжку.
- •Тема 8. Статистичні методи аналізу взаємозв'язків
- •Тема 9. Ряди динаміки
- •Тема 10. Індекси
- •Статистика:
- •6.0502 „Менеджмент”)
Тема 8. Статистичні методи аналізу взаємозв'язків
Усі явища навколишнього світу, особливо соціально-економічні, взаємопов'язані і взаємообумовлені. Кожне явище є наслідком дії певної множини причин і водночас є причиною для інших явищ. Причини і явища можуть бути пов'язані прямо або опосередковано.
Головна мета вимірювання взаємозв'язків – дати кількісну характеристику причинних зв'язків. Вивчаючи закономірності зв'язку причини та наслідки об'єднують в одне поняття – фактор. Відповідно ознаки, які характеризують фактори, називають факторними. Часто, ті ознаки, які характеризують причини називають незалежними, а ті, що характеризують наслідки, називають результативними.
Розрізняють два типи зв'язків: функціональні та стохастичні.
У разі функціонального зв'язку кожному значенню фактора х відповідає чітко визначене значення (множина значень) y. Наприклад, залежність довжини ртутного стовпчика від температури навколишнього середовища. Знаючи х в кожному випадку точно визначається результат y. На відміну від функціональних стохастичні зв'язки неоднозначні. Наприклад, залежність захворюваності населення від екологічного стану довкілля. На забруднених радіонуклідами територіях, як і на інших стан здоров'я мешканців коливається від тяжко хворого до практично здорового. Хоча в середньому там захворюваність значно вища.
Стохастичні
зв'язки
виявляються як узгодженість варіації
двох чи більше ознак. У зв'язку y=f(x),
кожному значенню х
відповідає множина значень y, яка утворює
так званий умовний
розподіл.
Якщо умовні розподіли замінюються
одним параметром -
![]() ,
то такий зв'язок називається кореляційним.
Наприклад,
при проведенні валютних операцій,
протягом дня, для переведення суми в
національній валюті в еквівалентну їй
суму в іноземній валюті, використовують
валютний курс.
,
то такий зв'язок називається кореляційним.
Наприклад,
при проведенні валютних операцій,
протягом дня, для переведення суми в
національній валюті в еквівалентну їй
суму в іноземній валюті, використовують
валютний курс.
Можна говорити, що аналіз взаємозв'язків полягає не лише у підтвердженні (відхиленні) тверджень про наявність кореляційного зв'язку між факторною ознакою "х" і результативною "y", а й визначенні, як у середньому змінюється "y" в залежності від "х". Ефекти впливу на "y" визначаються відношенням приростів середніх групових цих величин.
Розрізняють такі види зв'язків:
адаптивні (наприклад, а + b + c);
мультиплікативні (наприклад, a b c);
залежності середніх величин від структури сукупності.
Регресійний аналіз.
Важливою характеристикою кореляційного зв'язку є лінія регресії. Наприклад, залежність врожайності від кількості опадів описується параболічною функцією. Емпірична при використанні аналітичного групування і теоретична в моделі регресійного аналізу. Емпірична будується з використанням групових середніх резервної ознаки "y", кожна з яких належить до відповідного інтервалу х. Теоретична лінія регресії описується функцією y = f (x). Наприклад, залежність маси чоловіка до 30 років від росту описується формулою y=x–100.
Різні явища по-різному реагують на зміну факторів. У регресійному аналізі крім звичайного, лінійного зв'язку y = a + bx використовують такі функції:
степеневу y = a b
гіперболічну y = a + b/x
параболічну y = a + b x + с x2
Звичайно є ще й інші форми представлення. При визначенні зв'язку між собівартістю та обігом продукції використовується рівняння регресії.
Метод найменших квадратів
Нехай
задано деякий набір спостережень, які
складаються із впорядкованих пар
![]() .
Ця множина часто представляється у
вигляді таблиці. Ці дані називатимемо
фактичними значеннями. Задача полягає
у побудові кореляційної залежності
між цими величинами x,
y.
.
Ця множина часто представляється у
вигляді таблиці. Ці дані називатимемо
фактичними значеннями. Задача полягає
у побудові кореляційної залежності
між цими величинами x,
y.
Щоб дослідити взаємозв'язок між факторами нанесемо точки на площину x0y. В результаті отримаємо так звану "хмарку", яка містить точки (xi, yi). В залежності від поведінки цієї "хмарки" можна визначити той чи інший вид лінії регресії (параболічний, лінійний, степеневий). Припустимо, що взаємозв'язок лінійний: y = a +bx.
Рівняння регресії шукаємо у вигляді
|
(8.1) |
Лінія
регресії будується таким чином, щоб
відхилення
![]() для будь-якого хі
де
для будь-якого хі
де
![]() розраховується через підстановку хі
в рівняння регресії
розраховується через підстановку хі
в рівняння регресії
![]() ,
а
,
а
![]() - фактичне значення з таблиці. Вимогу,
яка визначає коректність побудови
рівняння регресії описується функціоналом:
- фактичне значення з таблиці. Вимогу,
яка визначає коректність побудови
рівняння регресії описується функціоналом:
|
(8.2) |
Підставимо залежність теоретичного значення у шукане рівняння регресії.
|
(8.3) |
Для того, щоб отримати значення мінімуму функціоналу потрібно задовольнити умовам:
|
(8.4) |
Підставивши (8.1) в (8.3) та виконавши перетворення, отримаємо:
|
(8.5) |
Розкривши дужки, отримаємо:
|
(8.6) |
Звідси можна вивести формули для знаходження a і b.
|
(8.6) |
Дослідження тісноти взаємозв’язку
Дослідимо тісноту взаємозв’язку y від x на основі зібраних статистичних даних. Цю залежність можна характеризувати співвідношенням поясненого до загального відхилення. Загальне відхилення між фактичними та теоретичними значеннями можна представити
|
(8.7) |
Можна аналітично вивести таку залежність:
|
(8.8) |
цю тотожність можна переписати таким чином
|
(8.9) |
Очевидно, що величина першого доданку правої частини вказує на пояснену частку відхилення, а другий – непояснену. Для оцінки тісноти взаємозв’язку використовують такі показники:
|
(8.10) |
|
(8.11) |
З наведених вище формул видно, що величина цих коефіцієнтів лежить в межах [0,1]. Адже R2 характеризує частку поясненого відхилення. Тому чим більша ця частка, тим краще дана економіко-математична модель пояснює сутність досліджуваного взаємозв'язку. За значенням R можна зробити висновки:
R2 0,4 - даний взаємозв'язок не є коректним і йому довіряти не можна;
R2 = 0,4 - 0,6 - довіряти теж не варто, а висновок про наявність взаємозв'язку слід робити після більш детальних досліджень;
R2 0,6 - можна припустити, що взаємозв'язок існує;
R2 0,9 - зв'язок існує і є близький до функціонального;
R у випадку лінійної регресії може бути як додатнім, так і від'ємним. Обернений зв'язок буде, коли R від'ємний, пряма залежність спостерігається при R додатному. При R = 1 - між ознаками існує прямий функціональний зв'язок; а при R = -1 - обернений.
Для лінійної регресії a - точка перетину осі 0y; b - кут нахилу лінії регресії.
На практиці для обчислення коефіцієнта кореляції лінійної регресії зручно використовувати такі формули:
|
(8.12) |
Наприклад, розглянемо залежність ваги людини від її росту. Дані наведені в таблиці
Таблиця 8.
Приклад проведення регресійного аналізу
№ з/п |
xi (ріст, см) |
yi (вага, кг) |
xi2 |
xiyi |
yi2 |
№ з/п |
xi (ріст, см) |
yi (вага, кг) |
xi2 |
xiyi |
yi2 |
1 |
187 |
80 |
34969 |
14960 |
6400 |
12 |
182 |
69 |
33124 |
12558 |
4761 |
2 |
185 |
77 |
34225 |
14245 |
5929 |
13 |
170 |
60 |
28900 |
10200 |
3600 |
3 |
180 |
73 |
32400 |
13140 |
5329 |
14 |
178 |
65 |
31684 |
11570 |
4225 |
4 |
188 |
81 |
35344 |
15228 |
6561 |
15 |
182 |
72 |
33124 |
13104 |
5184 |
5 |
179 |
67 |
32041 |
11993 |
4489 |
16 |
194 |
87 |
37636 |
16878 |
7569 |
6 |
174 |
70 |
30276 |
12180 |
4900 |
17 |
181 |
70 |
32761 |
12670 |
4900 |
7 |
176 |
60 |
30976 |
10560 |
3600 |
18 |
178 |
70 |
31684 |
12460 |
4900 |
8 |
186 |
72 |
34596 |
13392 |
5184 |
19 |
172 |
60 |
29584 |
10320 |
3600 |
9 |
178 |
65 |
31684 |
11570 |
4225 |
20 |
184 |
68 |
33856 |
12512 |
4624 |
10 |
178 |
73 |
31684 |
12994 |
5329 |
21 |
168 |
58 |
28224 |
9744 |
3364 |
11 |
170 |
62 |
28900 |
10540 |
3844 |
|
3770 |
1459 |
677672 |
262818 |
102517 |
Невідомий
розподіл шукаємо у вигляді
![]() .
Для знаходження невідомих параметрів
a i b потрібно розв’язати таку систему
рівнянь
.
Для знаходження невідомих параметрів
a i b потрібно розв’язати таку систему
рівнянь
![]()
Звідси а=-115,43; b= 1,0294 або y=1.0294x-115,43. Графічне зображення наведено на рис. 8.1.

Рис. 6. Лінія регресії
![]()
У невеликих за обсягом сукупностях коефіцієнт регресії b схильний до випадкових коливань, тому його істотність слід перевіряти. У випадку, коли передбачуваний зв'язок лінійний, істотність коефіцієнта регресії перевіряють за допомогою t-критерія Стьюдента. Для гіпотези H0: b=0 визначається відношення коефіцієнта b до власної стандартної похибки в
|
(8.13) |
Тоді
довірчий інтервал для коефіцієнта b
визначається як
![]() .
.
В певних випадках досліджують значущість коефіцієнта кореляції і теж використовується t-критерій Стьюдента, але розраховуємо величину
|
(8.14) |
Теоретичне значення функції розподілу Стьюдента для заданої ймовірності і n-2 ступенів вільності знаходять у таблиці. Якщо tрозр tтабл, тоді гіпотеза про нульове значення коефіцієнта кореляції в генеральній сукупності підтверджується.
Перевірку значущості кореляційного відхилення виконують аналогічно перевірці значущості коефіцієнта кореляції.
При нелінійній кореляції часто застосовують допоміжну оцінку точності наближення, середню відносну похибку апроксимації.
|
(8.15) |
У
випадку дослідження взаємозв'язку між
двома змінними такий аналіз носить
назву однофакторного або парної
регресії. В економіці дуже часто
використовуються нелінійні, наприклад,
степеневі функції
![]() ,
які відображають функції споживання,
виробничі функції. Степенева функція
зводиться шляхом логарифмувань до
лінійного виду
,
які відображають функції споживання,
виробничі функції. Степенева функція
зводиться шляхом логарифмувань до
лінійного виду
.
|
(8.16) |
В реальності часто досліджується взаємозв'язок між багатьма факторами, тобто в такому випадку проводиться множинний аналіз і будується багатофакторне рівняння регресії, яке для лінійного випадку має такий вигляд
|
(8.17) |
Для знаходження невідомих коефіцієнтів b0, b1, … bm використовують метод найменших квадратів.
|
(8.18) |
Прирівнявши частинні похідні по bi до 0 отримуємо систему нормальних рівнянь, з якої знайдемо невідомі коефіцієнти bі.
|
(8.19) |
Коефіцієнт детермінації у випадку багатофакторної регресії за змістом і способом розрахунку ідентичний коефіцієнтам детермінації парної (однофакторної) регресії.
|
(8.20) |
Коефіцієнт еластичності
Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат - коефіцієнт еластичності, який показує на скільки відсотків у середньому змінюється результат y зі зміною фактора х на 1%.
|
(8.21) |
у випадку лінійної регресії коефіцієнт еластичності буде рівним:
|
(8.22) |
Рангова кореляція
Взаємозв'язок між ознаками, які можна проранжувати, передусім на основі простих оцінок, вимірюється методами рангової кореляції.
Рангами називають числа натурального ряду, які згідно з означенням ознаки надаються елементам сукупності і певним чином упорядковують їх порядок. Ранжування проводиться за кожною ознакою окремо. Перший ранг надається найменшому значенню ознаки, останній - найбільшому (можливо й навпаки). Кількість рангів рівна обсягу варіантів сукупностей. Рангова кореляція не потребує додаткових математичних обмежень (наприклад, дотримання нормального розподілу). Ранги, надані елементам сукупності за ознакою х, позначають відповідно Rxi, ранги елементів y - відповідно Ryi.
Таблиця 9
Рангові показники Фехнера і Спірмена.
Коефіцієнт Спірмена |
|
де di = Rxi -Ryi; n - обсяг сукупності; di – різниця рангів. |
(8.23) |
Коефіцієнт Фехнера
|
|
де С - число співпадінь знаку між відхиленнями поточного значення від середнього; Н - число незбіжностей
|
(8.24) |
Коефіцієнти Спірмена та Фехнера лежать в межах від -1 до +1. При = -1 - спостерігається повна зворотна кореляція рангів, при = 0 - кореляція відсутня, при = 1 - повна пряма кореляція рангів.
Непараметричні методи дослідження взаємозв'язків між ознаками
Розглянуті методи вимірювання взаємозв'язків між ознаками прийнято називати параметричними, оскільки вони базуються на використанні середніх величин, дисперсії, які є основними параметрами розподілу. Очевидно, що параметричні методи не можна застосовувати, якщо ознаки не піддаються кількісному виміру або не виконуються припущення про нормальний розподіл ознаки.
Непараметричні методи дослідження служать для виявлення зв'язків між якісними атрибутивними ознаками і не вимагають інформації про розподіл ознак. Ці методи забезпечують лише оцінку щільності зв'язку і перевірку його істотності. В основі обчислення щільності зв'язку між атрибутивними ознаками лежить побутова таблиця взаємоспряжень, в яких представлені комбінаційні розподіли сукупності.
Позначимо через fij число спостережень на перетині і-го рядка і j-го стовпця. У випадку відсутності стохастичної залежності між ознаками, частки умовних розподілів збігаються і дорівнюють часткам безумовного розподілу. Розбіжність між фактичною кількістю спостережень у комбінації таблиці і теоретично можливої за повної відсутності зв'язку знаходять за допомогою показника середньої квадратичної залежності.
|
(8.25) |
При умові відсутності зв'язку між ознаками χ2 = 0.
Таблиця 10
Коефіцієнти взаємного спряження для вимірювання щільності зв'язку між двома ознаками
Коефіцієнт Чупрова |
|
(8.26) |
Коефіцієнт Крамера |
|
(8.27) |
Коефіцієнт Пірсона |
|
(8.28) |
Коефіцієнт Чупрова дає найбільш обережну оцінку зв'язку.
У випадку наявності лише двох альтернативних ознак використовуються спрощені коефіцієнти взаємного спряження:
Таблиця 11
Спрощені коефіцієнти взаємного спряження
1) коефіцієнт контингенції |
|
(8.29) |
2) коефіцієнт асоціації
|
|
(8.30) |
Наприклад, потрібно проаналізувати рівень довіри до таких зібраних даних
Таблиця 12
Дані опитування населення
Населення |
Підтримує політику уряду |
Не підтримує політику уряду |
Всього |
Міське |
500 |
500 |
1000 |
Сільське |
300 |
700 |
1000 |
Всього |
800 |
1200 |
2000 |
Коефіцієнт
контингенції
![]()
Коефіцієнт
асоціації
![]() =0,40
=0,40

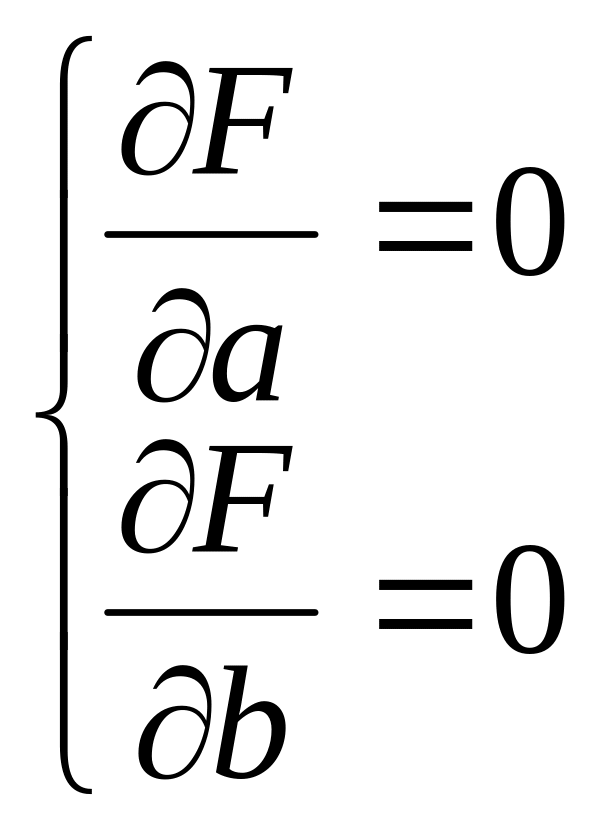 .
. .
. .
. ,
,
 .
. .
. .
. .
. .
. .
. .
.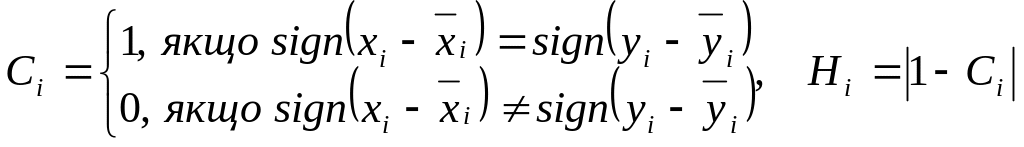
 ,
де
,
де
