Перевод чисел из одной системы счисления в другую

Основанием восьмиричной и шестнадцатиричничной систем счисления является целая степень числа 2. Например: 8 = 2³ // 16 = 2⁴ Этим объяняется простота преобразования чисел представленных в этих системах, в двоичную систему счисления и обратно. Для перевода чисел из восьмиричной системы счисления в двоичную надо каждую цыфру восьмиричного числа представить трёх разрядным двоичным числом. Например: 762, 35₈  2 762, 35₈  111 110 010, 011 101₂ 7 6 2 , 3 5 Перевод в 16-ричную в 2-ую достигается представлением цыфр шеснадцатиричного числа четырёх разрядными двоичными числами. Пример: А7В,С7₁₆ 2 // А7В,С7₁₆ = 1010 0111 1011 , 1100 0111­₂

А 7 В , С 7

При обратном переводе чисел из двоичной системы в восмеричную или в шестнадцатиричную системы счисления надо разряды двоичного числа отчитывая от запятой влево и вправо, разбить на группы по три разряда в случаи перевода в восьмиричную систему или на группы по четыре разряда в случае перевода в шестнадцатиричную систему. Неполные крайние группы дополняются нулями, затем каждая двоичная группа представляется цыфрой той системы счисления в которую переводится число. Например: 8=2³ 001111, 101010  8 1 7 , 5 2 То есть получается 001111, 101010 = 17, 52­₈

Еще пример: 16=2⁴ 01011100, 11010110 – 16 5 12=C 13=D 6

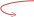То есть получается 01011100, 11010110 = 5C,D6₁₆

02.02.2012

• Позиционный способ 9 А 5 F , C 8 3 B₁₆  10 9*16³+ 10*16²+ 5*16¹ + 15*16⁰ + 12*16^-1 + 8*16^-2 + 3*16^-3 + 11*16^-4 = 36864 + 2560 + 80 + 15 + 0,75 + 0.03125 + 0.000732421 + 0.000167846= 39519, 7821502₁₀

• 39519₁₀  16

• Из десятичной в двоичную

21₁₀  2

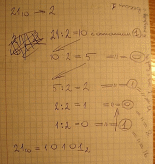
• 0, 7821502₁₀  16

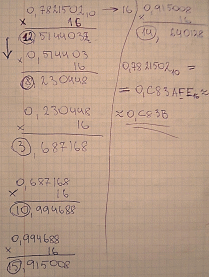
07.02.2012

Пример:

47₁₀  16 47/16 = 2 с остатком 15 в разряд с весом 1

2/16 = 0 с остатком 2 в разряд с весом 16

Ответ: 47₁₀ = 2F_16­

Арифмитические операции в двоичной системе счисления

• Основной операцией, которая используются в цифровых устройствах при выполнении различных арифметических действий является алгебраическое сложение (сложение в котором могут участвовать как положительные так и отрицательные числа) .

• Вычитание сводится к сложению путём изменения знака вычитаемого на обратный.

  

• При записи числа будем знак числа представлять заключаемыми в кружки цифрами 0 – для положительного числа, а 1 – для отрицательного числа.

Пример сложения:

1+1=10 (двоичная система)

• Цифры разрядов суммы формируются начиная с младшего разряда.

Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде Р>= 2 (P-основание системы счисления). При этом в разряд суммы записывается цифра на Р единиц меньшая результата суммирования.

Алгебраическое сложение с использованием дополнительного кода.

В двоичной системе дополнительный код отрицательного числа формируется по следующему правилу: инвертируются ( путём замены 0 на 1, 1 на 0 ) цифры всех разрядов ,кроме знакого, после чего в младший разряд прибавляется 1. Перенос возникающей из знакого разряда отбрасывается.

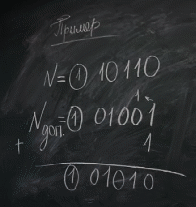
Пример:

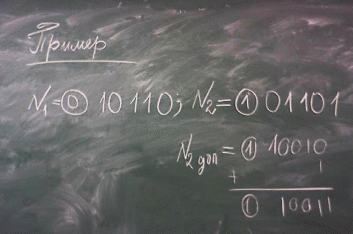
Пример:

Пример:

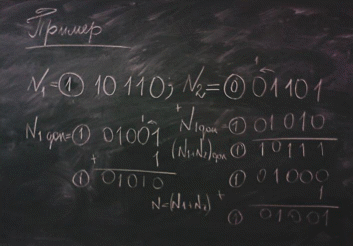
Если результат сложения есть отрицательное число,то оно оказывается представленным в дополнительном коде.Число надо преобразовать из дополнительного кода в прямой по тому же правилу.

09.02.2012