2. Работа расширения газа

2.2.1. В вертикально расположенном цилиндре под поршнем массой m = 10 кг и площадью s = 110 ^{­ 2} м находится воздух. При изобарном нагревании поршень поднимается на высоту h = 0,2 м. Какая работа, при этом, совершена воздухом? Атмосферное давление постоянно и равно p₀ = 0,1 МПа.

Решение

1. Работа в данном случае будет складываться из работы преодоления атмосферного давления и работы, затрачиваемой на перемещение поршня.

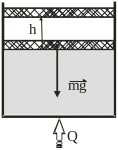
2. При расширении газа на поршень будет со стороны газа действовать сила F = p₀s, работа которой определится как: A₁ = p₀sh.

3. Работа по перемещению поршня численно будет равна изменению его потенциальной энергии A₂ = mgh.

4. Полная работа рассматриваемого процесса, таким образом, будет представляться следующим соотношением

. (1)

2.2.2. Какую работу совершает газ в количестве  = 12 моль при изобарном увеличении его температуры с t₁ = 0 ⁰C до t₂ = 100 ⁰C?

Решение

1. Запишем уравнение Клапейрона ­ Менделеева

, (1)

и проанализируем размерность комбинации величин pV

. (2)

Как видно, левая часть уравнения Клапейрона ­ Менделеева имеет размерность энергии или работы, что позволяет уравнение (1) переписать следующим образом

. (3)

2.2.3. Какую работу совершает кислород массой m = 0,32 кг при изобарном нагревании на Т = 20 К?

Решение

1. На основании анализа, проведенного в предыдущей задаче, уравнение Клапейрона ­ Менделеева можно записать так

. (1)

2. Подставим заданные величины в последнее соотношение, с учётом того, что молярная масса  = 3210 ^{­ 3} кг/моль

. (2)

2.2.4. Какая масса водорода находится в цилиндре под поршнем, если при изменении температуры на T = 430 К совершается работа А = 400 Дж?

Решение

1. Разрешим уравнение (1) предыдущей задачи относительно искомой массы

. (1)

2.2.5. Газ, занимающий объём V₁ = 12 л под давлением p₁ = 0,1 МПа, был изобарно нагрет от температуры от температуры Т₁ = 300 К до температуры Т₂ = 400 К. Определить работу расширения газа.

Решение

1. Запишем систему уравнений для двух анализируемых состояний газа с целью определения величины конечного объёма

. (1)

2. Найдём далее работу расширения газа

. (2)

2.2.6. Кислород массой m = 0,16 кг, находящийся при начальной температуре t₀ = 27 ⁰C под действием внешней силы уменьшил свой объём в пять раз. Определить работу внешней силы.

Решение

1. Заданный процесс изменения состояния происходит при постоянной температуре, т.е. изотермически. Работа при изотермическом процессе определяется уравнением

. (1)

2. Применительно к заданным условиям, уравнение (1) можно переписать в виде

. (2)

2.2.7. В вертикальном цилиндре с площадью основания s = 10 ^{­ 2} м² находится газ при температуре Т₁ = 300 К. На расстоянии h = 0,25 м от основания расположен лёгкий поршень, на который поставлена гиря массой m = 2 кг. Какую работу совершит газ при его нагревании на Т = 100 К? Атмосферное давление равно р₀ = 0,1 МПа.

Решение

1. Определим начальный объём, занимаемый газом

. (2)

2. Найдём изменение объёма при нагревании газа

. (3)

3. При нагревании газа будет совершаться работа по преодолению силы тяжести поршня и силы, вызванной действием атмосферного давления

(3)

. (4)

2.2.8. В цилиндре под поршнем при температуре Т₁ = 300 К и давлении р₁ = 0,2 МПа находится водород, занимающий объём V₁ = 810 ^­4 м³. Как изменится температура газа, если изобарно над ним произвести работу А = 50 Дж?

Решение

1. На основании уравнения изобарного процесса определим изменение объёма газа при совершении заданной работы

. (1)

2. Запишем далее уравнение работы при изобарном процессе

. (2)

3. Определим из уравнения (2) искомое изменение температуры

(3)

4. При совершении заданной работы температура газа уменьшится на 9,4 К.

2.2.9. При изобарном нагревании газа от t₁ = 20 ⁰C до t₂ = 50 ⁰C совершается работа А = 2500 Дж. Определить число молекул, участвующих в процессе.

Решение

1. Запишем уравнение (1) задачи 2.2.3 в следующем виде

. (1)

2. Произведём замену комбинации величин , т.е. заменим комбинацию универсальной газовой постоянной R и числа Авогадро N_A на постоянную Больцмана k_B.

. (2)

2.2.10. Найти работу изотермического расширения двух молей идеального одноатомного газа, если известно, что концентрация молекул в конечном состоянии в два раза меньше, чем в начальном состоянии при температуре Т₁ = 300 К.

Решение

1. Работу при изотермическом расширении газа определим, исходя из уравнения

. (1)

2. Концентрация молекул определяется как: , другими словами, при неизменности числа частиц уменьшение концентрации молекул в два раза, сопровождается увеличением объёма в два раза. Уравнение (1) в этой связи можно переписать так

. (2)

2.2.11. В двух идентичных цилиндрах под одинаковыми поршнями находятся в равных количествах и равнозначных условиях водород и кислород. Сравнить работы, которые совершают эти газы при изобарном нагревании. Массы, начальные и конечные температуры газов одинаковы.

Решение

1. При изобарном нагревании работа в общем случае определяется уравнением

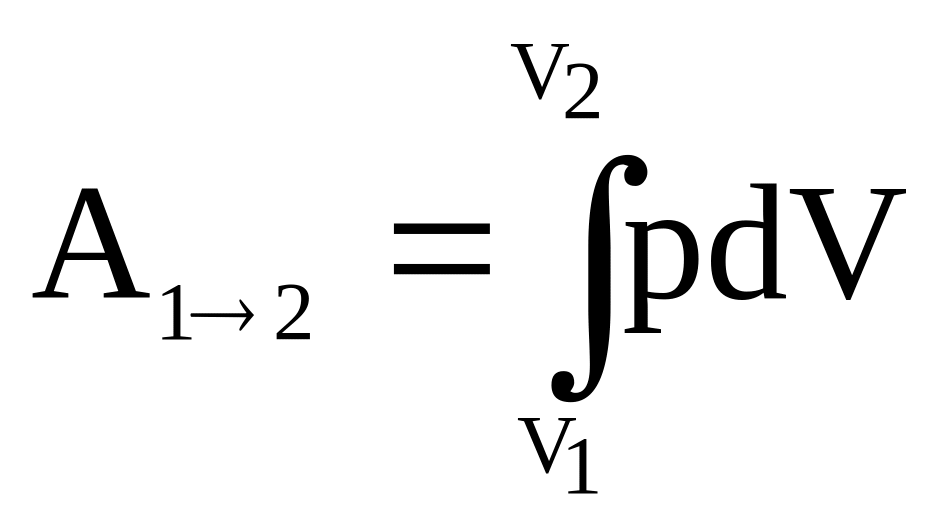, (1)

при линейном изменении температуры

. (2)

2. По условию задачи величина Т и m для сравниваемых газов одинаковы, поэтому отношение работ представится следующим образом

. (3)

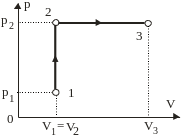
2.2.12. Некоторая масса газа, занимающего объём V₁ = 0,01 м³, находится под давлением р₁ = 0,1 МПа при температуре Т₁ = 300 К. Газ вначале нагревают при постоянном объёме до температуры Т₂ = 320 К, а затем при постоянном давлении доводят температуру до Т₃ = 350 К. Найти работу газа при переходе из состояния 1 в состояние 3.

Решение

1. Переход газа из состояния 1 в состояние 2 не будет сопровождаться совершением работы, вся подводимая от внешнего источника энергия будет увеличивать внутреннюю энергию газа.

2. На участке 2 ­ 3, который протекает по изобарной схеме, совершается работа, определяемая уравнением

. (2)

3. Определим величину давления р₂, используя уравнение изохорного процесса

. (3)

4. Найдём далее конечный объём газа

. (4)

5. Подставим р₂ и V₃ в уравнение (2)

. (5)

2.2.12. Некоторый газ переводится из начального состояния 1 в конечное состояние 4, как показано на рисунке. Какая при этом совершается газом работа?

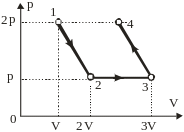
Решение

1. На участках 1 ­ 2 и 3 ­ 4 совершается одинаковая по величине, обратная по знаку работа. На участке 1 ­ 2 газ расширяется, а на участке 3 ­ 4 происходит эквивалентное по объёму сжатие, другими словами,

. (1)

2. Изменение состояния на участке 2 ­ 3 происходит при постоянном давлении, причём объём газа изменяется от V до 2V, т.е. V = V

. (2)

2.2.13. Водород массой m = 510 ^{­ 3} кг при постоянной температуре Т = 290 К изменяет свой объём в три раза. Определить совершаемую при этом работу.

Решение

1. Процесс изменения состояния газа изотермический, работа такого процесса определяется уравнением

. (1)

2. Применительно к условиям данной задачи уравнение (1) можно переписать следующим образом

. (2)

2.2.14. При адиабатном сжатии кислорода массой m = 1 кг совершается работа А = 0,1 МДж. Определить конечную температуру процесса, если он начался при температуре Т₁ = 300 К.

Решение

1. При адиабатном процессе, когда отсутствует теплообмен с внешней средой, т.е. Q = 0, работа определяется следующим образом

(1)

2. Молекула кислорода состоит из двух атомов, поэтому имеет пять степеней свободы i = 5, молярная масса кислорода равна  = 3210 ^{­ 3} кг/моль. Уравнение теплоёмкости кислорода при неизменном объёме представится следующим образом

. (2)

3. Подставим значение удельной теплоёмкости c_V в уравнение (1)

. (3)

4. Выразим из уравнения (3) разность температур

. (4)

5. Конечная температура, таким образом, равна Т₁ + Т  454 К.

2.2.15. Определить работу адиабатного расширения водорода массой m = 410 ^{­ 3} кг, если температура газа понизилась на Т = 10 К.

Решение

1. Воспользуемся для решения задачи уравнением (3) предыдущей задачи, с учётом того что число степеней свободы двухатомной молекулы водорода i = 5, молярная масса ­  = 210 ^{­ 3} кг/моль

. (1)

2.2.16. Азот массой m = 210 ^­3 кг при температуре Т₁ = 300 К адиабатно сжат так, что его объём уменьшился в n = 10 раз. Определить конечную температуру азота Т₂ и работу сжатия А.

Решение

1. Для определения конечной температуры воспользуемся уравнением взаимосвязи между конечными и начальными параметрами состояния газа при адиабатном процессе

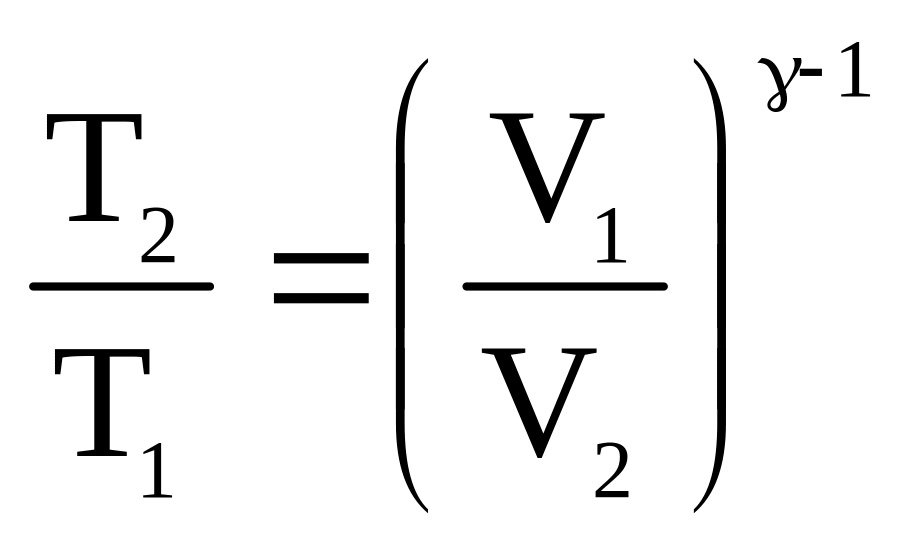. (1)

2. Определим показатель адиабаты с учётом того, что двухатомная молекула азота имеет пять степеней свободы i = 5

. (2)

3. Перепишем уравнение (1) с учётом условий задачи

. (3)

4. Работу сжатия найдём по уравнению (1) предыдущей задачи

. (4)

2.2.17. Кислород массой m = 1 кг, находящийся при температуре Т₁ = 300 К уменьшил адиабатно свой объём в n = 10 раз. Определить работу процесса.

Решение

1. Определим показатель адиабаты кислорода

. (1)

2. Работа процесса, при этом, будет равна

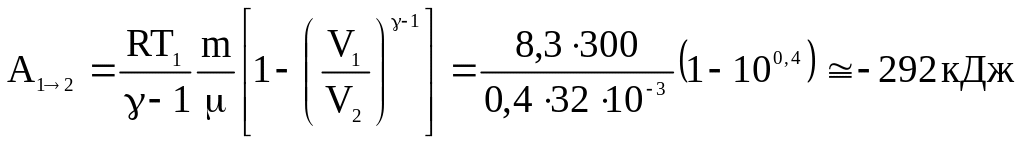. (2)

Отрицательный знак показывает, что процесс протекает с потреблением энергии, подводимой от внешнего источника.

143