Лекція №7 розрахунок надійності послідовно-паралельних структур (частина 1)

1. Метод еквівалентування.

Даний метод базується на використанні залежностей для відшукання імовірностей безвідмовної роботи та відмови системи:

- при послідовному з′єднанні елементів

, , (7.1)

- при паралельному з′єднанні елементів

, , (7.2)

де - імовірність безвідмовної роботи і-го елемента; - імовірність відмови і-го елемента.

Р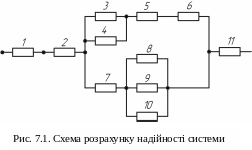 озглянемо використання даного метода на прикладі схеми, що наведена на рис. 7.1.

Позначимо:

; ;

; .

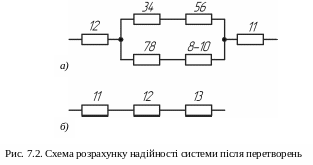
Тоді схема приймає вигляд, як показано на рис. 7.2, а.

Для останньої схеми позначимо:

; ; .

З урахуванням останніх позначень схема наведена рис. 7.2, б.

Імовірностей безвідмовної роботи системи становить:

.

2. Метод взаємної заміни «трикутника» та «зірки».

2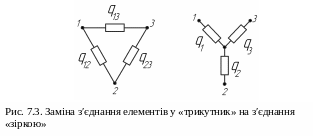 .1. Заміна «трикутника» на «зірку». Припустимо, що необхідно заміна з′єднання елементів у «трикутник» на з′єднання «зіркою» (рис. 7.3). При цьому така трансформація не має змінити надійності кіл 1-2, 1-3, 2-3.

Розглянемо коло 1-3 «трикутника». Позначимо - імовірність безвідмовної роботи послідовного з′єднання елементів та :

; (7.3)

. (7.4)

Тоді імовірність відмови кола 1-3 «трикутника» становить:

. (7.5)

Для кіл 1-2 та 2-3 «трикутника» аналогічно отримаємо:

; (7.6)

. (7.7)

Імовірність відмови кола 1-3 «зірки» (рис. 7.3) становить:

. (7.8)

Для кіл 1-2 та 2-3 «зірки» (рис. 7.3) маємо:

; (7.9)

. (7.10)

Надійність кіл «трикутника» та «зірки» має бути однаковою, тобто має виконуватися умова:

(7.11)

З урахуванням залежностей (7.5)-(7.10) умова (7.11) має вигляд:

(7.12)

Нехтуючи в лівій частині виразів (7.12) добутками , а в правій – добутками виду , маємо:

(7.13)

Для того, щоб отримати залежності параметрів елементів «зірки» від «трикутника», необхідно виконати алгебраїчне складання рівнянь системи (7.13) за наступною схемою:

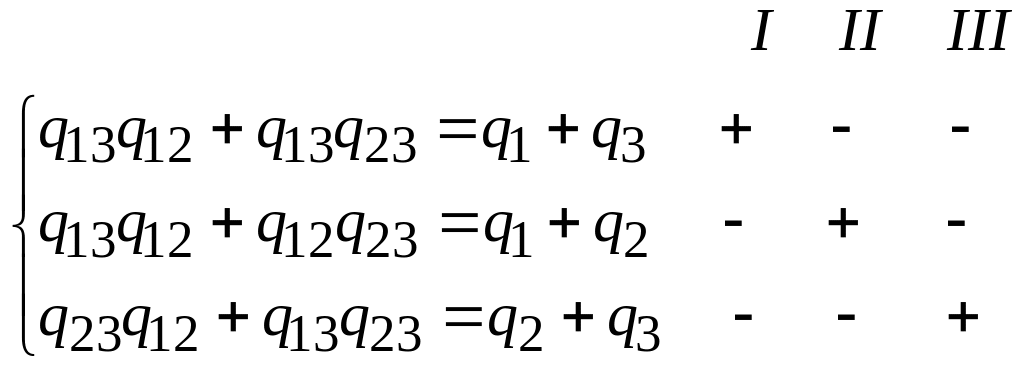(7.14)

При використанні знаків згідно I отримаємо: . Аналогічно отримаємо вирази для та .

Таким чином, для заміни з′єднання елементів у «трикутник» на з′єднання «зіркою» необхідно скористатися виразами:

(7.15)

2.1. Заміна «зірки» на «трикутник». При необхідності перетворити з′єднання елементів «зіркою» на з′єднання у «трикутник» має бути виконане множення та ділення рівнянь системи (7.15) за наступною схемою:

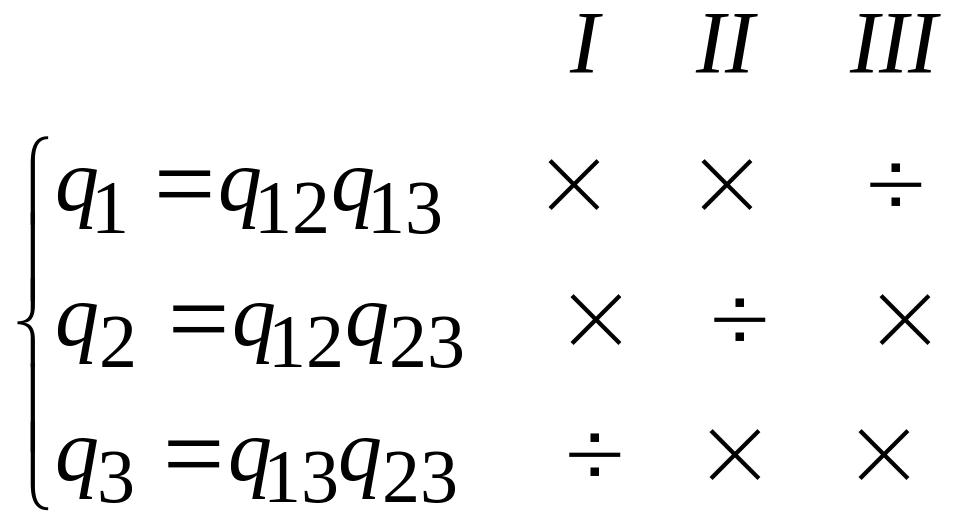(7.16)

При використанні знаків згідно I отримаємо:

, (7.17)

звідки маємо:

. (7.18)

При використанні знаків згідно II та III отримаємо відповідно:

; (7.19)

. (7.20)

3. Метод базового елемента.

Метод базується на використанні теореми про суму імовірностей несумісних подій, яка формулюється наступним чином: імовірність виникнення однієї з двох несумісних подій (не має значення якої) дорівнює сумі імовірностей даних подій:

. (7.21)

При використанні даного метода у складній структурі обирають базовий елемент і приймають два припущення, відповідно до яких перетворюють схему.

Припущення №1. Базовий елемент є абсолютно надійним, тобто завжди знаходить ся у працездатному стані. Таке припущення дозволяє замінити базовий елемент перемичкою, а сам базовий елемент послідовно підключити до отриманої структури з заданим значенням імовірності безвідмовної роботи. Для модифікованої таким чином схеми згідно методу еквівалентування обраховуються імовірність безвідмовної роботи.

Припущення №2. Базовий елемент є абсолютно ненадійним, тобто завжди знаходить у непрацездатному стані. Замість базового елемента в схемі залишають розрив, а його підключають послідовно к структурі з урахуванням його імовірності відмови. Для модифікованої таким чином схеми згідно методу еквівалентування обраховуються імовірність безвідмовної роботи.

Імовірність безвідмовної роботи системи визначається залежністю:

. (7.22)