3. Вынужденные колебания точки с учетом сопротивления движению.

Рассмотрим влияние сопротивления движению на вынужденные колебания материальной точки, полагая модуль силы сопротивления пропорциональным первой степени скорости точки. Рассмотрим материальную точку М (рис. 4.7), совершающую прямолинейное движение под действием восстанавливающей силы , возмущающей силы , изменяющейся по гармоническому закону, и силы сопротивления . Направим ось х по траектории точки М, поместив начало координат О в положение покоя точки, соответствующее недеформированной пружине.

Определим проекции сил , и на ось х в момент времени t, когда движущаяся точка М имеет координату х. Проекция восстанавливающей силы , направленной к положению покоя О, определится формулой

.

Проекция возмущающей силы , изменяющейся по гармоническому закону, определяется формулой (4.1):

Проекция силы сопротивления , направленной противоположно скорости и ей пропорциональной, определяется формулой:

Дифференциальное уравнение движения точки под действием сил , , имеет вид

Перенеся члены сх и в левую часть равенства и разделив уравнение на m, получаем

Рассмотрим коэффициенты уравнения. Здесь с/т=k² - квадрат частоты свободных колебаний: α/m= 2n, где n - коэффициент затухания, Н/т = h - отношение амплитуды возмущающей cилы к массе точки.

При этих обозначениях дифференциальное уравнение движения точки имеет вид

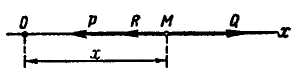
Рис. 4.7

. (4.22)

Уравнение (4.22) представляет собой дифференциальное уравнение вынужденных колебаний при наличии сопротивления движению, пропорционального скорости.

Общее решение уравнения (4.22) состоит из общего решения ypaвнения и частного решения данного уравнения (4.22):

х=х* + х**.

Общее решение уравнения х* в зависимости от соотношения величин k и n может иметь вид (3.4), (4.2) или (4.3). Частное решение уравнения (4.22) имеет вид

. (4.23)

Постоянные и ε должны быть определены подстановкой функции х** и ее производных в уравнение (4.22). Для этого найдем ** и **:

.

Подставим х**, **, ** в уравнение (4.22):

. (a)

Преобразуем правую часть этого равенства:

Подставим это выражение в правую часть равенства (а), перенесем все члены в левую часть и сгруппируем отдельно члены, содержащие sin(pt + δ - ε) и cos (pt + δ - ε):

.

Это равенство справедливо при всех значениях аргумента (pt+δ-ε) лишь при равенстве нулю коэффициентов при sin(pt+δ-ε) и при cos (pt+δ-ε). Приравниваем эти коэффициенты нулю:

. (4.24)

Из выражений (4.24) определяем значения А_с и ε:

(4.25)

(4.26)

(4.27)

(4.28)

Так как sin ε>0, то 0<ε<π.

Подставляя найденное значение А_с и учитывая, что величина ε тоже найдена, получаем частное решение уравнения (4.22 ) в виде

(4.29)

Общее решение уравнения (4.22) в зависимости от соотношения величин k и n имеет вид:

1) при n<k

(4.30)

2) при n > k

(4.31)

3) при n= k

(4.32)

Величины A и β в уравнениях (4.30) и (4.31), а также С₁ и С₂ в уравнении (4.32) являются постоянными интегрирования и определяются по начальным условиям движения.

Движение материальной точки под действием восстанавливающей и возмущающей сил и силы сопротивления среды, пропорциональной: скорости точки, представляет собой наложение собственно вынужденных колебаний на затухающие колебания при n<k или наложение вынужденных колебаний на апериодическое движение при n≥k. Наличие множителя в членах, соответствующих затухающим колебаниям или апериодическому движению, обусловливает быстрое затухание этих движений. Поэтому при установившемся режиме, т. е. через достаточно большой промежуток времени после начала движения, результирующее движение точки практически состоит только из собственно вынужденных колебаний, определяемых уравнением (4.29):

.

На рис. 4.8 показан график движения точки в случае n< k.

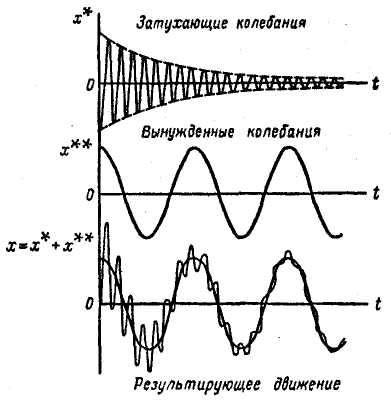
Рис. 4.8

Исследование вынужденных колебаний при наличии сопротивления движению. Уравнение (4.29) показывает, что вынужденные колебания материальной точки при сопротивлении среды, пропорциональном скорости точки, являются гармоническими колебаниями, так как амплитуда их не изменяется с течением времени, т. е. вынужденные колебания под влиянием сопротивления не затухают. Они не затухают потому, что возмущающая сила все время поддерживает колебательное движение точки.

Этим вынужденные колебания существенно отличаются от свободных колебаний, которые затухают даже при самом незначительном сопротивлении.

Частота и период вынужденных колебаний. Частота р и период τ=2π/р вынужденных колебаний точки при наличии сопротивления равны частоте и периоду изменения возмущающей силы, т. е. сопротивление не влияет на частоту и период вынужденных колебаний.

Фаза вынужденных колебаний. Фаза вынужденных колебаний точки при наличии сопротивления (рt+δ-ε) отстает от фазы возмущающей силы (pt+δ) на величину ε, называемую сдвигом фазы и определяемую формулами (4.5).

Из формулы (4.27) следует, что 0<ε<π. В этих пределах сдвиг фазы ε однозначно определяется формулой (4.26):

или .

Величина ε зависит от отношения p/k, характеризующего возмущающую силу, и от отношения n/k, характеризующего сопротивление среды. Поэтому, задавшись определенным значением отношения n/k, можно построить кривую зависимости ε от отношения p/k. Такие кривые построены на рис. 4.9 для различных значений n/k.

При отсутствии сопротивления n=0 и tg ε=0. B этом случае ε=0 для вынужденных колебаний малой частоты (р < k) и ε=π для вынужденных колебаний большой частоты (р > k).

Под влиянием сопротивления этот разрыв сглаживается.

Если р= k, то при любом значении коэффициента затухания n

, т. е. .

Зная k, р и п, можно определить сдвиг фазы непосредственно по графику.

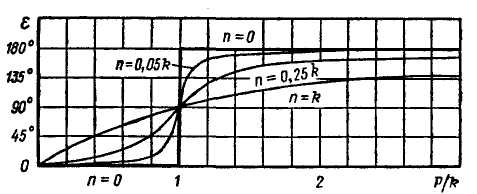
Рис. 4. 9

Амплитуда вынужденных колебаний. Амплитуда вынужденных колебаний точки при наличии сопротивления определяется по формуле (4.25). Из этой формулы следует, что большему сопротивлению среды, т.е. большему значению коэффициента затухания n, соответствует меньшая амплитуда вынужденных колебаний А_с.

Для установления зависимости амплитуды вынужденных колебаний А_с от частоты изменения возмущающей силы р воспользуемся коэффициентом динамичности η. Этот коэффициент представляет собой отношение амплитуды вынужденных колебаний под действием возмущающей силы модуль которой Q=|H sin (pt +δ)|, к статическому отклонению точки от начала координат A₀ = h/k² под действием постоянной силы :

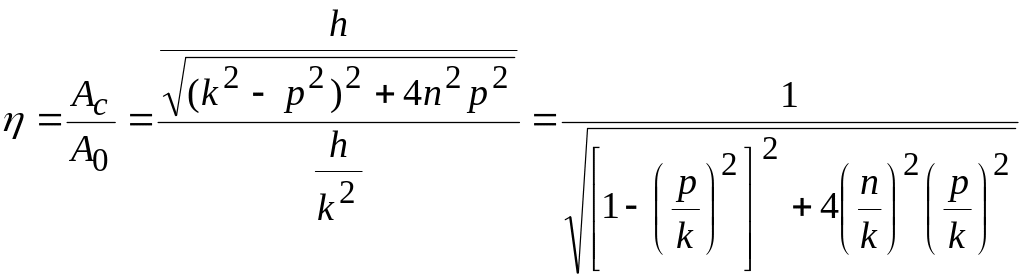. (4.33)

Так как коэффициент динамичности зависит от p/k и n/k то на рис. 4.10 построены кривые, каждая из которых представляет собой зависимость η от p/k при определенном значении n/k.

При отсутствии сопротивления явление резонанса выражается в стремлении амплитуды вынужденных колебаний к бесконечности. Выше на рис. 4.10 кривая, соответствующая п=0, имеет разрыв при р=k, т. е. при p/k = 1. При наличии сопротивления амплитуда, определенная по формуле (4.25), при р = k имеет конечную величину

. (4.34)

Найдем по правилам дифференциального исчисления то значение р, при котором A_c имеет максимум, а следовательно, подкоренное выражение знаменателя в (4.25) имеет минимум. Для этого найдем производную этого выражения по р и приравняем ее нулю:

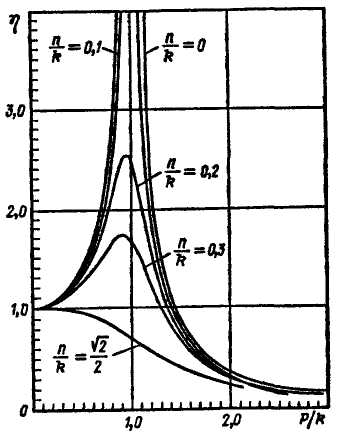
Рис. 4.10