Уравнение Бернулли.

Определение. Уравнением Бернулли называется уравнение вида

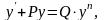
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

Для этого разделим исходное уравнение на yⁿ.

Применим подстановку, учтя, что .

Т.е. получилось линейное уравнение относительно неизвестной функции z.

Решение этого уравнения будем искать в виде:

Пример 10. Решить уравнение

Решение. Разделим уравнение на xy²:

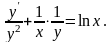
Полагаем .

Полагаем

Произведя обратную подстановку, получаем:

Пример 11. Решить уравнение

Решение. Разделим обе части уравнения на

Полагаем

Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:

Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:

Получаем:

Применяя обратную подстановку, получаем окончательный ответ:

_Пример 12. Решить уравнение

Решение. Разделив обе части уравнения на x²y²: , убеждаемся что это уравнение Бернулли, где

_Заменяя функцию , имеем

Подставляя в исходное уравнение, получаем:

_или

Т.к. одну из вспомогательных функций можно взять произвольно, то выберем в качестве v какой-либо частный интеграл уравнения

Разделяя переменные и интегрируя, получим:

Для нахождения второй неизвестной функции u подставим поученное выражение для функции v в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

Тогда для отыскания u получим уравнение

Подставляя v, найдём u как общий интеграл уравнения:

Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

Подставляя полученные значения, получаем общий интеграл данного уравнения:

Пример 13. Решить уравнение

Решение. Преобразовав данное уравнение к виду

или

Выясняем, что оно является линейным, если рассматривать х как функцию от у.

Далее заменяя функцию х по формуле x=uv, где u и v функции от у, имеем

или

Т.к. одну из вспомогательных функций можно взять произвольно, то выберем в качестве v какой-либо частный интеграл уравнения

Разделяя переменные и интегрируя, получим:

Для нахождения второй неизвестной функции u подставим поученное выражение для функции v в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

Подставляя v, найдём u как общий интеграл уравнения:

Второй интеграл находится по формуле интегрирования по частям

Следовательно,

Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию. Подставляя полученные значения, получаем общий интеграл данного уравнения:

Подставляя сюда заданные значения переменных , _{у = 1} находим значение произвольной постоянной

Следовательно, искомый частный интеграл будет