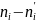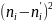- •Содержание
- •Начальный и центральный теоретические моменты.
- •Обычные, начальные и центральные эмпирические моменты.
- •Условные эмпирические моменты. Отыскание центральных моментов по условным.
- •Метод моментов для точечной оценки параметров распределения.
- •Примеры решения задач.
- •Практическая часть. Задача 1.
- •Решение:
- •Задача 2.
- •Решение:
- •Список использованной литературы.
Примеры решения задач.
Пример
1. Найти
методом моментов по выборке
,
,
…,
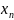 точечную оценку неизвестного параметра
точечную оценку неизвестного параметра
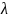 показательного распределения, плотность
распределения которого
показательного распределения, плотность
распределения которого
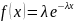 (x
(x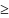 0).
0).
Решение. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: .
Учитывая, что = ,
получим ,
Приняв во внимание, что математическое ожидание показательного распределения равно 1/ , имеем
1/ = .
Отсюда
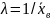 .
.
Итак, искомая точечная оценка параметра показательного распределения равна величине, обратной выборочной средней:
 .
.
Пример
2. Найти
методом моментов по выборке
,
,
…,
точечные оценки неизвестных параметров
а и
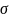 нормального распределения
нормального распределения
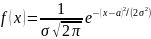 .
.
Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а так же центральные и эмпирические моменты второго порядка:
, = .
Учитывая, что = , = , = , получим
,
= .
Приняв во внимание,
что математическое ожидание нормального
распределения равно параметру а,
дисперсия равна
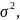 имеем:
имеем:
а =
,
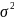 =
.
=
.
Итак, искомые точечные оценки параметров нормального распределения:
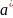 =
,
=
,
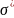 =
=
 .
.
Практическая часть. Задача 1.
Условие: Даны экспериментальные данные, записанные в виде статистического ряда.
Требуется: 1) записать значения результатов эксперимента в виде вариационного ряда;
2) найти размах варьирования и разбить его на 9 интервалов;
3) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
4) Найти числовые характеристики выборки.
76 |
28 |
151 |
91 |
60 |
204 |
177 |
102 |
128 |
217 |
120 |
66 |
207 |
126 |
124 |
152 |
27 |
221 |
131 |
51 |
241 |
77 |
250 |
134 |
123 |
147 |
184 |
195 |
47 |
160 |
159 |
74 |
169 |
178 |
79 |
129 |
250 |
223 |
182 |
96 |
135 |
199 |
56 |
25 |
82 |
116 |
44 |
229 |
145 |
203 |
88 |
209 |
146 |
224 |
239 |
103 |
201 |
245 |
130 |
163 |
71 |
165 |
176 |
194 |
78 |
154 |
99 |
78 |
127 |
69 |
171 |
173 |
31 |
181 |
117 |
84 |
73 |
161 |
240 |
149 |
247 |
107 |
140 |
53 |
205 |
155 |
29 |
132 |
185 |
179 |
180 |
128 |
42 |
114 |
93 |
191 |
174 |
210 |
133 |
226 |
Решение:
а) запишем значения результата эксперимента в вариационный ряд, таблица 1:
25 |
27 |
28 |
29 |
31 |
42 |
44 |
47 |
51 |
53 |
56 |
60 |
66 |
69 |
71 |
73 |
74 |
76 |
77 |
78 |
78 |
79 |
82 |
84 |
88 |
91 |
93 |
96 |
99 |
102 |
103 |
107 |
114 |
116 |
117 |
120 |
123 |
124 |
126 |
127 |
128 |
128 |
129 |
130 |
131 |
132 |
133 |
134 |
135 |
140 |
145 |
146 |
147 |
149 |
151 |
152 |
154 |
155 |
159 |
160 |
161 |
163 |
165 |
169 |
171 |
173 |
174 |
176 |
177 |
178 |
179 |
180 |
181 |
182 |
184 |
185 |
191 |
194 |
195 |
199 |
201 |
203 |
204 |
205 |
207 |
209 |
210 |
217 |
221 |
223 |
224 |
226 |
229 |
239 |
240 |
241 |
245 |
247 |
250 |
250 |
б) находим размах варьирования:
R
=
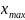 -
-
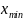 = 250 – 25 = 225
= 250 – 25 = 225
Находим длину интервала:
h
=
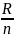 =
=
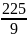 = 25
= 25
Составим таблицу 2:
Номер интервала |
Граница интервала |
Середина интервала
|
Частота |
Относительная
частота
|
Плотность
относительной частоты
|
1 |
[25;50) |
37,5 |
8 |
0,08 |
0,0032 |
2 |
[50;75) |
62,5 |
9 |
0,09 |
0,0036 |
3 |
[75;100) |
87,5 |
12 |
0,12 |
0,0048 |
4 |
[100;125) |
112,5 |
9 |
0,09 |
0,0036 |
5 |
[125;150) |
137,5 |
16 |
0,16 |
0,0064 |
6 |
[150;175) |
162,5 |
13 |
0,13 |
0,0052 |
7 |
[175;200) |
187,5 |
13 |
0,13 |
0,0052 |
8 |
[200;225) |
212,5 |
11 |
0,11 |
0,0044 |
9 |
[225;250] |
237,5 |
9 |
0,09 |
0,0036 |
в) строим полигон частот
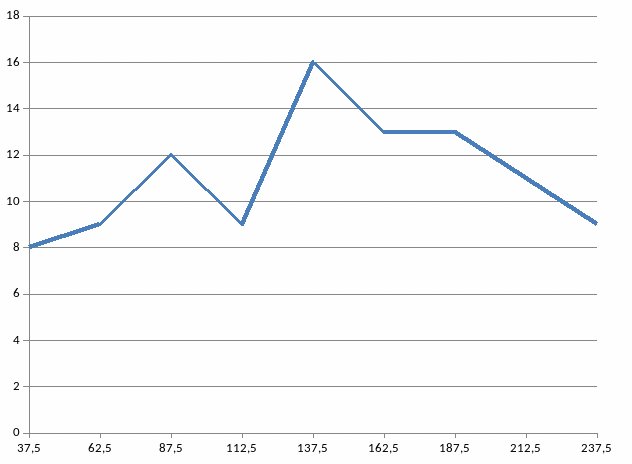
Строим гистограмму относительных частот:
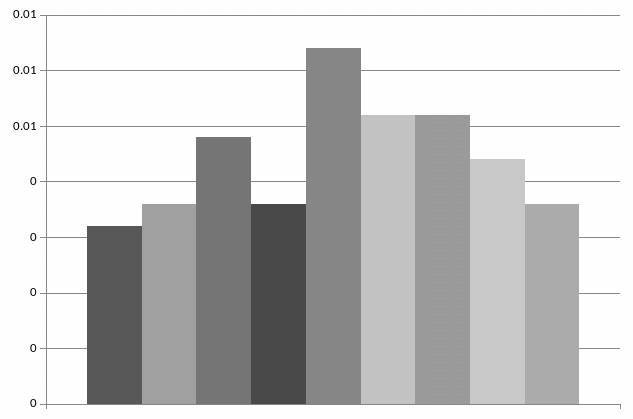
Строим эмпирическую функцию распределения:
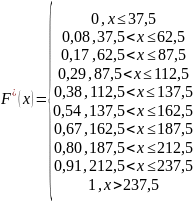
Строим график:
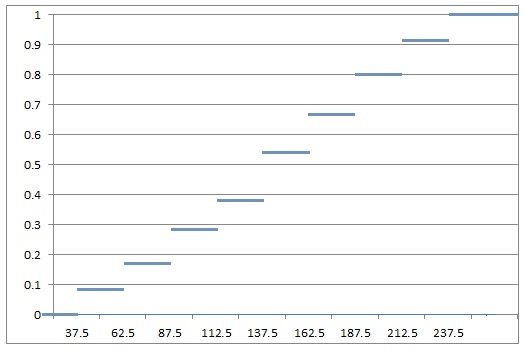
г) найдем числовые характеристики выборки:
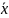 =
=
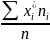 =
=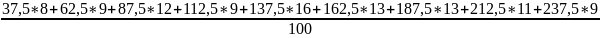 =
=
 = 141,5
= 141,5
=
 -
-
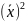 =
=
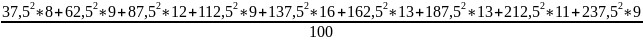 -
-
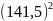 =
=
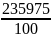 -
= 2359,75 – 20022,25 = 3571,5
-
= 2359,75 – 20022,25 = 3571,5
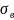 =
= 59,762
=
= 59,762
д) по критерию Пуассона необходимо сравнить эмпирические и теоретические частоты.
Найдем
теоретические частоты, для этого перейдем
к случайной величине
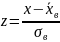 .
.
Вычислим
концы интервалов:
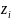 =
=
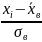 ;
;
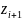 =
=
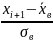 ,
,
получаем,
что
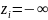 ,
,
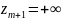 .
.
Если
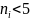 ,
то интервалы объединяем.
,
то интервалы объединяем.
Составим таблицу 3:
i |
|
|
|
|
|
|
|
1 |
25 |
50 |
8 |
- |
-91,5 |
- |
-1,531 |
2 |
50 |
75 |
9 |
-91,5 |
-66,5 |
-1,531 |
-1,113 |
3 |
75 |
100 |
12 |
-66,5 |
-41,5 |
-1,113 |
-0,694 |
4 |
100 |
125 |
9 |
-41,5 |
-16,5 |
-0,694 |
-0,276 |
5 |
125 |
150 |
16 |
-16,5 |
8,5 |
-0,276 |
0,142 |
6 |
150 |
175 |
13 |
8,5 |
33,5 |
0,142 |
0,561 |
7 |
175 |
200 |
13 |
33,5 |
58,5 |
0,561 |
0,979 |
8 |
200 |
225 |
11 |
58,5 |
83,5 |
0,979 |
1,397 |
9 |
225 |
250 |
9 |
83,5 |
- |
1,397 |
- |
Далее составляем расчетную таблицу 4, где находим теоретические частоты:
i |
|
|
Ф( ) |
Ф( ) |
|
|
1 |
- |
-1,531 |
-0,5 |
-0,4370 |
0,063 |
6,3 |
2 |
-1,531 |
-1,113 |
-0,4370 |
-0,3665 |
0,0705 |
7,05 |
3 |
-1,113 |
-0,694 |
-0,3665 |
-0,2549 |
0,1116 |
11,16 |
4 |
-0,694 |
-0,276 |
-0,2549 |
-0,1103 |
0,1446 |
14,46 |
5 |
-0,276 |
0,142 |
-0,1103 |
0,0557 |
0,166 |
16,6 |
6 |
0,142 |
0,561 |
0,0557 |
0,2123 |
0,1566 |
15,66 |
7 |
0,561 |
0,979 |
0,2123 |
0,3365 |
0,1242 |
12,42 |
8 |
0,979 |
1,397 |
0,3365 |
0,4192 |
0,0827 |
8,27 |
9 |
1,397 |
- |
0,4192 |
0,5 |
0,0808 |
8,08 |
Составляем таблицу 5:
i |
|
|
|
|
|
|
|
1 |
8 |
6,3 |
1,7 |
2,89 |
0,4587 |
64 |
10,1587 |
2 |
9 |
7,05 |
1,95 |
3,8025 |
0,5394 |
81 |
11,4894 |
3 |
12 |
11,16 |
0,84 |
0,7056 |
0,0632 |
144 |
12,9032 |
4 |
9 |
14,46 |
-5,46 |
29,8116 |
2,0617 |
81 |
5,6017 |
5 |
16 |
16,6 |
-0,6 |
0,36 |
0,0217 |
256 |
15,4217 |
6 |
13 |
15,66 |
-2,66 |
7,0756 |
0,4518 |
169 |
10,7918 |
7 |
13 |
12,42 |
0,58 |
0,3364 |
0,0271 |
169 |
13,6071 |
8 |
11 |
8,27 |
2,73 |
7,4529 |
0,9012 |
121 |
14,6312 |
9 |
9 |
8,08 |
0,92 |
0,8464 |
0,1048 |
81 |
10,0248 |
 = 4,6296
= 4,6296
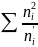 = 104,6296
= 104,6296
По
таблице критических точек распределения
 находим
находим
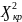 :
:
K
= 9 – 3 = 6 ,
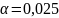
= 14,4.
Т.к.
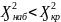 ,
то гипотеза о нормальном распределении
совокупности принимается.
,
то гипотеза о нормальном распределении
совокупности принимается.
е) Для оценки математического ожидания используем формулу:
-
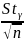
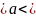 +
+
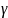 =
0,95 , t=1,96 ,
=
0,95 , t=1,96 ,
 =10
=10
= 141,5 , = 3571,5
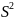 =
=
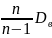 =
=
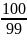 3571,5
= 3607,58
3571,5
= 3607,58
S = 60,063
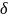 =
= 11,77
=
= 11,77
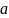
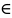 (141,5 –
11,77; 141,5 + 11,77)
(141,5 –
11,77; 141,5 + 11,77)
(129,73; 153,27)
S(1-q)
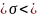 S(1+q)
S(1+q)
n = 100, = 0,95
q = 0,143
23,31 31,09

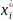
 =
=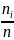
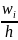
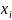
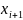
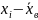
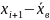
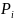 =Ф(
)-Ф(
)
=Ф(
)-Ф(
) =
n=100
=
n=100