
- •Основы физики неравновесных процессов
- •§1. Введение в кинетическую теорию. Математические методы описания неравновесных процессов.
- •§2. Одночастичные и многочастичные функции распределения. Иерархия уравнений Боголюбова для многочастичных функций распределения.
- •§3. Понятие о корреляционных функциях. Двучастичная корреляционная функция. Условие ослабления корреляции. Интеграл столкновений Больцмана. Кинетическое уравнение Больцмана.
- •§4. Некоторое применение кинетического уравнения Больцмана к равновесным системам. Распределения Максвелла и Максвелла-Больцмана.
- •§5. Кинетическое уравнение Больцмана в приближении времени релаксации.
- •§6. Понятие о турбулентности. Число Рейнольдса. Самоорганизация нелинейных диссипативных систем.
§4. Некоторое применение кинетического уравнения Больцмана к равновесным системам. Распределения Максвелла и Максвелла-Больцмана.
Рассмотрим самую простейшую ситуацию, когда система частиц находится в равновесии, а среда является однородной и внешние силы отсутствуют. В этом случае функция распределения является функцией только импульса
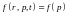 ,
,
тогда
 .
.
Непосредственно из интеграла столкновения следует:
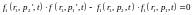
и
более коротко, поскольку от t
и
 ничего не зависит
ничего не зависит
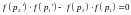 .
.
Прологарифмировав, получим
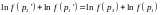 .
.
Поскольку
импульсы
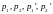 связаны законами сохранения импульса
и энергии
связаны законами сохранения импульса
и энергии
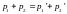 ,
,
 ,
,
то
общее решение для
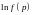 можно представить в виде линейной
комбинации функций: 1,
можно представить в виде линейной
комбинации функций: 1,
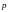 ,
p2.
,
p2.
В результате имеем:
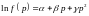 ,
,
где
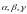 – пять постоянных, которые запишем
– пять постоянных, которые запишем
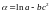 ,
,
 ,
,
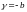 .
.
В
этом случае выражение для
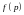 имеет вид
имеет вид
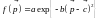 .
.
Пять
постоянных величин a,
b, и
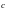 определяются из следующих пяти условий:
определяются из следующих пяти условий:
– условие нормировки
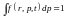 ,
,
– определение средней скорости
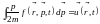 ,
,
– определение средней энергии
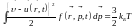 .
.
В итоге функция распределения имеет вид
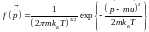 – распределение Максвелла
по импульсам.
– распределение Максвелла
по импульсам.
В
одномерном случае, поскольку
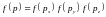
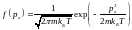 – одномерное распределение
Максвелла.
– одномерное распределение
Максвелла.
График функции одномерного распределения Максвелла имеет вид:

Поскольку распределение Максвелла обладает в импульсном пространстве сферической симметрий, то есть зависит только от абсолютной величины вектора (зависимость от квадрата импульса), то представляет интерес записать его в сферической системе координат:
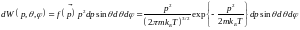 .
.
Интегрируя по θ и φ, получим плотность вероятности нахождения импульса в интервале от p до p + dp, независимо от направления
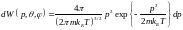
или
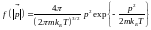 ,
,
распределение Максвелла по модулю импульса.
График функции распределения Максвелла по модулю импульса имеет вид:
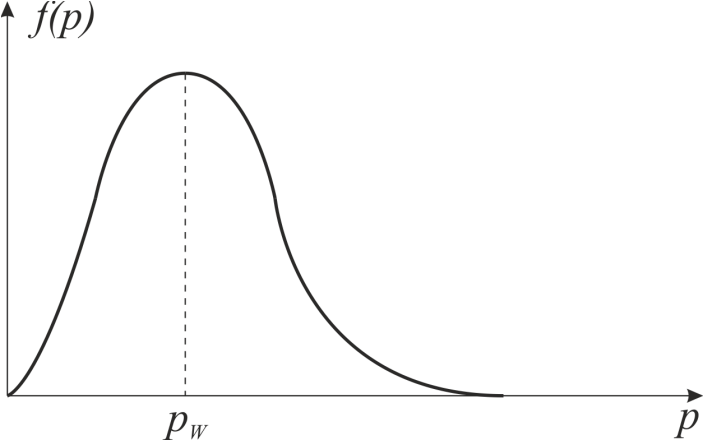
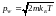 – наиболее вероятное значение
импульса;
– наиболее вероятное значение
импульса;
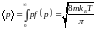 – среднее значение импульса;
– среднее значение импульса;
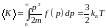 – среднее значение кинетической
энергии.
– среднее значение кинетической
энергии.
§5. Кинетическое уравнение Больцмана в приближении времени релаксации.
Обычно кинетическое уравнение Больцмана невозможно решить аналитически в достаточно общем виде, поскольку это неоднородное дифференциальное уравнение в частных производных. Рассмотрим поэтому сейчас наиболее простые ситуации с целью показать применение кинетического уравнения к анализу неравновесных процессов.
5.1. Рассмотрим процесс релаксации системы. Если произвольную систему с помощью внешнего воздействия вывести из состояния равновесия и затем внешнее воздействие выключить то спустя некоторое время система обязательно вернется в состояние равновесия, такой процесс называется релаксацией системы.
Запишем кинетическое уравнение Больцмана:
.
Рассмотрим систему из достаточно большого числа частиц, которая является однородной. Очень часто для моделирования различных процессов, и в частности процесса релаксации, используют модель интеграла столкновения в так называемом τ-приближении. В этом случае интеграл состояния можно записать в виде:
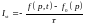 ,
,
здесь
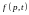 – функция распределения системы в
неравновесном состоянии,
– функция распределения системы в
неравновесном состоянии,
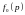 – функция распределения максвелла,
которая характеризует систему в состоянии
равновесия, а τ
– характерное время релаксации.
– функция распределения максвелла,
которая характеризует систему в состоянии
равновесия, а τ
– характерное время релаксации.
Поскольку
система была выведена из состояния
равновесия внешним воздействием, которая
затем была выключена и внешние силы
отсутствуют (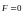 ),
с учетом этого кинетическое уравнение
Больцмана можно записать в виде:
),
с учетом этого кинетическое уравнение
Больцмана можно записать в виде:
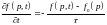 .
.
Это уравнение достаточно элементарно решается. Его можно переписать в виде:
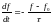 ;
;
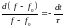 ;
;
интегрируя получаем
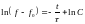 ;
;
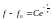 .
.
При t = 0 получим
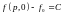 .
.
И тогда
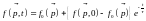 .
.
Если
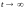 ,
то
,
то
 .
.
Из
решения видно, что в случае, когда время
превышает время релаксации
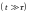 ,
функция распределения будет стремится
к максвеловскому распределению, т.е. к
состоянию равновесия.
,
функция распределения будет стремится
к максвеловскому распределению, т.е. к
состоянию равновесия.
5.2. Тау-приближение для расчета электропроводности в металлах.
Известно, что механизм электрического сопротивления определяется процессом рассеяния (столкновения) электронов на различных препятствиях внутри кристаллической решетки. Именно механизм электрического сопротивления определяет конечность величины электрического тока. Известно три основных механизма определяющих рассеяние электронов:
рассеяние электронов примесными атомами и не идеальностью кристаллической решетки (дислокацией), обычно вклад этого механизма в общий механизм сопротивления не велик;
электрон-элеткронное рассеяние или столкновение электрона с электроном, достаточно маловероятное событие;
электрон-ионное рассеяние или другими словами столкновение электрона с ионами кристаллической решетки, этот механизм является основным механизмом электрического сопротивления в металле.
Рассмотрим простейшую модель металла, которую представим в виде идеального кристаллической решетки с неподвижными, жестко закрепленными ионами. Внутри кристаллической решетки имеется газ электронов, которые могут свободно перемещаться в любом направлении решетки. Будем считать, что при отсутствии внешнего воздействия электронный газ внутри решетки покоится, таким образом, тепловым движением электронов мы так же пренебрегаем. Кроме того считаем, что электронный газ распределен по решетке однородным образом, а сам процесс электропроводности является стационарным во времени. Соответственно в рамках стационарного подхода в качестве внешнего воздействия выберем постоянное электрическое поле. Будем исходить из кинетического уравнения Больцмана, в котором интеграл состояния записывается в тау-приближении:
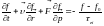 ,
,
τei – характерное время электрон-ионных столкновений.
Поскольку в качестве внешнего воздействия выбрано постоянное электрическое поле:
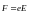 ,
,
кроме того, в силу стационарности задачи и однородно распределения электронов внутри решетки, производные по времени и по равны нулю. В итоге имеем
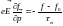 .
.
Представим исходную функцию распределения в виде:
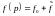 .
.
Тогда получим:
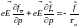 ,
,
Будем в дальнейшем искать только линейное приближение и вторым слагаемым в левой части последнего уравнения пренебрегаем.
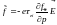 ;
;
Плотность тока равна:
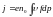 ;
;
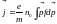 ;
;
 ;
;
первый интеграл равен нулю.
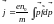 ;
;
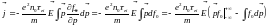 ;
;
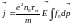 ;
;
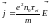 .
.
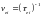 ;
;
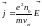 →
→ 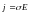 ,
,
где
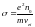 .
.
В рамках рассмотренной простейшей модели, электропроводность σ для конкретного металла практически является константой. Более сложные модели кристаллической решетки позволяют учесть зависимость электропроводности, а следовательно электрического сопротивления от температуры и частоты электромагнитного поля.
