§2. Одночастичные и многочастичные функции распределения. Иерархия уравнений Боголюбова для многочастичных функций распределения.

Как следует из предыдущего параграфа, вероятностный подход изучения систем, состоящих из огромного числа частиц, позволяет вычислить среднее значение величин как среднее по ансамблю. Однако как нетрудно видеть, микроскопическая фазовая плотность содержит огромное число исходных переменных. Для реального описания динамики системы представляется целесообразными значительно уменьшить количество информации о микросостоянии системы. Делается это следующим образом: количество переменных функции ρ можно уменьшить проинтегрировав по какой-то части из них.

Под одночастичной функцией распределения понимается следующая функция:

.

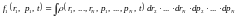Соответственно, двучастичная функция распределения будет определяться выражением:

.

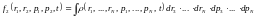И N-частичная функция распределения:

.

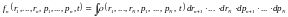Если f₁ проинтегрировать по координате

,

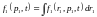то получим обычное уравнение Максвелла.

Если по импульсу

,

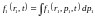распределение Больцмана.

Для того чтобы из одночастичной или двучастичной функции распределения можно было извлечь какую-нибудь информацию, для них нужно получить соответствующее уравнение. Их мы получим из исходного уравнения Лиувилля

,

.

Заменим переменные , .

,

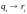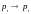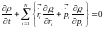Запишем функцию Гамильтона в следующем виде:

.

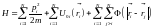Взаимодействие частиц между собой называется центральным, если их энергия взаимодействия является функцией модуля разности координат.

.

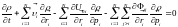Получим из этого уравнения уравнение для одночастичной функции распределения, проинтегрировав его по координатам и импульсам всех частиц кроме первой.

1. ;

2. ;

   1. ;

   2. ;

3. ;

1. ;

;

2. ;

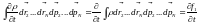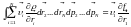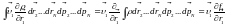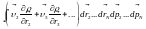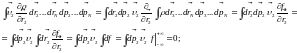
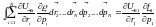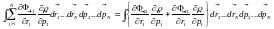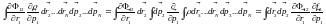
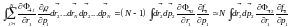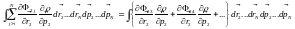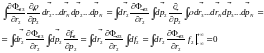
Подставим полученные результаты:

.

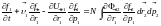Заменим,

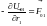– внешняя сила;

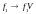– плотность на объем.

Уравнение для одночастиной функции распределения:

.

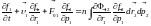Нетрудно видеть, что в правую часть уравнения для одночастичной функции распределения вошла двучастичная функция. Соответственно, если из исходного уравнения Лиувилля получить уравнение для двучастичной функции распределения, то в его правую часть войдет трехчастичная функция, в правую часть для трехчастичной функции распределения войдет четырехчастичная функция и т.д.

Таким образом, мы будем иметь бесконечную систему уравнений для одно-, двух-, трех-, многочастичных функций распределения. Такая система называется цепочкой или иерархией уравнений Боголюбова, и она полностью эквивалентна исходному уравнению Лиувилля.

Для того чтобы получить уравнение содержащее различной число переменных, необходимо сделать определенное предположение, упрощающее рассматриваемую модель.

§3. Понятие о корреляционных функциях. Двучастичная корреляционная функция. Условие ослабления корреляции. Интеграл столкновений Больцмана. Кинетическое уравнение Больцмана.

.

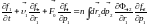Представим двучастичную функцию распределения в виде:

,

где g₂ – двучастичная корреляционная функция.

Отметим, что взаимодействие частиц друг с другом можно условно разделить на два этапа:

1. дальнее взаимодействие, которое происходит под действием электромагнитных полей;

2. ближнее взаимодействие, которое происходит хаотически, в виде столкновения или удара.

Записанное выше представление для функции f₂ как раз и разделяет взаимодействия на два этапа. При этом хаотический процесс столкновения и описывается корреляционной функцией. В данном случае речь идет о столкновении двух частиц, поэтому введена двучастичная корреляционная функция.

Рассмотрим ситуацию, когда имеет место одновременное столкновение трех и более частиц

.

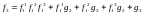Для того, чтобы разорвать бесконечную цепочку Боголюбова была выдвинута идея об ослаблении корреляции. Эта идея заключается в том, что одновременное столкновение все возрастающего числа частиц будет являться наименее вероятностным событием. Другими словами одновременное столкновение трех частиц будет происходить значительно реже, чем одновременное столкновение двух частиц. Соответственно, одновременное столкновение четырех частиц будет происходить еще значительно реже, чем одновременное столкновение трех частиц и т.д.

В самом простейшем случае будем считать, что вероятность столкновения трех частиц равна нулю, то есть корреляционная функция g₃ = 0. Это означает разрыв цепочки уравнений Боголюбова и фактически сведение описания системы у одному кинетическому уравнению.

В результате будем иметь:

.

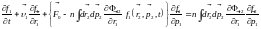Выражение в фигурной скобке в левой части представляет собой силу, воздействующую на частицу системы со стороны внешних полей и силу взаимодействия частиц друг с другом. Другими словами эта сила учитывает собственные поля, возникающие при движении частиц системы. Такие поля в физической кинетике называются самосогласованными, часто эти силы объединяют в одну и обозначают 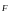– сила воздействия на частицу системы с учетом самосогласованного поля.

Выражение в правой части описывает парные столкновения частиц друг с другом, и для его вычисления необходимо выбрать конкретную модель столкновения двух частиц.

Впервые такую модель предложил Больцман. Он же вычислил правую часть, которая получила название интеграла столкновений.

Больцман предложил считать сталкивающиеся частицы системы абсолютно упругими шариками радиуса R, и в результате он получил интеграл столкновения в виде:

,

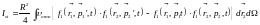где υ_отн – относительная скорость сталкивающихся шаров;

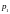и – и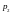мпульсы шаров до столкновения;

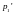и – и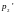мпульсы шаров после столкновения;

Ω – элемент телесного угла в пространстве импульсов.

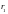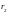Нетрудно видеть, что интеграл столкновения является функцией , , t, поскольку по и фактически производится интегрирование, а импульсы и выражаются через и с помощью законов сохранения импульса и энергии. В этой связи, опуская индекс 1, запишем:

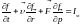– кинетическое уравнение Больцмана.

Отмеченное выше условие ослабления корреляции имеет свои границы применимости. Это условие справедливо если концентрация частиц в единице объема достаточно мала, то есть фактически речь идет о газовом приближении. Действительно, кинетическое уравнение Больцмана справедливо практически для любых газов. Как не парадоксально, но кинетическое уравнение применяют для исследования процессов диффузии, теплопроводности и в твердых телах.

В данном случае речь идет об электронном газе внутри кристаллической решетки. (К жидкостям кинетическое уравнение Больцмана не применимо).