Методика реалізації моделі

Перша таблиця містить дані про вартість перевезень тонни сировини від постачальників до пунктів переробки (рядки – постачальники, стовпці – пункти переробки). У крайньому правому стовпці вказуємо запаси сировини кожного постачальника.

Друга таблиця включає дані про кількість сировини, яка перевезена від постачальників до пунктів переробки. На початку ці значення приймаємо рівними 0.

Останній рядок і останній стовпчик – це загальні кількості перевезень від кожного постачальника до кожного пункту переробки (суми за стовпцями та рядками).

У третій таблиці вказуємо вартість перевезень від постачальників до пунктів переробки, які визначаються шляхом множення елементів першої таблиці на відповідні елементи другої.

Визначаємо загальну вартість для постачальників, пунктів переробки і для всієї таблиці.

Четверта, п'ята і шоста таблиці аналогічні першій, другій та третій, але вони визначають перевезення напівфабрикатів від пунктів переробки до споживачів (рядки – споживачі, стовпці – пункти переробки).

Останній стовпець четвертої таблиці – потреби споживачів.

Сьома таблиця включає дані про переробку сировини; кількість стовпців відповідає кількості пунктів переробки.

1-й рядок – вартість переробки тонни сировини.

2-й рядок – кількість переробленої сировини.

3-й рядок – вартість переробки.

2-й рядок повинен дорівнювати кількості доставленої сировини (останній рядок другої таблиці).

Визначаємо загальну кількість і вартість переробленої сировини.

Цільовою клітинкою є сума загальної вартості перевезень і переробки сировини.

Змінними є клітинки другої та п'ятої таблиць.

Обмеження:

1. кількість вивезеної сировини від постачальника дорівнює запасам;

2. кількість напівфабрикатів, доставлених споживачам дорівнює потребам споживачів;

3. уся сировина, що доставлена на пункт переробки, переробляється на напівфабрикати та вивозиться;

4. кількість перевезень – невід'ємне число.

Лабораторна робота №7 Тема: „Розподіл коштів між виробництвами” Постановка задачі

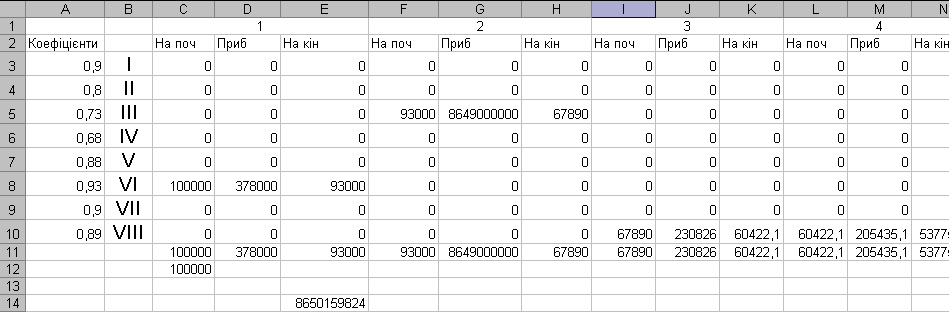
Є певна сума коштів, які можна вкласти в різні види виробництва. Виробництво, яке отримає кошти, дає річний прибуток, який є відомою функцією від кількості вкладених коштів. У результаті процесу виробництва кількість вкладених коштів зменшується на певний відсоток. На початок наступного року кошти, які залишились, перерозподіляються. Визначити такі розподіли, при яких прибуток за всі роки буде максимальний.

Економіко-математична модель задачі

Параметри:

п – кількість виробництв, які об’єднані єдиним керівництвом.

W – передбачені кошти для розвитку виробництв.

W₁ⁱ, W₂ⁱ, W₃ⁱ,…, W_пⁱ – кошти, які були виділені виробництвам на початок i-того року.

G_j(W_j) – прибуток, який дає виробництво, що залежить від кількості вкладених в нього коштів.

Β_j – коефіцієнт пропорційності, , який показує зменшення кількості коштів у результаті виробничої діяльності.

Обмеження:

Для початкового розподілу W₁⁰+W₂⁰+W₃⁰+…+W_п⁰=W.

При перерозподілі W₁ⁱ⁺¹+W₂ⁱ⁺¹+W₃ⁱ⁺¹+…+W_пⁱ⁺¹= β₁W₁ⁱ+ β₂W₂ⁱ+ β₃W₃ⁱ+…+ β_пW_пⁱ.

Критерій:

g₁(W₁⁰)+ g₂(W₂⁰)+ g₃(W₃⁰)+…+ g_n(W_n⁰)+ g₁(W₁¹)+ g₂(W₂¹)+ g₃(W₃¹)+…+ g_n(W_n¹)+ g₁(W₁²)+ g₂(W₂²)+ g₃(W₃²)+…+ g_n(W_n²)+…+ g_n(W₁^n-1)+ g₂(W₂^n-1)+ g₃(W₃^n-1)+…+ g_n(W_n^n-1) → max