43. Лінійні функціонали. Означення, прик., неперервність, обмеженість , норма.

Озн: Нехай Е – лінійний простір, відображення f лінійного простору Е в числову вісь назив. функціоналом (f: E→R). Озн. Функціоналом назив. адитивним, якщо Озн. Функціоналом низив. однорідним і виконується . Озн. Функціонал назив. лінійним, якщо він адитивний та однорідний, тобто виконується так умова . .

Озн. Функціоналом назив. додатно однорідним, якщо .

Озн. Функціонал назив. опуклим, якщо викон. така умова

. Озн. Функціонал назив. однорідно опуклим, якщо він додатно однорідний і опуклий. Нехай є лінійний топологічний простір (ЛТП). Частинним випадком лінійного топологічного простору є метричні простори. Для функціоналів, заданих на ЛТП природнім є питання вивчення неперервності цих функціоналів. Озн. Лінійний функціонал назив. неперервним х, якщо - окіл т.х такий, що . Озн. Функціонал назив. неперервним на Е, якщо він неперервний в кожній точці цього простору. Якщо на ЛТП викон. І-ша аксіома зліченості,зокрема до таких просторів належать метричні простори, то озн. неперервності можна дати так:

Озн. функціонал низив. неперервним, якщо Структура лінійності на лінійному топол. Просторі дозволяє пересувати околи, тобто якщо U(0)-окіл, то наступна множина є околом т.х. Ця властивість дозволила перевіряти неперервн. формулу в одній єдиній. Функціонал називається неперервним, якщо він неперервний в т. 0.

Теорема: Функціонал, заданий на лінійному топологічному просторі є непер. Тоді і тільки тоді коли він обм. в деякому околі т.О.

Доведення:

Функціонал непер. функціонал непер. в т.О . Остання нерівність озн. обмеженість в т.О.

=f-обмежений в U(0). Нехай функціонал обм. в U(0), тобто

такий, що . Доведено. ця теорема встановлює зв'язок між непер. і обмеженістю. Розглянемо лінійні функціонали на нормованому просторі.

Нехай Е-норм. Простір f – лінійно неперервна функційована на F. З попередньої теореми випливає, що цей функціонал є обмежений в деякому околі т.О, але в нормованому просторі в будь-який окіл т.О можна поміститися відкритою кулею, тобто функціонал буде обмеженим на цій кулі. Не обмежуючи загальності будемо вважати, що ми маємо одиничну кулю, тобто лінійно неперервний функціонал на нормованому просторі є обмеження на одиничній кулі. В зв’язку з цим природним є наступне означення.

Озн. Нормою функціонала f називається точна верхня грань абсолютних значень функціонала на одиничній кулі: . Означення норми функціонала можна дати іншим еквівалентним способом:

Озн.Нормою функціонала ниаивається 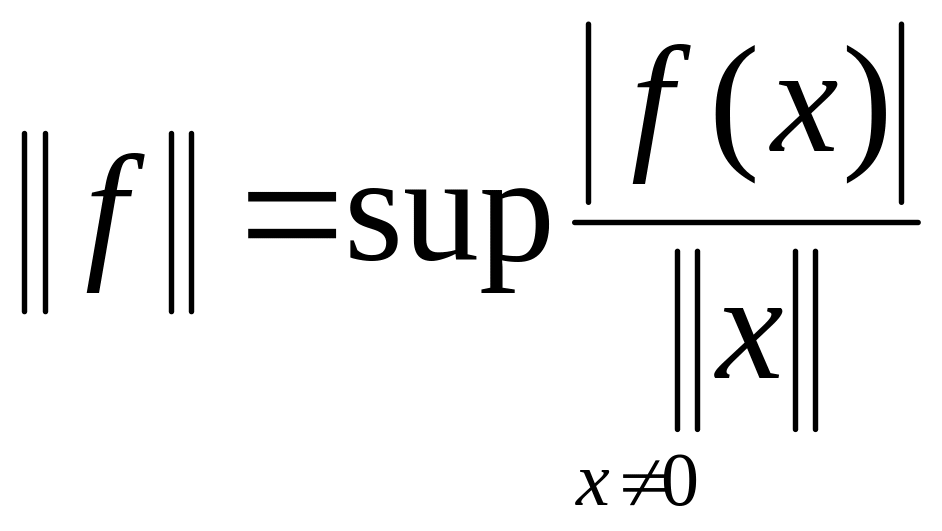. Покажемо їх еквівалентність. Візьмемо . Роглянемо . Очевидно, що . Тобто у належній одиничній кулі. Таким чином . Якщо взяти sup в цій рівності, то отримаємо .

Приклади лінійних функціоналів на нормованих просторах

1. 

- фіксований вектор.

Лінійність очевидна.

Неперервність. В скінченно вимірних просторої всі лінійні функціонали автоматично неперервні, а отже і обмежені. Тому існує норма, яку знайдемо Використаємо нерівність Коші-Баняковського

При . З (2), (3) випливає, що

2. простір неперервних на [a,b] функцій і для визначимо функціонал 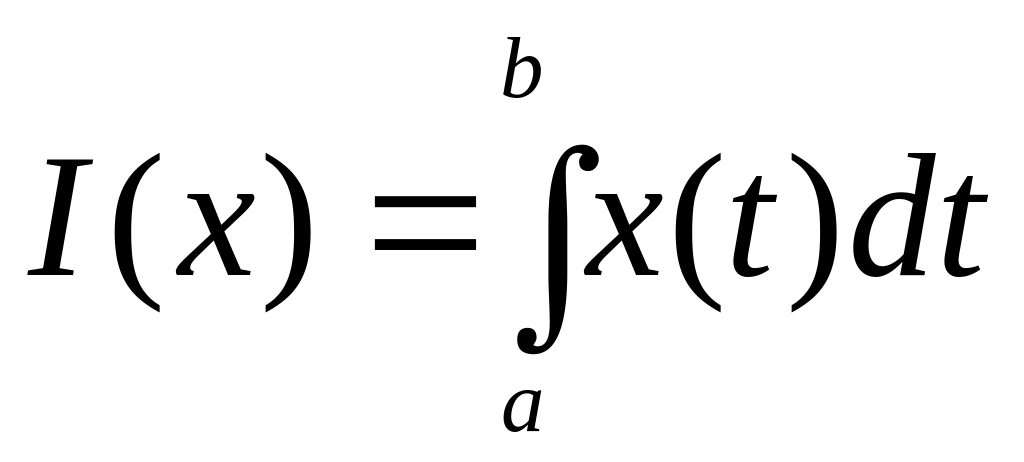. Відомо, що цей функціонал є лінійним та неперервним.

Знайдемо норму цього функціонала. Для цього знайдемо 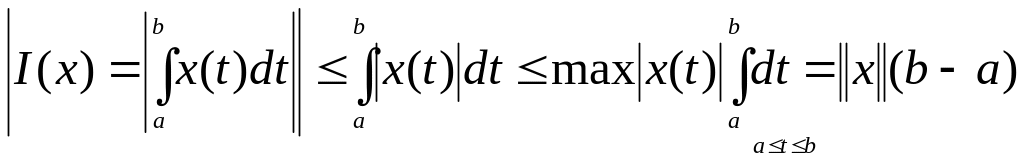. Звідси . Якщо замість x(t), взяти const в нерівності (4) дёосягається рівність. А отже

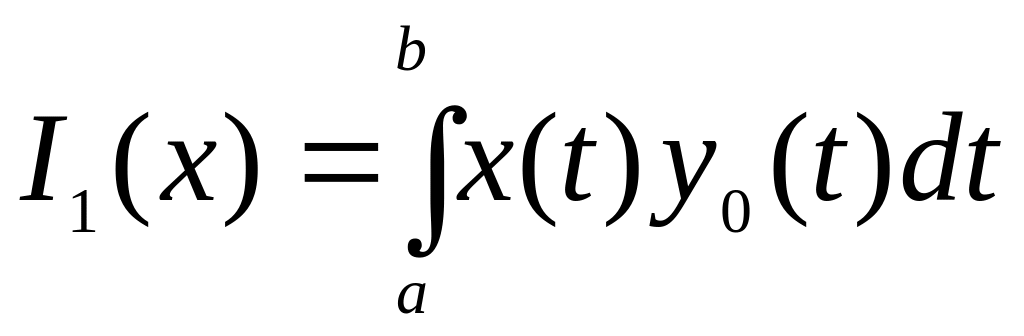3. , де - фіксована функція. Цей функціонал теж є лінійний і неперервний і 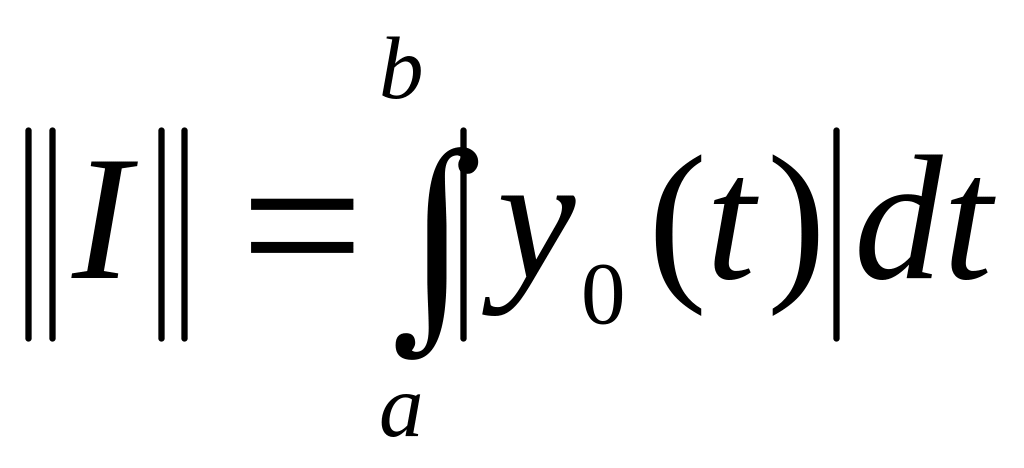. Нехай Е-довільний евклідовий простір і а є Е – фіксований елемент. Визначимо функціонал

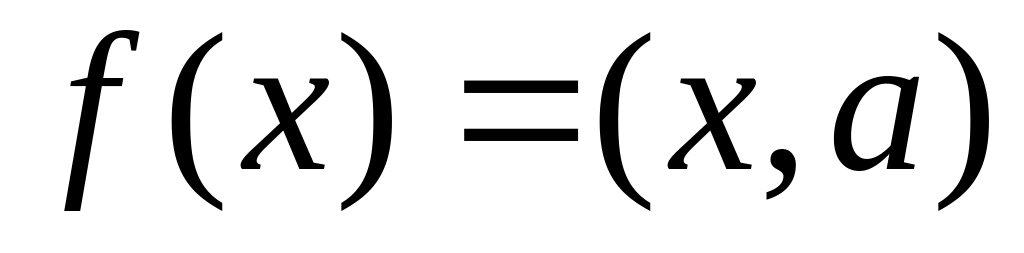
4. Дельта функція Дірака. Нехай . Припустимо о є [a,b] 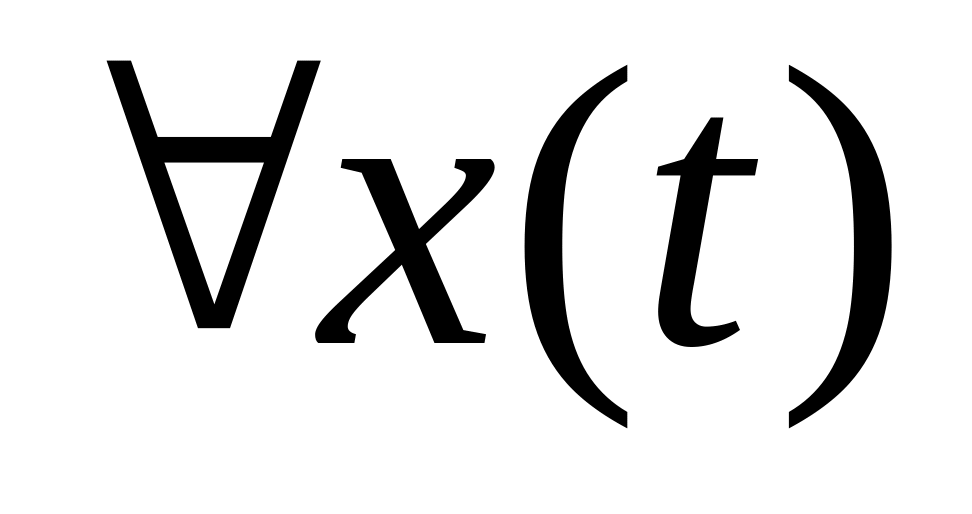визначимо 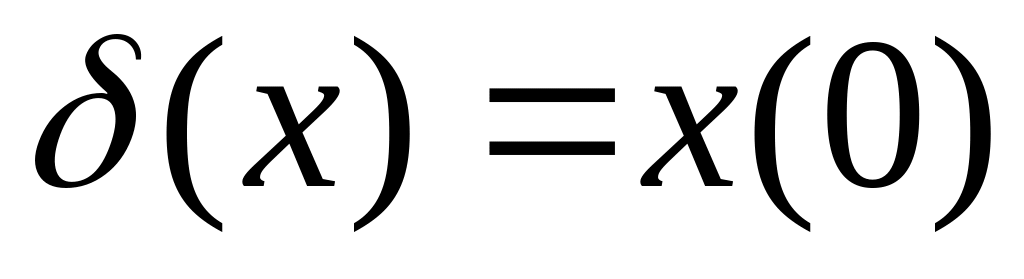. Цей функціонал є лінійний та неперервний 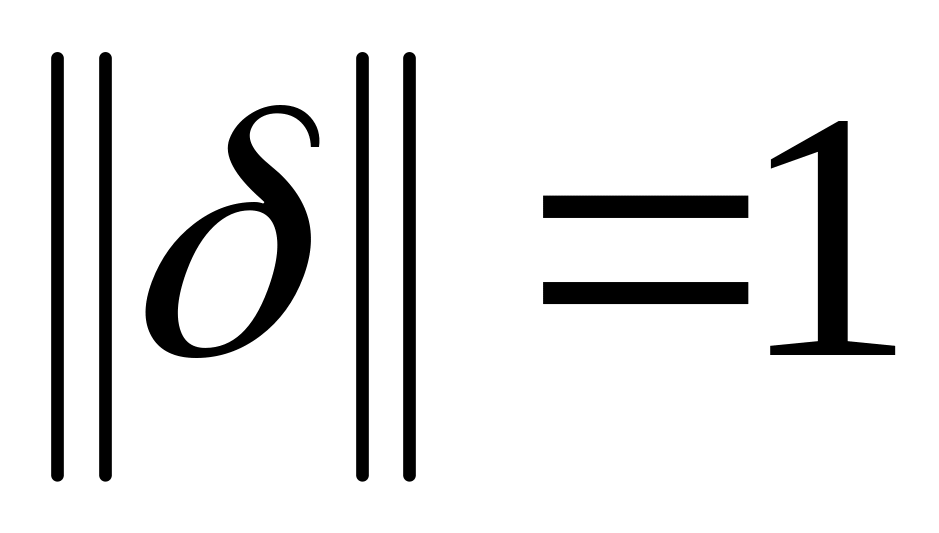. Спряжений простір

Нехай Е – лінійний топологічний простір на множині та неперервності функціоналів, що діють в просторі Е введемо дві операції

1. Додавання. 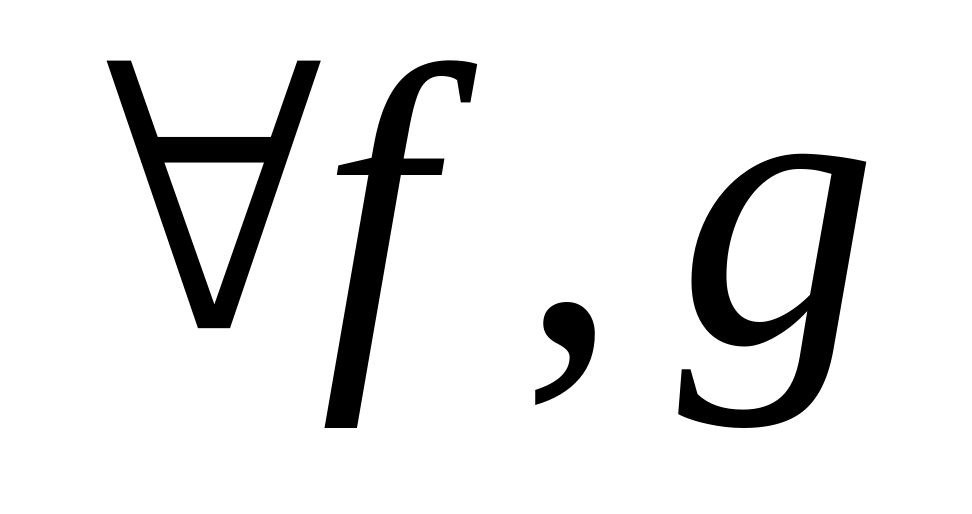- лінійних неперервних функціоналів над Е введемо операцію додавання так: Назвемо сумою f+g такий функціонал, який кожному

2. Множення на число. Добутком лінійного неперервного функціонала над Е на назвемо такий

Із введеними операціями множина лінійних неперервних функціоналів набуває структури лінійного простору. Вище ми ввели означення норми функціонала. Не важко показати, що це означення задовольняє всі аксіоми норми, тобто множина лінійних неперервних функціоналів є нормованим простором.

Означення. Спряженим простором до простору Е називається множина всіх лінійних неперервних функціоналів над Е. позначається .

Теорема: Спряжений простір до нормованого простору є банановим.

Доведення:

Нехай f₁,f₂,…,f_n – фундаментальна послідовність неперервних функціоналів. Нам потрібно показати, що ця послідовність є збіжною. Це означає

Враховуючи попередню нерівність маємо, що

. Остання нерівність означає, що в кожній точці t числова послідовність є фундаментальною, а отже і збіжною бо простір R є повним.

Нехай f(t) – початкова границя цієї послідовності . Покажемо, що він є лінійний, неперервний і є границею послідовності f₁,f₂,…,f_n в топології, що визначається нормою функціонала.

Лінійність є очевидною

Для доведення неперервності перейдемо до границі в такій нерівності:

при .

Оскільки ліва частина в m зам., а права – ні, то до границі можна перейти.

- обмежений.

Обмеженим буде і і також - неперервний.

Те, що функціонал f є границею послідовності в топології, що визначається нормою функціонала випливає з нерівності . Доведено.

Зауваження: Остання теорема стверджує, що спряжений до нормованого простору є повним не залежно від того чи є повним вихідний простір.

Теорема Гана-Банаха.

Нехай, Е – лінійний простір, p(x) – фіксований, однорідно опуклий функціонал, L – підпростір в Е. тоді кожен лінійний функціонал f, що заданий на L, який задовольняє умову може бути продовжений на весь простір Е із збереженням умови (*).

Теорема Гана-Банаха для нормованих просторів.

Нехай Е – нормований простір f(x) – фіксований функціонал, L – підпростір. Тоді кожен лінійний функціонал f₀, що заданий на L і задовольняє умову на L може бути продовжений на весь простір Е із збереженням норми.