42.Евклідові простори: означення, осн.Прик., зв'язок з нормованими просторами, нерівність Коші – Буняковського.

Озн. Нехай - лінійний простір. Кажуть, що на просторі задано скалярний добуток, якщо на ньому задана числова ф-ція двох аргументів, яка познач. , яка володіє такими властивостями

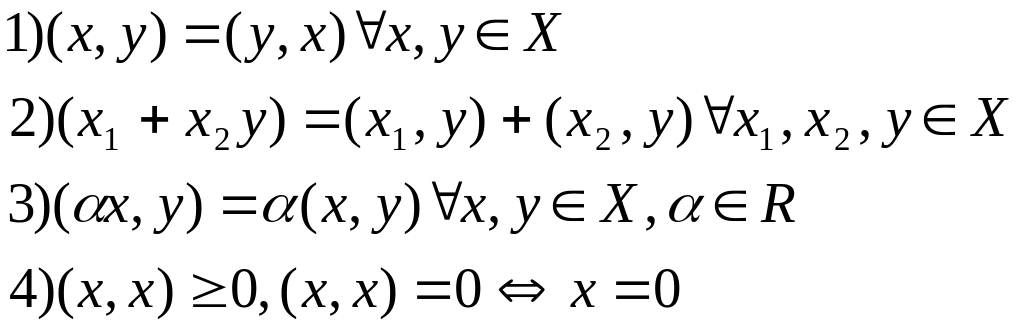
Озн. Евклідовим простором називається лінійний простір на якому вв скалярний добуток.

Кожен евклідовий простір є нормованим. Норма у кожному вв наступним чином .

Доведення того, що норма спирається на властивості скалярного добутку і на нерівність коші-Боняковського .

Поряд з тим, що в евклідовому просторі визначається поняття скалярного добутку можна ввести поняття кута між кутами, а саме кута між векторами х,у називається . З нерівності Коші-Боняковського випливає, що права частина останньої рівності завжди за абсолютною величиною не перевищує 1. тому поняття кута таким чином ввести можна.

Озн. Два вектори х і у називаються ортогональними, якщо їх кут .

Будь-яка система ненульових ортогональних векторів завжди є лінійно незалежна, тобто =0 і всі - попарно ортогональні.

Дійсно, помножимо останню рівність скалярно на

Озн. Система векторів називається ортонормованою, якщо ці вектори попарно ортогональні і норма кожного елемента =1

- ортонормовані

Кожна ортогональна система може бути зроблена ортонормованою, а саме, якщо - ортогональна, то - ортонормована система.

Озн. С-ма векторів називається повною, якщо найменший замкнутий лінійний простір, який містить цю систему співпадає з усім простором.

Озн. Ортогональним (ортонормованим) базисом називається повна ортогональна (ортонормована) с-ма.

Приклади евклідових просторів і ортонормованих базисів на них

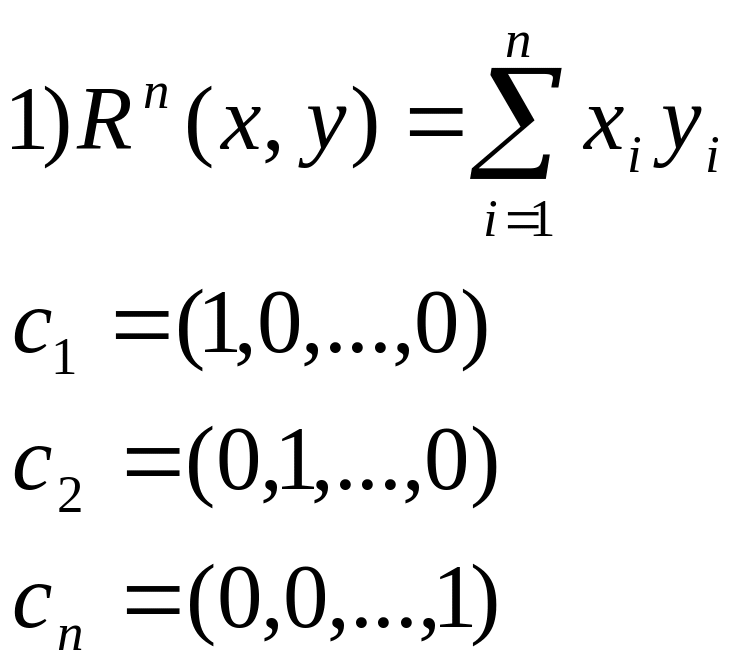
Зауважимо, що в цьому просторі є ще безліч ортонормованих базисів

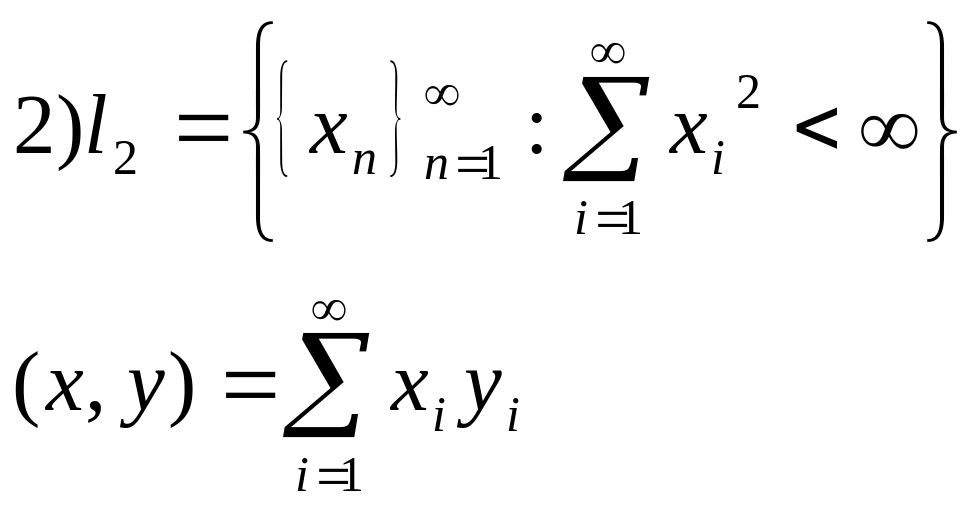
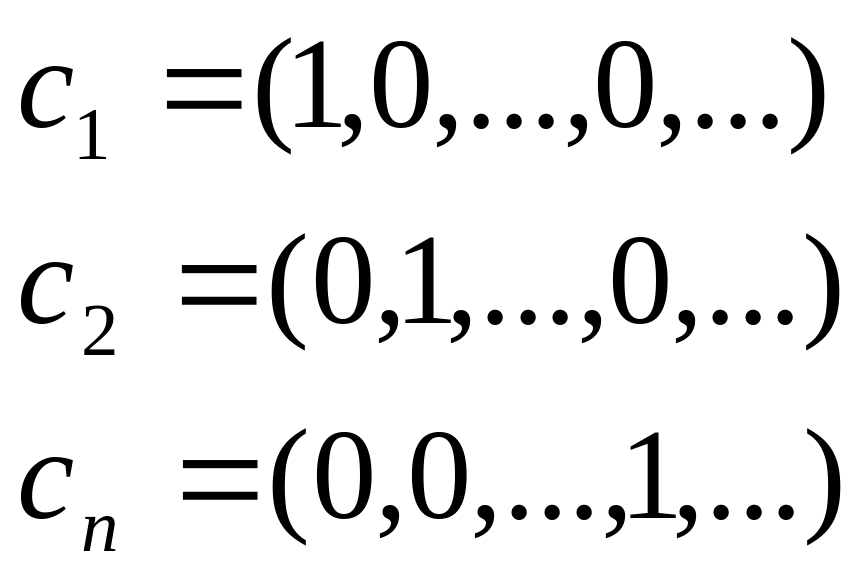
3)

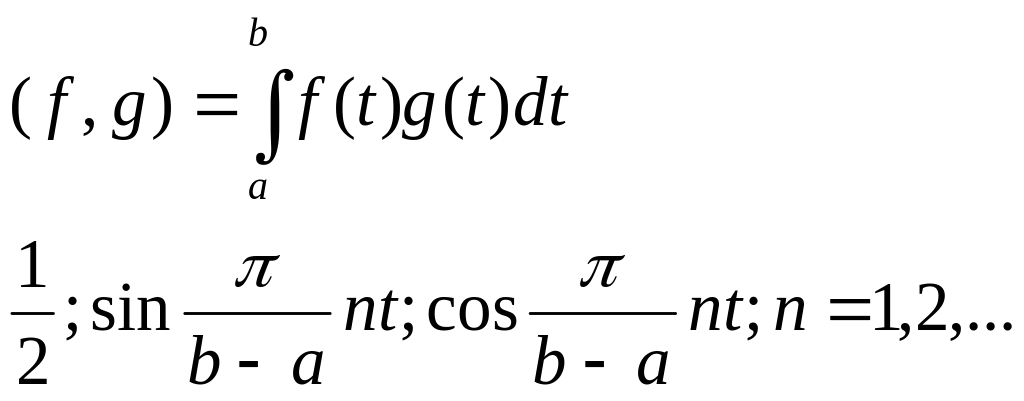
Зокрема, коли розглянути будь-який простір с то с-ма векторів набуде вигляду

Розглянемо сепарабельний евклідовий простір. Покажемо, що в такому просторі кожен ортогональний базис не може бути більшим ніж зліченний.

Нехай х- сепарабельний евклідовий простір. - ортонормований базис.

Побудуємо кулі виду , вони не перетинаються. Оскільки простір сепарабельний, то в ньому існує зліченна всюди щільна множина, тобто в кожній побудованій кулі знайдеться принаймні 1 точка з цієї множини, а оскільки множина зліченна то й к-ть куль не може бути більша, ніж зліченна, а отже ортонормований базис теж зліченний.

Вище наведені приклади є сепарабельними просторами, тому ортонормовані базиси в них зліченні.