40.Повні метричні простори. Повнота простору с[a,b].

Метричний простір в якому всяка фундаментальна послідовність є збіжною називається повним метричним простором.

Н. - фундаментальна послідовність у просторі С[a,b], це означає. Що кожна з функцій є неперервною на відрізку [a,b] і виконується нерівність . З останньої нерівності випливає, що , тобто послідовність задовольняє критерій К рівн. збіж., а отже є збіжною послідовністю. Границя рівн., збіжності послідовності неперервних ф-цій теж є неперервною ф-цією., яку ми позначали . Пере., при кожній фіксованій t до границі в попер. нерівності при , отримаємо, що , тобто , або що те саме , а це означає, що і повнота цього простору доведено.

Принцип стискаючих відображень.

Озн. Нехай маємо метричний простір R і A — відображення з R в R.(самого в себе)

Відображення А називається стискаючим або стиском, якщо . (1)

Теорема: (принцип стискаючих відображень): В повному метричному просторі кожне стискаюче відображення має нерухому точку, тобто таку точку, для якої виконується умова: , причому ця точка єдина.

Доведення: Перш за все, кожне стискаюче відображення є неперервним. Дійсно, нехай , тобто , тоді з нерівності (1) випливає: , а це означає, що . А це означає неперервність.

Нехай — довільна метрика простору R.

Побудуємо послідовність наступним чином:

(*)

Покажемо, що ця послідовність є фундаментальною.

Нехай для визначеності , тоді

Скористаємось нерівністю (1) і після n використань матимемо:

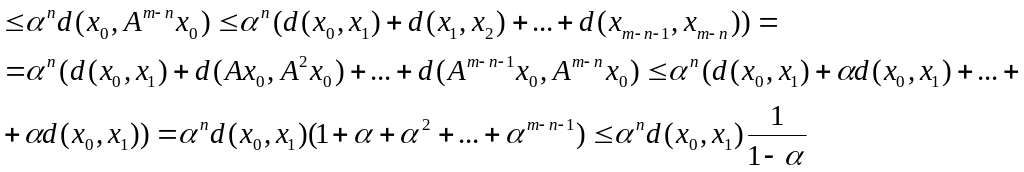Тобто ми довели таку нерівність:

Зрозуміло, що при зростанні n права частина може бути зроблена як завгодно малою, тобто послідовність фундаментальна. Оскільки метричний простір повний, то ця послідовність збіжна, тобто — збіжна .

Покажемо, що ця точка x є нерухомою точкою відображення А. Дійсно, . Отже, , тобто ми довели існування нерухомої точки.

Покажемо єдність нерухомої точки.

Припустимо, що ця точка не єдина, тобто (2)

Нерівність (1) має вигляд . Оскільки , то звідси випливає, що , а це є протиріччя.

Теорему доведено.

41. Нормовані простори: озн., основні прик., звязок з метричними просторами, повнота.

Задано лін простір Х і поставимо у відповідність кожному елементу , деяке число , так щоб виконувались наступні аксіоми:

1)

2)

3) .

Число називається нормою елемента х, а сам лін простір для якого для кожного елемента визначається норма називається нормованим простором. Всякий нормований простір легко перетворити у метричний, якщо покласти, що . Якщо в цій рівності покласти, що у=0, ми отримаємо, що . Якщо в метричному просторі можна ввести операції додавання і множення на число, і покласти ми отримаємо нормований простір.

Приклад.

Приклад.

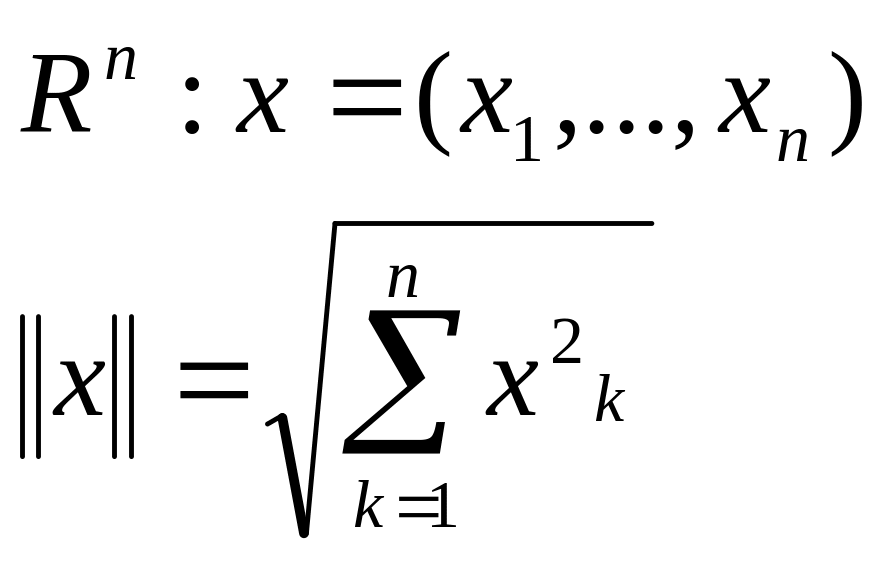
Приклад.

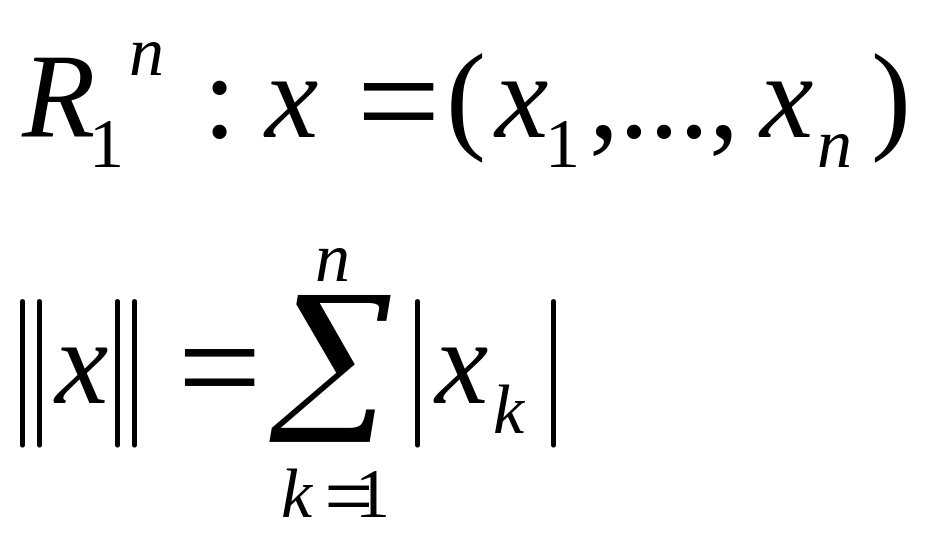
Для нормованих просторів так як і для метричних просторів можна вводити поняття збіжності послідовностей:

Т.ч. поняття границі у нормованому просторі еквівалентне поняттю границі введеному у метричному просторі. Аналогічними будуть поняття еквівалентних послідовностей.

Нормований простір в якому всяка фундаментальна послідовність є збіжною називається повним нормованим простором. Вони ще мають іншу назву Банахові простри.

Так само можна ввести поняття підпростору для нормованого простору.

Пр. У назв. Підпростором нормованого простору Х, якщо У<X і У є підпростором простору Х, як підпростір і норма введення в У така сама, як норма для елементів Х, але тут додають ще додаткову вимогу, щоб У був замкнутим. Якщо ця ум. Не виконується, то У називають не підпростором, але лише лін. многостатністю.