38 Частинні похідні. Похідна за напрямом. Градієнт. Рівність змішаних

частинних похідних.

Тоді . Застосуємо теорему Лагранжа : . Тепер ф-ю можна записати: . Тепер навпаки: . Перейдемо до границь при . В силу неперервності вийде: щ. т. д. ця теорема переноситься на випадок змінних і змішаних похідних вищих порядків.

Похідна за напрямом

Нехай маємо деякий заданий напрям і ф-я швидкість зміни ф-ї.

Означення: похідною від ф-ї f(M) в т. M₀ за напрямом l називають границю , де - норма (довжина вектору). Така границя позначається Ця функція характеризує «швидкість зміни» вказаної функції в точці M₀ за напрямком l.

Запишемо р-ння відрізка де довжина . Зокрема, якщо задано напрям, то задані напрямні косинуси . Тоді . ю А напрямні косинуси фіксовані, бо напрямок задано. Маємо тому .

Нас цікавить, коли максимальна, за яким напрямом швидкість ф-ї найбільша.

Означення: Вектор називається градієнтом величини f та його позначають g=gradf. З формули похідної по напрямку випливає, що градієнт є вектор якій за численним значенням та за напрямком характеризує найбільшу швидкість зміни величини f..

. Маємо

.

39. Диференційовність ф-ції багатьох змінних. Достатні умови

диференційовності.

Розглянемо -повний приріст, якщо розглядати приріст по одній змінній - частинні прирости. Для функції однієї змінної маємо (1)

(2)

Якщо виконується (1), то ми говоримо, що функція диференційовна в точці . Покажемо аналогічну рівність для функції багатьох змінних.

Означення диференційовності в точці для функції багатьох змінних. Говорять, що функція диференційовна в точці , якщо повний приріст функції в точці дорівнює (3), де , коли всі не залежно одне від другого.

Для функції однієї змінної щоб була формула (1), (2) необхідно і досить щоб існувала скінченна похідна в точці , тому функцію яка має в точці полхідну називається дмференційовною. Але для функції двох змінних (3) не виконується, якщо існують скінченні частинні похідні, тобто функція не є диференційовною в точці .

Розглянемо 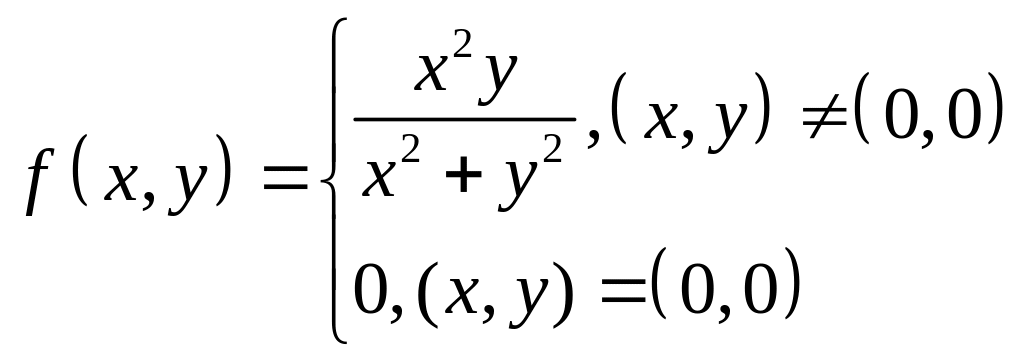Розглянемо повний приріст функції в 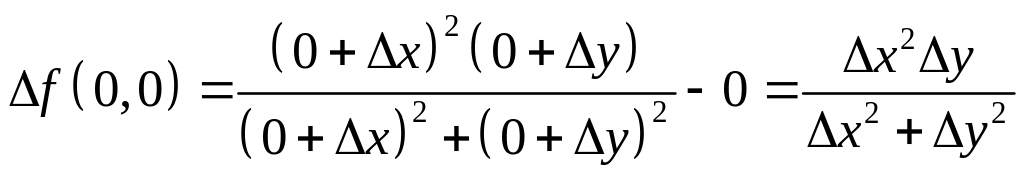. Знайдемо похідну по в точці

, , , ,

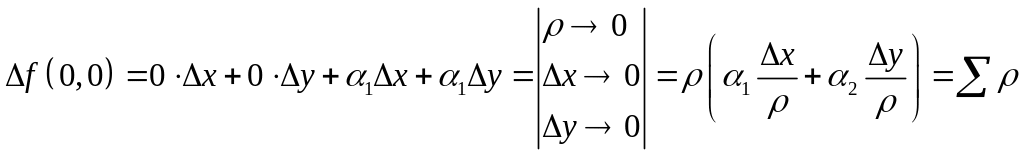
Ми маємо, що , коли

Переконаємося, що

Візьмемо

Отже з існування похідних не випливає (3) є достатні умови диференційовності.

Теорема. Якщо визначена в і в точці та деякому околі точки , що міститься в , , що має частинні похідні по всіх змінних і ці похідні неперервні в точці , то функція диференційовна в і її повний приріст в , де як тільки не залежним одним від другого.

39. Диференційовність ф-ції багатьох змінних. Достатні умови диференційовності

Доведення. Знайдемо повний приріст функції в точці . Додамо і віднімемо такі значення функції, щоб мати часткові прирости, по одній змінній

Кожен раз розглядаємо приріст, як приріст функції однієї змінної. До кожного приросту застосуємо теорему Лагранжа про скінченні прирости . Це можна зробити, якщо вибрати настільки малими, щоб вони попали в той окіл точки , про який йде мова в теоремі. Будемо мати:

(4)

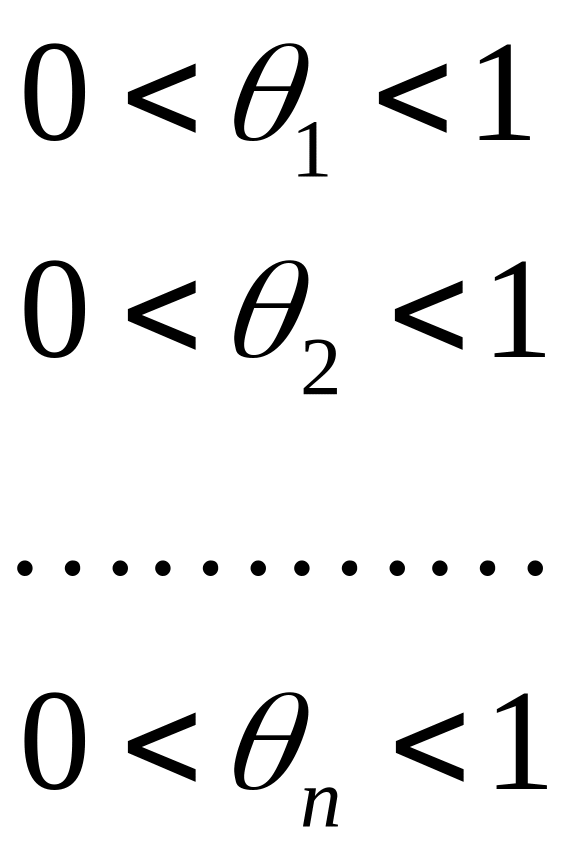. За теоремою Лагранжа.

Використаємо те, що похідні неперервні в . Неперервність означає: (5)

Використаємо властивості границь (6)

якщо

Підставимо (6) у (4)

.

(3) доведено.

Зауваження 1.Для компактності запису (3) запишемо ці нескінченно малі через відстань

де якщо

Отже (3) має вигляд: , то .

Зауваження 2. Означення диференційовності можна давати в такому вигляді: називається диференційовною в , якщо, сталі, такі що 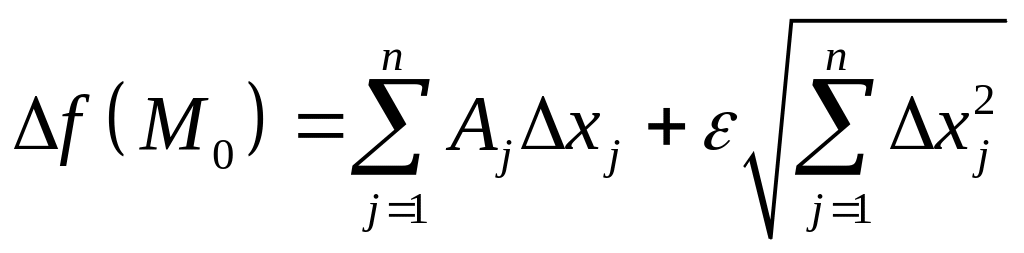(3’), де як тільки . З доведеної теореми вмдно, що .