35. Почленне інтегрування і диференціювання.

Теорема1. Якщо функції , неперервні на і ряд (1) збігається на проміжку цьому проміжку рівномірно, то інтеграл від суми ряду (1) представляється у вигляді (2).

Довед. Проінтегрувавши тотожність на проміжку , одержимо: 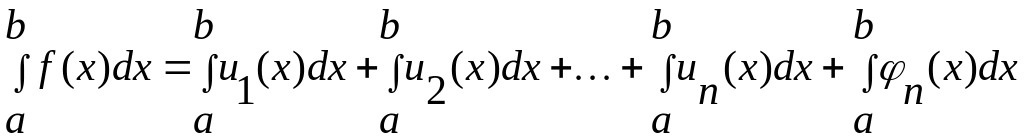. Таким чином сума членів ряду (2) відрізняється від інтеграла 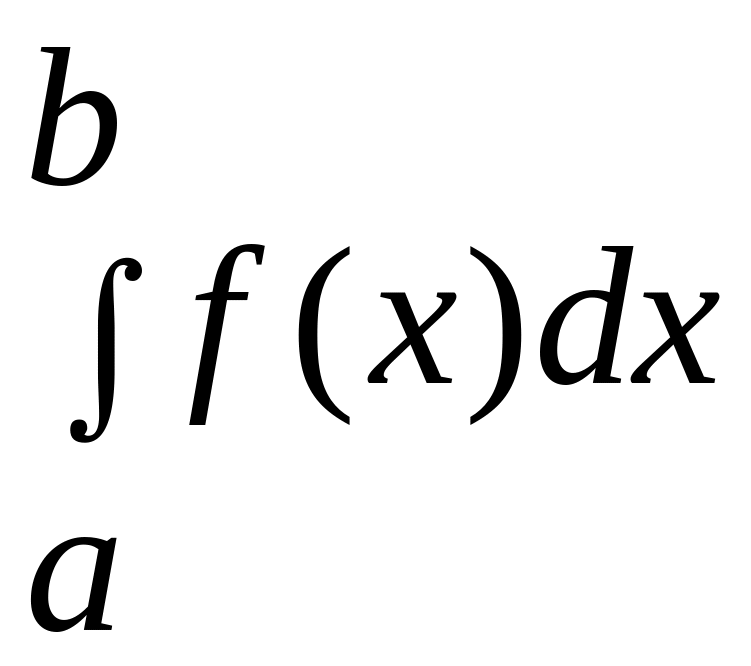додатковим членом 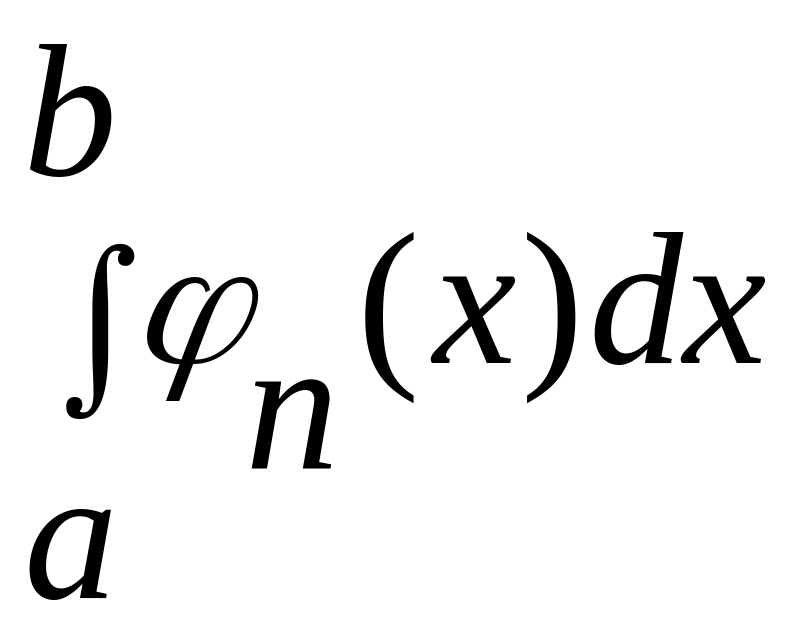. Для доведення (2) потрібно довести, що (3). В силу рівномірності ряду (1), для будь-якого знайдеться номер такий, що при для всіх . Тоді що і доводить (3).

Теорема2. Якщо послідовність функцій, неперервних на , збігається до граничної функції рівномірно на , то 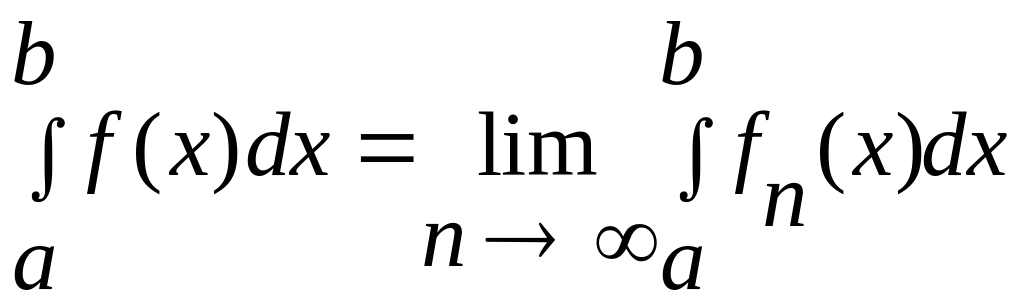. Цю рівність ще можна записати так: .

Теорема3. Нехай функції , визначені на і мають в ньому неперервні похідні . Якщо в цьому проміжку не тільки ряд (1), але і рівномірно збігається ряд, який складається із похідних: 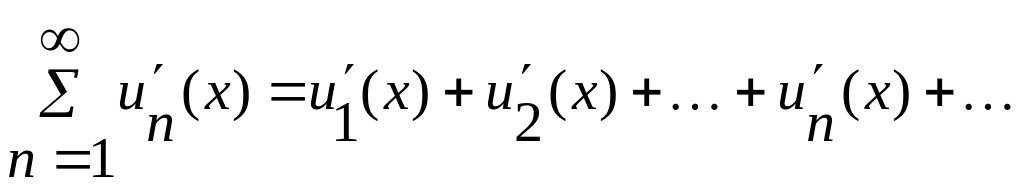(4), то і сума ряду (1) має на похідну, причому (5).

Доведен. Позначимо через суму ряду (4). Використовуючи теорему 1, про інтегруємо ряд (4) почленно від до , одержимо . , тоді . Так, як інтеграл зліва, з неперервності підінтегральної функції, має похідну рівну , то ту саму похідну має і функція , яка відрізняється від інтеграла на сталу. Рівність (5) можна переписати у вигляді: . Таким чином, похідна від суми ряду рівна сумі похідних ряду.

36. Ряд Тейлора. Розклад в ряд Тейлора

Означення. Степеневим рядом називається функціональний ряд

(*)

Члени якого є добутками сталих на степеневі ф-ї(з цілими показниками) від різниці (якщо ,то від самої змінної х).

Сталі називаються коефіцієнтами степеневого ряду.

Означення. Рядом Тейлора для ф-ї, Коли в певному околі точки ф-я має похідні до -го порядку включно, то:

в околі точки наз. степеневий ряд відносно різниці , коефіцієнти якого виражаються через похідні ф-ї у точці так:

Ці коефіцієнти наз. коефіцієнтами Тейлора ф-ї у точці .

Означення. Ф-я, яка в деякому інтервалі може бути подана своїм збіжним рядом Тейлора, наз. аналітичною в цьому інтервалі.

Степеневий ряд (*) наз. Рядом Тейлора.

Розглянемо декілька важливих прикладів розкладів ф-й в ряди Тейлора:

1. 

▲ Маємо

,

де , , . Отже,

, де .

Доведемо, що при . Числовий ряд з загальним членом (М-будь-яке число) збігається, в чому можна переконатися за ознакою Даламбера: . Значить, загальний член ряду повинен прямувати до нуля.

Отже, внаслідок довільності М ряд

Збігається до будь-якого х, тобто на всій осі Ох. Цей ряд наз. експоненціальним. ■

2)

3)

4)

5)

6)

37. Функція багатьох змінних. Границя, неперервність. Повторні і подвійні границі.

Нехай маємо змінних , спільні значення яких можуть вибиратися довільно із деякої множини точок - вимірного простору :ці змінні наз. незалежними. Якщо точку позначимо через , то функцію наз. Функцією цієї точки і позначають: . Нехай в деякій множині точок - вимірного простору задано функцій від змінних : (1).Припустимо, що якщо точка міняється в межах множини , то - вимірна точка , яка їй відповідає з координатами (1) не виходить за межі вимірної множини , де визначена функція - складена функція від незалежних змінних .

Арифметичні операції , які повторно застосовують до незалежних змінних , приводять до цілих многочленів таких виглядів:

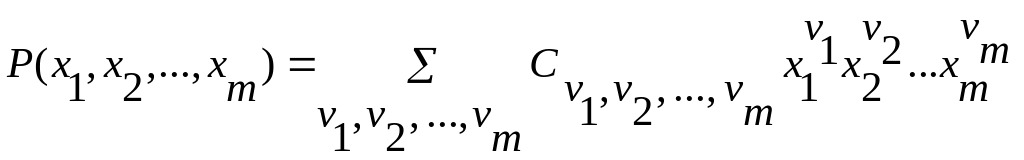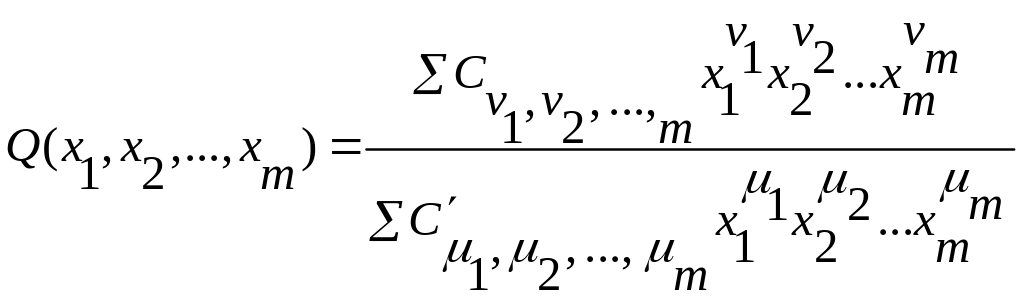і - це ціла раціональна і дробова раціональна функції.

Нехай точка - точка скупчення множини . Тоді із завжди можна виділити таку послідовність (1): 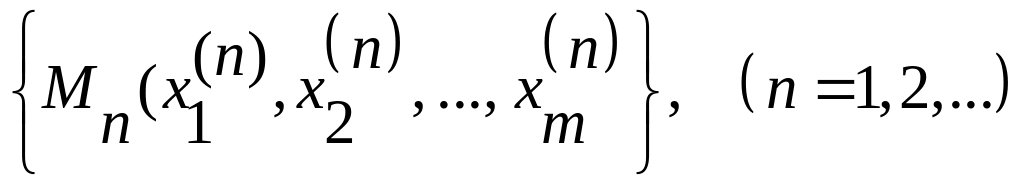, яка відрізняється від , яка б збігалася до .

Нехай в даній множині визначена функція . Тоді функція має своєю границею число при прямуванні змінних до , якщо яку б не виділити із послідовність (1) точок, відмінних від і збіжних до , числова послідовність , яка складається із відповідних значень функції, завжди збігається до . Позначають так: .

Сформулюємо дане означення “на мові ”: кажуть, що функція має своєю границею число , якщо для будь-якого числа існує таке число , що якщо , то .