28. Невласні інтеграли 1 і 2 роду. Критерій збіжності. Достатні умови

збіжності.

Критерій Коші збіжності невласного інтегралу першого роду:

, S(A) =

Критерій Коші збіжності невласного інтегралу другого роду:

збіжний

Абсолютна та умовна збіжність невласних інтегралів першого роду

(1)

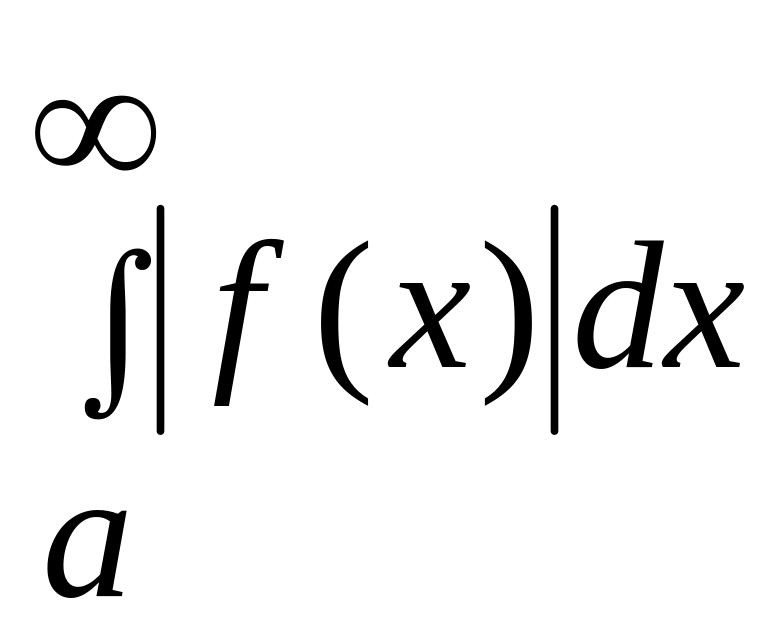(2)

Якщо збіжний (1) і збігається(2), то (1) - абсолютно збіжний, а f(x) абсолютно інтегровна.

(1) умовно збіжний (1) або (2).

Теорема: Якщо f(x) абсолютно інтегровна, (обмежена), .

Теорема: (1) абсолютно збіжний (2) збіжний.

Ä , Ä

Абсолютна та умовна збіжність невласних інтегралів другого роду

(3)

(4)

Якщо для збіжного (3) збігається(4), то (3) - абсолютно збіжний, а f(x) абсолютно інтегровна.

(3) умовно збіжний (3) або (4).

Ознаки Абеля та Діріхле для невласних інтегралів першого роду

( )

28. Невласні інтеграли 1 і 2 роду. Критерій збіжності. Достатні умови

збіжності.

Ознака Абеля: Якщо (збіжний), або g(x) , то ( ) збіжний.

Ä

= , Ä

Ознака Діріхле: Якщо S(A) = , то ( ) збіжний.

Ä

< , бо інтеграли обмежені, . Ä

Ознаки Абеля та Діріхле для невласних інтегралів другого роду

, b - особлива ( )

Ознака Абеля: Якщо (збіжний), або g(x) на [a,b), то ( ) збіжний хоча б умовно.

Ознака Діріхле: Якщо S( ) = , g(x) , то ( ) збіжний хоча б умовно.

29. Екстремум функції багатьох змінних. Необхідна умова. Достатні умови екстремуму

функції двох змінних.

Нехай функція визначена в області і внутрішня точка цієї області. Говорять, що функція в точці має максимум (мінімум), якщо її можна описати таким околом щоб для всіх точок цього околу виконувалась нерівність . Якщо цей окіл взяти настільки малим, щоб у кожній точці, крім самої точки виконувалась строга нерівність , то кажуть, що в точці має місце власний максимум(мінімум); в протилежному випадку максимум(мінімум) називається невласним.

Для позначення максимуму і мінімуму використовують загальний термін екстремум.

Припустимо, що дана функція в деякій точці має екстремум. Покажемо, що якщо в цій точці існують скінченні частинні похідні то всі ці частинні похідні дорівнюють нулю, так що перетворення в нуль частинних похідних першого порядку є необхідною умовою існування екстремуму.

Покладемо зберігаючи змінною. Тоді ми отримаємо функцію від даної змінної : Так як ми припустили, що в точці існує екстремум (нехай це буде максимум), то звідси випливає, що в деякому околі точки повинна виконуватись нерівність: так що функція в точці буде мати максимум, а звідси випливає, що Аналогічно показується, що в точці всі інші частинні похідні дорівнюють нулю.

Підозрілими на екстремум є точки, в яких всі частинні похідні першого порядку перетворюються в нуль. Їх координати можна знайти розв’язавши систему рівнянь: . Такі точки називаються стаціонарними.

Як і у випадку однієї змінної, в стаціонарній точці не обов’язково є екстремум. Тому розглянемо умови, достатні для існування екстремуму в стаціонарній точці.

Розглянемо випадок функції двох змінних Припустимо, що ця функція визначена, неперервна і має неперервні частинні похідні першого і другого порядків в околі деякої точки , яка є стаціонарною, тобто задовольняє умови:

Розглянемо різницю Розкладемо її за формулою Тейлора, обмежившись двома членами. Оскільки точка є стаціонарною, то перший член зникає, і ми отримаємо: . Роль відіграють різниці і всі похідні обчислені в деякій точці