Контрольная работа 2
Контрольная работа состоит из двух задач: в первой рассматриваются вопросы динамического исследования движения машинного агрегата; во второй проводится кинематический анализ зубчатого механизма.
Номер варианта задания или схемы соответствует последней цифре номера зачетной книжки студента, а вариант числовых данных соответствует предпоследней цифре номера зачетной книжки.
Задача 1
Вариант 1 (рис. 2, табл. 4). Двигатель 1 приводит в движение рабочую машину 2 посредством фрикционной муфты. Момент, развиваемый двигателем, зависит от угловой скорости его ротора и изменяется в соответствии с заданной механической характеристикой: МД = a – b1.
К
Рис.2. Схема
машинного агрегата с фрикционной муфтой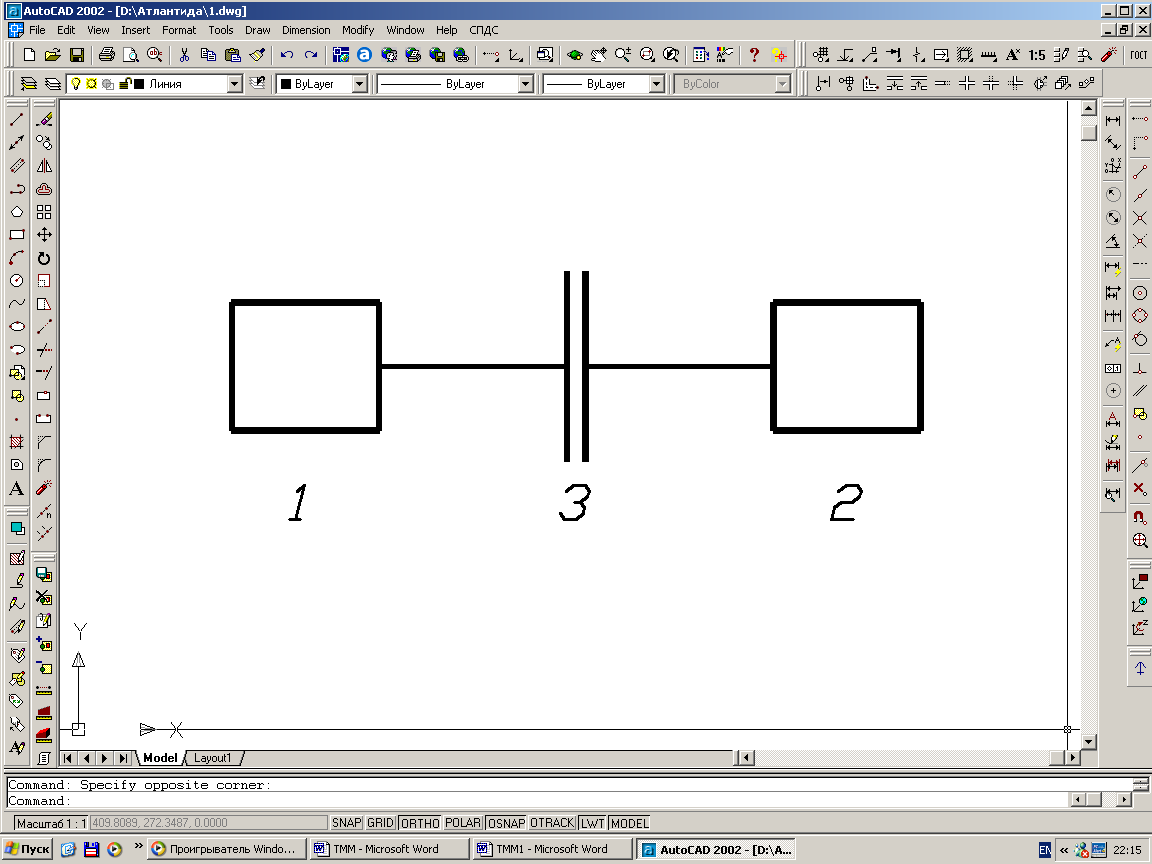
Решая дифференциальные уравнения движения ведущего и ведомого валов, выявить зависимость их скоростей 1 и 2 от времени. На одном графике построить функции 1(t) и 2(t) и по нему установить tс – время полного сцепления и определить общую скорость валов в момент полного сцепления. Выявить также закон изменения скорости всей системы 12 после полного сцепления муфты и определить скорость установившегося движения системы. Указанный график дополнить построением функции 12(t).
Таблица 4
Исходные данные к варианту 1
Параметры |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a, Нм |
2600 |
2100 |
1800 |
1000 |
1700 |
600 |
400 |
200 |
180 |
130 |
b, Нмc |
17 |
20 |
18 |
13 |
20 |
3,5 |
1,3 |
0,7 |
1,7 |
0,9 |
10, рад/с |
145 |
100 |
90 |
73 |
80 |
160 |
280 |
270 |
90 |
140 |
MТР, Нм |
1250 |
1200 |
850 |
400 |
750 |
370 |
160 |
120 |
100 |
100 |
MС, Нм |
400 |
450 |
300 |
170 |
220 |
150 |
140 |
40 |
30 |
40 |
Окончание табл. 4
Параметры |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
J1, кгм2 |
2,9 |
2,5 |
1,0 |
1,5 |
0,9 |
1,3 |
0,4 |
0,2 |
0,5 |
0,3 |
J2, кгм2 |
4,5 |
10 |
4,6 |
3,5 |
5,5 |
0,9 |
1,7 |
0,5 |
1,5 |
0,7 |
В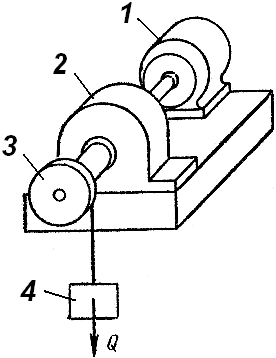
ариант
2 (рис. 3,
табл. 5). Электродвигатель
1
с
механической
характеристикой
Мд =
a
– b
через редуктор 2, передаточное отношение
которого равно ip,
приводит в движение из состояния покоя
барабан 3 лебедки.
Р
Рис. 3. Механизм
привода лебедки
Таблица 5
Исходные данные к варианту 2
Параметры |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Q, кН |
4 |
8 |
15 |
25 |
40 |
50 |
30 |
20 |
10 |
5 |
D, м |
0,2 |
0,25 |
0,28 |
0,3 |
0,35 |
0,5 |
0,4 |
0,4 |
0,3 |
0,25 |
h, м |
10 |
12 |
15 |
12 |
12 |
18 |
18 |
12 |
18 |
18 |
ip |
25 |
25 |
40 |
45 |
88 |
125 |
100 |
60 |
50 |
50 |
a, кНм |
0,2 |
0,38 |
0,7 |
1,0 |
0,75 |
2,0 |
1,0 |
1,01 |
0,45 |
0,25 |
b, Нмс |
2 |
2,5 |
7 |
6,6 |
5 |
13,3 |
10 |
10 |
3 |
2,5 |
Jб, кгм2 |
0,6 |
1,2 |
1,6 |
2,0 |
3,2 |
7,5 |
6,0 |
4,0 |
3,0 |
1,5 |
Jр, кгм2 |
0,01 |
0,02 |
0,07 |
0,07 |
0,15 |
0,19 |
0,19 |
0,17 |
0,17 |
0,05 |
Вариант 3 (табл. 6). Двигатель с механической характеристикой Мд = a – b приводит в движение вентилятор. Сопротивление вентилятора, приведенное к валу двигателя, задано соотношением Мc = c2 + f. Приведенный к валу двигателя момент инерции подвижных звеньев агрегата равен J. Определить зависимость скорости вала двигателя от времени (t) при пуске и выбеге агрегата. Вычислить скорость установившегося движения и время выбега. Построить в масштабе график (t).
Таблица 6
Исходные данные к варианту 3
Величина |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a, кНм |
2,6 |
2,1 |
1,8 |
1,7 |
1,0 |
0,6 |
0,4 |
0,2 |
0,2 |
0,15 |
b, Нмс |
17 |
20 |
17 |
22 |
13 |
3,6 |
1,3 |
0,67 |
1,7 |
0,8 |
c, мНмс2 |
290 |
1000 |
850 |
1350 |
790 |
110 |
20 |
10 |
850 |
26 |
f, Нм |
50 |
40 |
25 |
20 |
15 |
10 |
10 |
5 |
5 |
3 |
J, кгм2 |
5 |
12 |
5 |
6 |
5 |
1,2 |
2 |
0,7 |
2 |
1 |
Вариант 4 (табл. 7). Приближенно равномерное движение валика лентопротяжного механизма осуществляется пружинным двигателем, который снабжен центробежным тормозным регулятором скорости. Из состояния покоя валик разгоняется до угловой скорости р. После этого включается центробежный регулятор, вводящий дополнительное сопротивление и обеспечивающий тем самым приближенно равномерное движение рабочего валика.
Приведенный к рабочему валику момент инерции звеньев механизма J; приведенные к тому же валику момент сил, создаваемых пружинным двигателем, МД =a1–b1, момент сил сопротивления Мc =a2–b1, тормозной момент центробежного регулятора Мт = a2 – b. Решая дифференциальное уравнение движения рабочего валика, определить зависимость его скорости от времени (t) на интервале разгона и на интервале работы регулятора. Вычислить время разгона и скорость установившегося движения валика после включения регулятора. Построить график (t).
Таблица 7
Исходные данные к варианту 4
Величина |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
J, кгсм2 |
0,4 |
0,8 |
0,2 |
0,1 |
0,3 |
0,5 |
0,05 |
0,15 |
0,25 |
0,45 |
р, рад/с |
8 |
14 |
4,5 |
3,5 |
6,5 |
19 |
3,3 |
2,7 |
5,5 |
9,5 |
(a1 – a2), Нсм |
1,8 |
0,33 |
0,5 |
1,27 |
0,36 |
0,23 |
1,22 |
1 |
1,25 |
1,1 |
b, Нсм |
140 |
73 |
12,5 |
18,4 |
16,5 |
112 |
14 |
15 |
43,5 |
106 |
a, Нсмс2 |
1,8 |
0,33 |
0,5 |
1,27 |
0,36 |
0,29 |
1,22 |
1,7 |
1,25 |
1,1 |
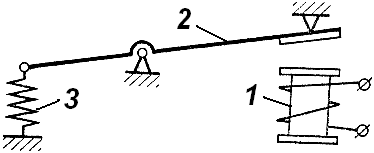
Вариант 5 (рис. 4, табл. 8). Для механизма электромагнитного реле, содержащего электромагнит 1, якорь 2 и возвратную пружину 3, определить время движения якоря после включения тока.
Рис. 4. Механизм электромагнитного реле |
омент
инерции якоря J;
угловой ход якоря m;
приведенный к якорю тяговый момент
электромагнита задан в виде М1
= a1
+ b1;
приведенный к якорю момент от силы
возвратной пружины М2 = a2 + b2. Искомое время определяется решением дифференциального уравнения движения якоря.
Построить график (t).
Таблица 8
Исходные данные к варианту 5
Величина |
Варианты числовых значений |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
J, кгсм2 |
100 |
90 |
70 |
70 |
60 |
50 |
40 |
30 |
20 |
10 |
|
m, рад |
0,1 |
0,2 |
0,15 |
0,15 |
0,2 |
0,1 |
0,1 |
0,2 |
0,15 |
0,1 |
|
a1, Нм |
0,5 |
0,3 |
0,25 |
0,44 |
0,3 |
0,4 |
0,2 |
0,6 |
0,15 |
0,2 |
|
b1, Нмрад-1 |
5 |
4 |
6 |
3 |
1,5 |
4 |
2 |
3 |
1 |
2,5 |
|
a2, Нм |
0,4 |
0,1 |
0,1 |
0,3 |
0,2 |
0,2 |
0,1 |
0,3 |
0,1 |
0,1 |
|
b2, Нмрад-1 |
3,7 |
3 |
5 |
2 |
1 |
2 |
1 |
1 |
0,7 |
1,5 |
|
|
|
||||||||||
Рис. 5. Подъемный механизм |
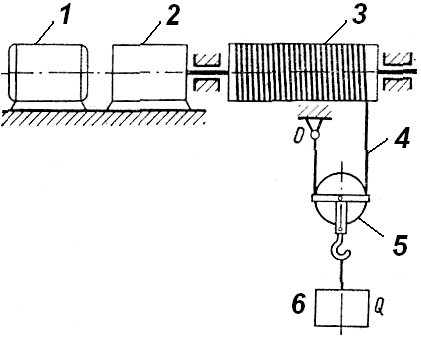
ариант
6 (рис. 5,
табл. 9).
Электродвигатель 1 через редуктор 2
приводит и движение из состояния покоя
барабан 3
подъемного
механизма. Канат 4, укрепленный на
барабане и в неподвижной точке O,
охватывает подвижный блок 5,
к обойме
которого на крюке подвешен поднимаемый
груз 6 весом Q.
В период пуска до достижения номинальной
скорости н
момент двигателя Мд1
= 1,2Mc,
где Mc
– момент от веса груза, приведенный к
валу двигателя. По достижении н
момент двигателя принимает значение
Мд2 =
Mc
и груз поднимается с постоянной скоростью.
Решая дифференциальные уравнения движения вала двигателя, определить время разгона двигателя до н и время подъема груза на высоту h. Рассчитать и построить диаграммы скорости и перемещения груза в зависимости от времени.
П
ередаточное
отношение редуктора iр,
диаметр барабана D, моменты инерции
барабана и ротора двигателя Jб
и
Jр.
Массой и толщиной каната пренебречь.
Таблица 9
Исходные данные к варианту 6
Величина |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Q, кН |
100 |
50 |
30 |
20 |
10 |
5 |
10 |
20 |
30 |
40 |
D, м |
0,5 |
0,4 |
0,4 |
0,3 |
0,2 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
h, м |
25 |
20 |
18 |
15 |
20 |
10 |
15 |
18 |
20 |
15 |
iр |
100 |
90 |
80 |
60 |
50 |
25 |
40 |
70 |
60 |
50 |
Jб, кгм2 |
8 |
6 |
4 |
3 |
2 |
1 |
1,5 |
2,5 |
3 |
5 |
Jр, кгм2 |
0,2 |
0,2 |
0,2 |
0,1 |
0,1 |
0,05 |
0,08 |
0,1 |
0,1 |
0,2 |
н, рад/с |
140 |
90 |
90 |
130 |
100 |
90 |
150 |
100 |
120 |
80 |
В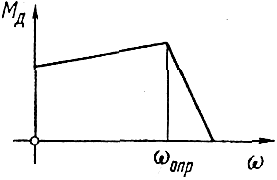
ариант
7 (рис. 6,
табл. 10).
Двигатель из состояния покоя приводит
в движение вал рабочей машины. Механическая
характеристика д
вигателя
состоит из двух прямолинейных участков:
Мд1
=
a1
+ b1
при 0опр
и
Мд2
=
a2
– b2
при опр.
Приведенный к валу двигателя момент
инерции вращающихся частей машины
и двигателя J,
момент сопротивления на том же валу
равен Mc.
Рис. 6. Механическая характеристика двигателя |
Таблица 10
Исходные данные к заданию 7
Величина |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a1, Нм |
96 |
94 |
55 |
45 |
38 |
24 |
13 |
11 |
7,5 |
7 |
b1, Нмс |
0,56 |
0,22 |
0,61 |
0,56 |
0,41 |
0,14 |
0,4 |
0,12 |
0,04 |
0,02 |
a2, кНм |
2,1 |
2,6 |
1,7 |
1,8 |
1,0 |
0,57 |
0,39 |
0,18 |
0,13 |
0,2 |
b2, Нмс |
20 |
17 |
22 |
17 |
13 |
3,6 |
1,3 |
1,7 |
0,8 |
0,7 |
J, кгм2 |
12 |
5 |
6 |
5 |
5 |
1,2 |
2 |
2 |
1 |
0,7 |
Mс, Нм |
60 |
67 |
50 |
40 |
35 |
20 |
10 |
10 |
7 |
6 |
Вариант 8 (рис. 7, табл. 11). Машинный агрегат состоит из двигателя 1, рабочей машины 2, зубчатого редуктора 4 и махового колеса 3. Момент двигателя Мд = a – b. Технологический цикл рабочей машины состоит из рабочего и холостого ходов. Моменты сопротивления, приложенные к валу машины при рабочем и холостом ходах, соответственно равны Mр и Mх. Продолжительность рабочего и холостого ходов tр и tх. Зубчатый редуктор 4 имеет передаточное отношение iр. Момент инерции ротора двигателя J1; момент инерции маховика и деталей, установленных на валу рабочей машины, J2.
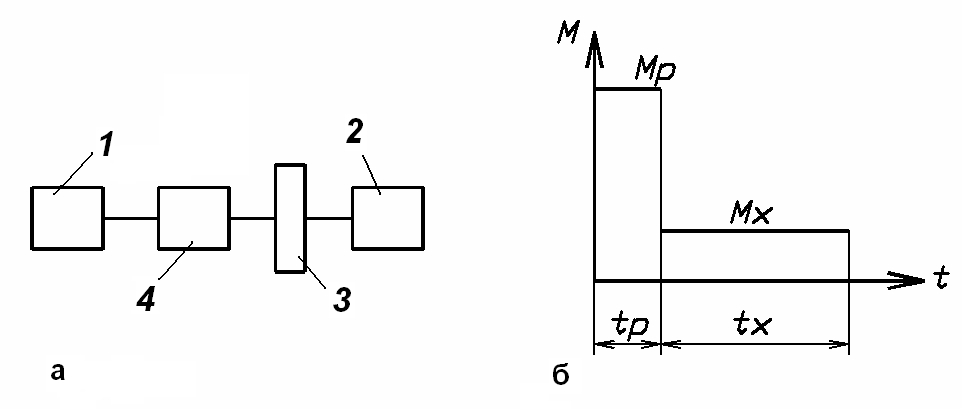
Рис. 7. Схема машинного агрегата (а) и диаграмма моментов сопротивления (б) |
Во время рабочего хода агрегата угловая скорость ротора двигателя уменьшается с величины макс до величины мин. При холостом ходе угловая скорость ротора двигателя возрастает от мин до макс. Приведя силы и массы к валу двигателя и решая дифференциальные уравнения движения вала двигателя при рабочем и холостом ходах агрегата, определить мин и tх. Рассчитать и построить в масштабе зависимости Mд(t), Mс(t) и (t). Вычислить коэффициент неравномерности хода .
Таблица 11
Исходные данные к варианту 8
Величина |
Варианты числовых значений |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Mр, кНм |
8 |
3 |
2 |
20 |
5 |
3,2 |
1,5 |
3 |
4 |
2,5 |
Mх, Нм |
200 |
50 |
80 |
400 |
150 |
0 |
0 |
0 |
0 |
0 |
J1, кгм2 |
0,4 |
0,4 |
1 |
1 |
0,5 |
0,1 |
0,1 |
0,1 |
0,2 |
0,3 |
J2, кгм2 |
480 |
120 |
200 |
500 |
250 |
200 |
250 |
200 |
220 |
750 |
ip |
4 |
5 |
4 |
4 |
5 |
4 |
5 |
5 |
4 |
5 |
a, кНм |
10 |
1 |
1,5 |
30 |
3 |
3 |
2 |
3 |
6 |
5 |
b, Нмс |
100 |
10 |
10 |
200 |
20 |
30 |
20 |
20 |
40 |
50 |
tр, с |
0,2 |
0,1 |
0,6 |
0,3 |
0,5 |
0,2 |
0,4 |
0,5 |
0,3 |
0,5 |
макс, рад/с |
99 |
98 |
146 |
148 |
147 |
99 |
99 |
148 |
148 |
99 |
Вариант 9 (табл. 12). На вал рабочей машины, имеющей приведенный момент инерции J и вращающийся с угловой скоростью y, с некоторого момента времени начинает действовать тормозной момент, зависящий от времени: Mт= at. Под действием этого момента рабочая машина, двигатель которой выключен, будет совершать выбег.
Решая дифференциальное уравнение вращения вала при выбеге, выявить зависимость его угловой скорости от времени (t); определить также зависимость от времени углового ускорения (t) и зависимость угла поворота вала от времени (t). Определить время выбега и число оборотов вала за время выбега. Построить графики (t), (t) и (t).
Таблица 12
Исходные данные к варианту 9
Величина |
Варианты числовых значений |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
J, кгм2 |
5 |
4,4 |
4 |
3,7 |
1,6 |
1,5 |
1,2 |
1 |
0,5 |
0,2 |
y, рад/с |
74 |
152 |
300 |
75 |
102 |
100 |
103 |
156 |
150 |
310 |
a, Нм/с |
300 |
130 |
60 |
100 |
18 |
25 |
80 |
100 |
15 |
10 |
Вариант 10 (рис. 8, табл. 13). Машинный агрегат состоит из двигателя 1, рабочей машины 2, зубчатого редуктора 3 и маховика 4. Момент, развиваемый двигателем, определяется соотношением Мд = a – b.
Технологический цикл рабочей машины состоит из рабочего и холостого ходов, продолжительность которых соответственно tр и tх. Моменты сопротивления, приложенные к валу машины при рабочем и холостом ходах, равны Mр и Mх. Передаточное отношение редуктора равно ip. Момент инерции вала двигателя J1, момент инерции деталей, установленных на валу рабочей машины, J2.
За время рабочего хода агрегата угловая скорость вала двигателя уменьшается с величины макс до величины мин. Колебание угловой скорости вала двигателя при рабочем ходе в заданных пределах обеспечивается установкой маховика 4 с моментом инерции Jм. При холостом ходе угловая скорость вала двигателя возрастает от мин до макс.
Приведя силы и массы к валу двигателя и решая дифференциальные уравнения движения вала двигателя при рабочем и холостом ходах агрегата, определить Jм и tх. Рассчитать и построить в масштабе зависимости Mд(t), Mс(t) и (t).
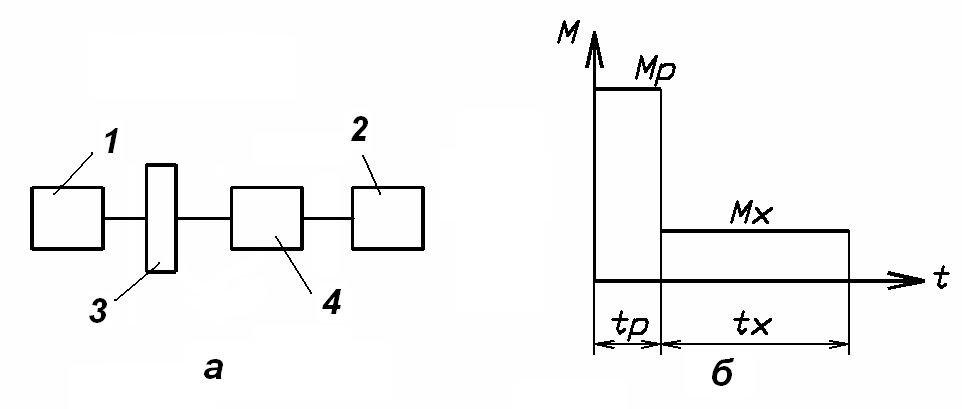
Рис. 8. Схема машинного агрегата (а) и диаграмма моментов сопротивления (б) |
Таблица 13
Исходные данные к варианту 10
Величина |
Варианты числовых значений |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Mр, кНм |
2,5 |
4 |
3 |
1,5 |
1,2 |
3 |
10 |
1,6 |
1 |
4 |
Mх, кНм |
0,5 |
0,8 |
0,5 |
0,3 |
0,2 |
0,5 |
2 |
0,3 |
0,2 |
0,8 |
J1, кгм2 |
0,3 |
0,2 |
0,1 |
0,1 |
0,2 |
0,5 |
1 |
1 |
0,4 |
0,4 |
J2, кгм2 |
10 |
8 |
7,5 |
5 |
6 |
10 |
16 |
8 |
5 |
6,4 |
ip |
5 |
4 |
5 |
5 |
4 |
5 |
4 |
4 |
5 |
4 |
Величина |
Варианты числовых значений |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Окончание табл.13
a, кНм |
5 |
6 |
3 |
2 |
3 |
3 |
30 |
1,5 |
1 |
10 |
b, Нмс |
50 |
40 |
20 |
20 |
30 |
20 |
200 |
10 |
10 |
100 |
tр, с |
0,5 |
0,3 |
0,5 |
0,4 |
0,2 |
0,5 |
0,3 |
0,6 |
0,1 |
0,2 |
макс, рад/с |
99 |
148 |
148 |
99 |
99 |
147 |
148 |
146 |
98 |
99 |
мин, рад/с |
94 |
135 |
130 |
92 |
90 |
120 |
130 |
130 |
88 |
90 |