6.11. Робота з матрицями
В математиці, набір значень, упорядкований у вигляді рядків і стовпців, називається матрицею, наприклад:
Рис. 6.22. Матриця А [3х3]
Матриця – сукупність чисел, розміщених у прямокутній таблиці у вигляді m рядків і n стовпців. Якщо m=n, то матрицю називають квадратною, порядку n.
Матриця, яка складається з одного рядка або одного стовпця називається вектором.
Електронні таблиці представляють собою природне середовище для роботи з матрицями, оскільки в їх комірках зручно розташовувати матричні елементи.
Ці об’єкти в MS Excel розглядаються як масиви чисел. Матриці можна перемножувати між собою, множити на вектор, транспонувати, створювати обернені матриці тощо. Хоча в MS Excel і надає можливість для виконання будь-якої стандартної матричної операції, однак виконуються ці операції по-різному:
додавання двох матриць та множення матриці на скаляр здійснюється за допомогою звичайних арифметичних функцій, котрі здійснюють операції з умістом комірок;
транспонування, перемноження і обернення матриць виконується за допомогою вбудованих функцій масивів.
6.12. Додавання двох матриць
Додавання матриць можна здійснити тільки при умові, що матриці мають однаковий розмір. Наприклад, прибавимо дві матриці, зображені на рис. 6.23.
Рис. 6.23. Матриця А [3х3] і матриця В [3х3] Рис. 6.24. Додавання двох матриць (крок 1)
Щоб додати одну матрицю до іншої, потрібно додати один до одного всі їх відповідні елементи. Наприклад, у верхній лівій комірці результуючої матриці буде міститись формула для додавання вмісту комірок В4 і В8 (1+4). Формула запишеться як: =В4+В8. Введемо цю формулу в комірку В12 і отримаємо результат (рис. 9.24).
Якщо тепер скопіювати вміст комірки В12 в діапазон В12:С14, Excel поелементно додасть матрицю А до матриці В.
Рис. 9.25. Додавання двох матриць (крок 2)
6.13. Множення матриці на скаляр
Введемо в електронну таблицю скаляр і матрицю, яку потрібно на нього помножити. Скаляр – величина, яка повністю визначається своїм числовим значенням. Щоб помножити матрицю на скаляр, потрібно помножити на скаляр кожний елемент цієї матриці.
Наприклад, треба помножити матрицю А на число 3. Для цього виділяють область вільних комірок розміром, що відповідає заданій матриці, наприклад D2:F4 (рис. 6.26).
Рис. 9.26. Виділення діапазону для множення матриці А на скаляр
Далі у рядку формул вводять формулу: =А2:С4*3 і натискують на сукупність клавіш <Сtrl+Shift+Еnter>. У виділеному діапазоні комірок з'являться значення даних, які помножені на число 3 (рис. 6.27).
Рис. 6.27. Результат множення матриці А на скаляр
6.14. Множення двох матриць
Дві матриці можна перемножити тільки при умові, що кількість стовпців першої матриці дорівнює кількості рядків другої матриці.
Вектор – величина, що характеризується розміром і напрямком.
Нехай, наприклад, треба помножити матрицю на вектор. Для цього використовують функцію МУМНОЖ (Массив1; Массив2), де Массив1, Массив2 – це масиви, які перемножуються. Кількість стовпців аргументу Массив1 має бути такою, як і кількість рядків аргументу Массив2. Результатом множення матриць є масив з такою самою кількістю рядків, що й масив 1, і з такою самою кількістю стовпців, що и масив 2. Множення матриць здійснюється за формулою:
bij=
aij
·
ckj,
де: b – елемент нового масиву;
i – номер рядка;
j – номер стовпця;
аik – елемент масиву 1;
сkj – елемент масиву 2;
k – номер рядка масиву 1 або номер стовпця масиву 2;
n – розмір матриці.
При множенні матриці на вектор, розрахована матриця має розмірність вектора. Спочатку створюють вектор С у діапазоні G2:G4(рис. 6.28),
Рис. 6.28. Вектор С
який повинен мати стільки рядків, скільки стовпців є в матриці А2:С4(рис. 6.29).
Рис. 6.29. Матриця А
Далі виділяють діапазон комірок, де буде створюватися нова матриця (А7:А9), активізують кнопку „Вставка функции”, вибирають функцію МУМНОЖ, і заносять відповідні значення діапазонів матриці А та вектора С (рис. 6.30).
Після цього встановлюють курсор на рядок формул, натискують на клавіші <Сtrl+Shift+Еnter> й одержують результат, представлений на рис. 6.30.
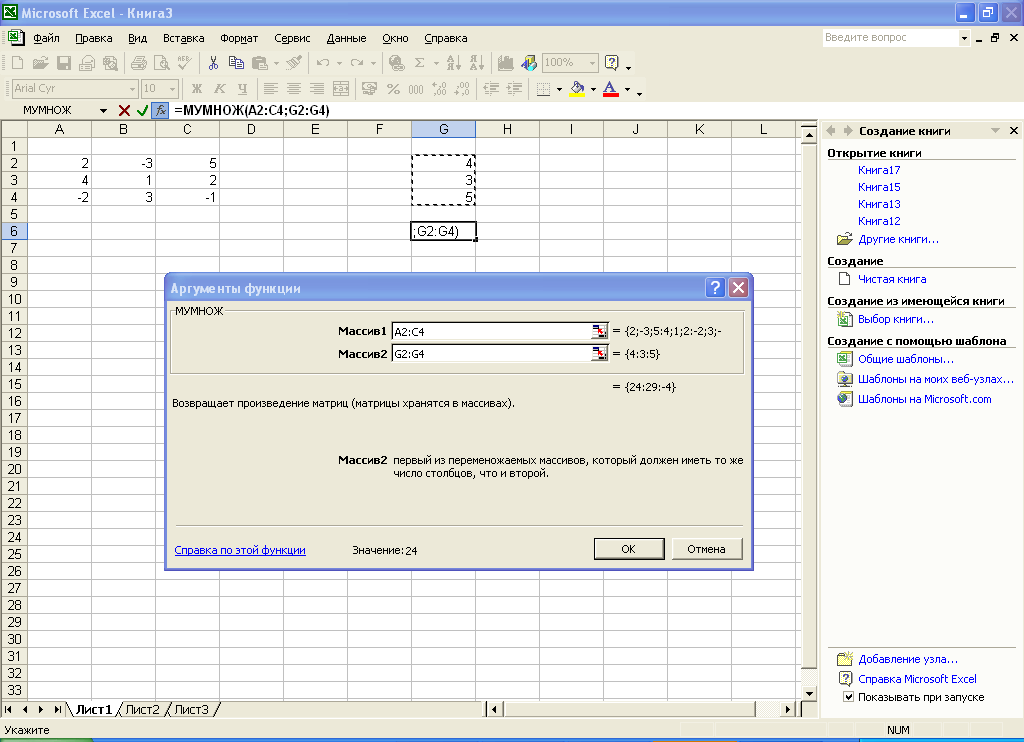
Рис. 6.30. Множення матриці на вектор