Описание установки

Приборы для измерения линейного расширения при нагревании тел называются дилатометрами. Трудность измерения коэффициентов линейного расширения заключается в том, что их величина мала (α ≈ 10^-6).Кроме того, при нагревании расширяются элементы из­мерительной системы, что значительно усложняет конструкции дилатометров. Используются различные методы регистрации линейного расширения:

– механические,

– оптические, включая интерференционные,

– фотометрические,

– емкостные и др.

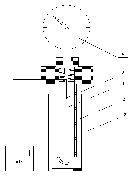
Рис.2

В данной лабораторной работе используется дилатометр с регистрацией теплового расши­рения механическим стрелочным индикатором перемещений. Схема дилатометра приведена на рис.2. Исследуемый образец 1, помещенный в кварцевую трубку 2, вносится в электрическую печь 3 для нагревания. Одним концом образец опирается на дно запаянной кварцевой трубки, другим – через кварцевый стержень связан с толкателем стрелочного индикатора 4. Использование в измерительных цепях дилатометра кварцевых элементов в силу малого теп­лового расширения кварца позволяет свести к минимуму систематические погрешности изме­рений. При нагревании образец расширяется, увеличение его линейных размеров измеряется стрелочным индикатором. Цена минимального деления шкалы индикатора обозначена на его лимбе. Температура образца измеря­ется с помощью термопары 5.

Порядок проведения измерений

1. Поместить кварцевую трубку с образцом в электрическую печь.

2. В заданном интервале температур одновременно снимать показания стрелочного индикатора Δl и показания милливольтметра термопары.

3. Результаты измерений занести в разработанную таблицу.

Обработка результатов измерений

1. Используя градуировочную таблицу термопары, перевести показания милливольтметра в температуру и построить точечную зависимость Δl = f(ΔT).

2. В заданном интервале температур методом наименьших квадратов (МНК) рассчитать угловой коэффициент dl/dT и построить график Δl = f(ΔT).

3. Для оценки дисперсии экспериментальных точек рассчитать коэффициент корреляции r.

4. По формуле (2) рассчитать среднее значение коэффициента теплового расширения в заданном интервале температур и сравнить его с табличным.

Лабораторная работа № 6.5

УПРУГИЕ ХАРАКТЕРИСТИКИ

МЕТАЛЛОВ И СПЛАВОВ

Цель работы: экспериментальное определение упругих характеристик поликристаллических металлов и сплавов.

Введение

Упругие характеристики описывают способность металлов и сплавов обратимо изменять размеры и форму под действием нагрузок, т.е. упруго деформироваться.

В общем случае деформации могут быть достаточно сложными (изгиб, кручение и др.), но во всех случаях они сводятся к суперпозиции простейших видов: линейное растяже­ние (сжатие), простой сдвиг и деформация всестороннего сжатия.

Простые деформации подчиняются также простым законам, связывающим напряжения и деформации линейно (законы Гука):

σ_n = Еε_p ,

σ_t = Gε_t, (1)

p = Kε_v ,

где σ_n – нормальные напряжения при деформации растяжения(сжатия); σ_t – касательные напряжения при простом сдвиге; р – давление всестороннего сжатия; ε_p – деформация при линейном растяжении(сжатии); ε_t – деформация сдвига; ε_v = ΔV/V – объемная деформация при всестороннем сжатии; E,G, К – модули Юнга, сдвига и всестороннего сжатия.

В случае сложных деформаций σ и ε являются тензорными величинами – соответст­венно σ_ij и ε_kl. В этом случае также выполняется линейная зависимость, но между тензором напряжений и тензором деформацией

σ_ij ~ ε _kl . (2)

Соотношение (2) в виде равенства

σ_ij = C _ijkl · ε _kl (i,j,k,l = 1,2,3) (3)

называют законом Гука в обобщенной форме, где C _ijkl – тензор модулей упругости. В силу симметричности тензоров σ_ij, ε_kl и C_ijkl закон Гука может быть свернут по парам индексов и запи­сан в другой, матричной форме:

σ_i = C_ik· ε _k (i,k = 1,2,3,4,5,6). (4)

Для изотропных тел (в том числе для поликристаллов) независимыми являются только два модуля упругости С₁₁ и С₁₂ (здесь использовано матричное обозначение моду­лей: С₁₁= С₁₁₁₁, С₁₂ = С₁₁₂₂). Из них можно сформировать некоторые линейные комбинации, имеющие простой физический смысл:

модуль сдвига G = (С₁₁ – С₁₂)/2, (5)

модуль всестороннего сжатия K = (С₁₁ + 2С₁₂)/3. (6)

Комбинации G и K дают:

модуль Юнга E = 9KG/(3K+G), (7)

коэффициент Пуассона ν = (3K-2G)/2(3K+G). (8)

Наиболее употребительными характеристиками упругих свойств поликристаллических ме­таллов и сплавов являются E, G, K и ν, называемые техническими характеристиками. Однако независимых характеристик только две, так как в основе их определения лежат комбинации двух модулей упругости С₁₁ и С₁₂. Поэтому технические характеристики связаны между собой определенными соотношениями, кроме приведенных выше (7,8):

E = 2G(1 + ν), (9)

K = . (10)

Упругие характеристики сплавов зависят от состава сплава, термической обработки, наличия и валентности примесных атомов. Некоторые закономерности этих зависимо­стей установлены. Например, в бинарных твердых растворах имеет место аддитивная зависимость модуля Юнга от атомной концентрации второй фазы с_ат:

Е = (1 – с_ат) Е₁ + с_атЕ₂ = Е₁ + (Е₂ – Е₁)с_ат . (11)

Для бинарных гетерогенных смесей имеет место аддитивная зависимость модуля Юнга от объемной концентрации второй фазы с_об:

Е = (1 – с_об) Е₁ + с_обЕ₂ = Е₁ + (Е₂ – Е₁)с_об . (12)